线性时变时滞系统稳定性的新判据
程璐华,张宝琳
(中国计量大学 理学院,浙江 杭州 310018)
实际系统中,时滞的存在通常会导致系统性能变差甚至不稳定,因此时滞系统稳定性分析问题一直是控制领域的热点研究课题之一。研究时滞系统的稳定性问题,主要目的在于得到可允许的时滞上界以保证系统的稳定性。通过构造合适的Lyapunov-Krasovskii泛函并估计该泛函沿着系统关于时间导数的上界,进而得到时滞系统具有较小保守性的渐近稳定性判据是时滞系统稳定性研究的时域方法之一[1-3]。例如,文献[4]和[5]中,通过在构造的增广Lyapunov-Krasovskii泛函中引入更多的时滞信息,降低了系统稳定性判据的保守性;为估计Lyapunov-Krasovskii泛函导数中的积分项,自由权矩阵方法[6,7]、积分不等式方法[8,9]、Wirtinger积分不等式法[10]以及Bessel-Legendre不等式法[11]得到了深入的研究。最近,文献[12-14]研究了基于二重积分不等式方法和三重积分不等式方法得到了时变时滞系统稳定性的新判据。事实上,不难发现,现有的结果,例如文献[14]提出的三重积分不等式方法以及基于此得到的时滞系统稳定性判据仍然存在一定程度的保守性,有进一步改进的空间。
本文针对一类含有时变时滞的线性系统,研究系统的稳定性新判据。首先给出了一个新三重积分不等式,改进了文献[15]中的对应结果;进而通过构造Lyapunov-Krasovskii泛函,采用新得到的三重积分不等式估计Lyapunov-Krasovskii泛函导数项中的三重积分项,并结合凸组合方法得到了时滞系统稳定性的新判据。最后通过一个数值实例,验证了方法的有效性和优越性。
在本文中,diag{…}表示对角矩阵;col{…}表示列向量;Rn表示n-维欧几里得空间;He{A}表示A+AT;“*”表示对称矩阵中的对称项。
1 问题描述
考虑一类含有时变时滞的线性系统
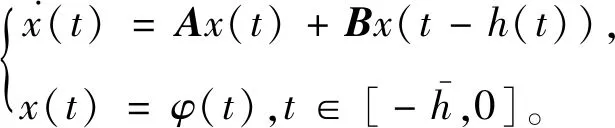
(1)
其中,x(t)∈Rn为系统状态向量,A,B为合适维数的系统矩阵,h(t)为系统时变时滞,满足
(2)
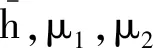
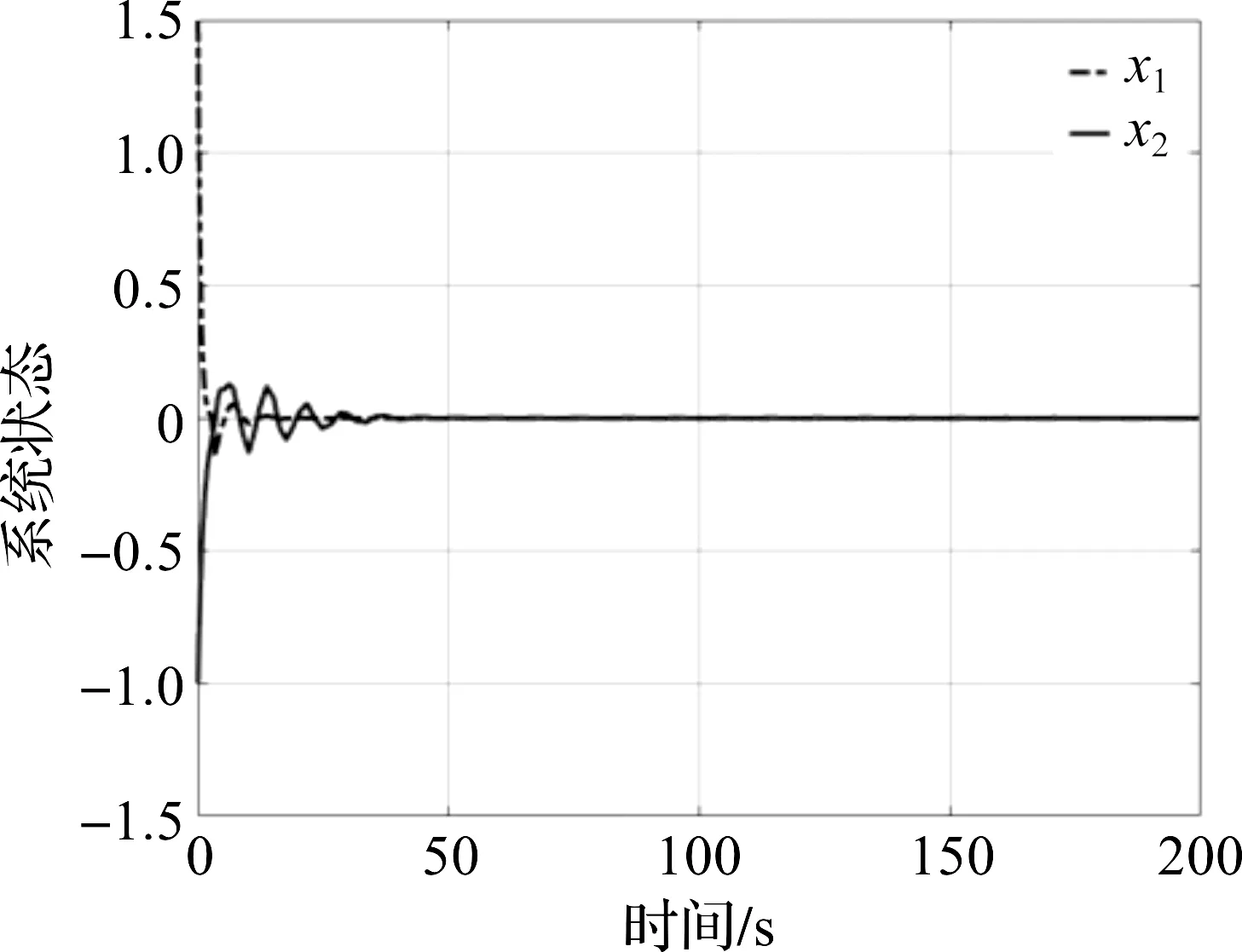
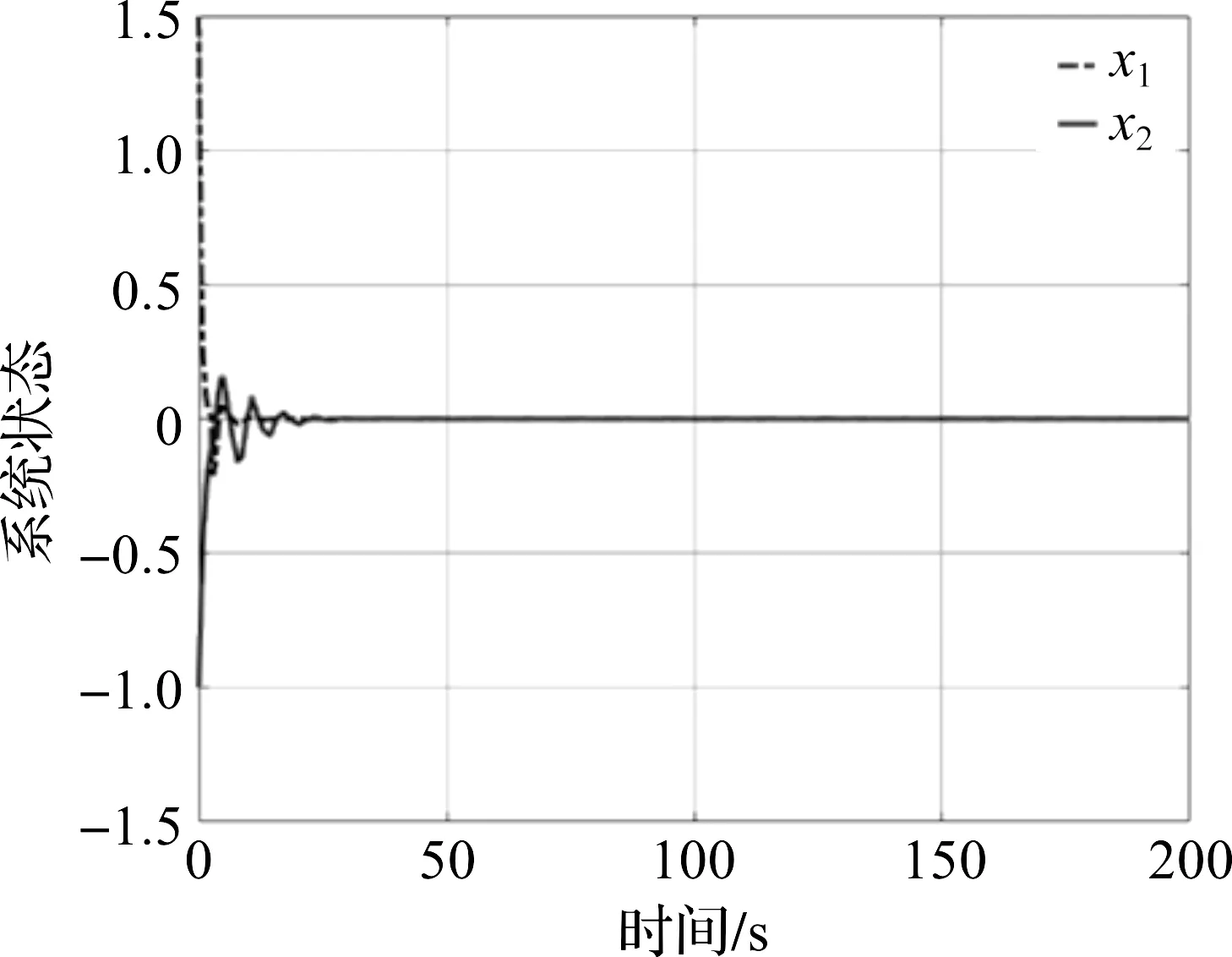
引理1[10]:对于n×n实常数矩阵R>0,适当维数的实矩阵M,标量a和b,且a (3) 其中R=diag{R,3R,5R},且 (4) 引理2[11]:对于n×n实常数矩阵R>0,标量a和b,且a 则下面不等式成立: (5) 其中 (6) 引理3[12]:对于n×n实常数矩阵R>0,标量a和b,且a (7) 引理4[15]:对于n×n的实对称矩阵R>0,标量a和b,且a (8) 其中,v1和v2的定义见式(6)。 引理5:对于n×n实常数矩阵R>0,标量a和b,且a (9) 其中,v1、v2和v3的定义见(6)式。 进而,根据引理3可得 (10) 其中 注意到 (11) 以及 (12) 从而,可得 (13) 将(11)—(13)代入(10),并注意到(6),可直接得到(9)。引理5证毕。 (14) 令: (15) (16) 其中,矩阵P1>0,P2>0为待求矩阵,wi(t)(i=1,2,3,4)如下定义: 构造如下形式的Lyapunov-Krasovskii泛函: V(t,xt)=V1(t,xt)+V2(t,xt)+V3(t,xt), 其中: V1(t,xt)=χT(t)P(h(t))χ(t), 为简化起见,令 (17) 其中,0和I分别为n×n零矩阵和n×n单位矩阵。于是,由(16)和(17),可得: (18) 从而,系统(1)可表示为 (19) 其中 C0=Ae1+Be2。 由式(15)及(18)可得 (20) 其中: C12=col{0,0,0,e6,e7,-e4,-e5}; 下面给出时滞系统(1)渐近稳定的一个充分条件。 (21) (22) 其中: (23) (24) (25) (26) 其中: (27) (28) (29) (30) 其中,C311=col{e2,e3,e4,e5},C312=col{e1,e2,e6,e7}。 证明:令: (31) 及 对V(t,xt)沿系统(1)关于时间t求导,可得 其中, (32) (33) (34) 由式(18),(31)及(32)可得 (35) 根据式(19)及(29)可得 (36) 进而,由式(33)~(36),可得 (37) (38) (39) 其中,Θ由式(4)给出。 进而,由(38)和(39)可得 (40) 其中,Φ312由式(29)给出 (41) 于是, 2(t)≤ξT(t)Φ33ξ(t)。 (42) 其中,Φ33由式(30)给出。 进而,有 (43) 由式(37),(40),(42)和(43)可得 为保证系统渐近稳定,需要下面不等式成立: (44) (45) 根据引理5,如果不等式 (46) 根据Schur补,式(46)等价于 根据引理6,已知条件(22)保证了不等式(23),(24)和(25)成立,亦即式(44)成立,进而,有 从而系统渐近稳定。定理得证。 例.考虑系统(1),系统参数如下: Table 1 Maximum upper bounds of system delay 图1 h(t)=4.843+0.1sin(t)的系统状态曲线Figure 1 State curves of time-delay system with h(t)=4.843+0.1sin(t) 图2 h(t)=2.808+0.5sin(t)的系统状态曲线Figure 2 State curves of time-delay system with h(t)=2.808+0.5sin(t) 图3 h(t)=2.077+0.8sin(t)的系统状态曲线Figure 3 State curves of time-delay system with h(t)=2.077+0.8sin(t) 本文针对一类具有时变时滞的线性系统,研究了系统的渐近稳定性问题。首先,得到了一个具有更小上界的新的三重积分不等式,并基于改进的三重积分不等式和凸组合方法,利用新构造的Lyapunov-Krasovskii泛函,得到了时滞系统渐近稳定的时滞相关稳定性新判据,该稳定性判据具有更小的保守性。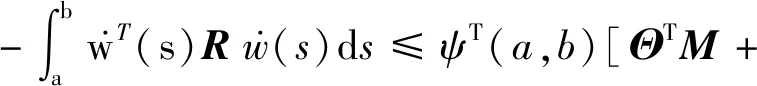
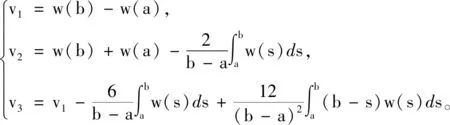
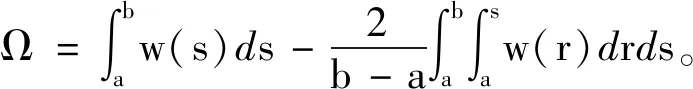


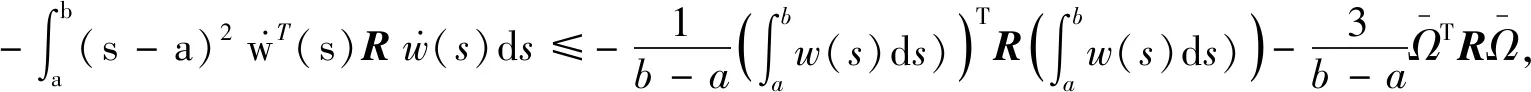


2 稳定性判据

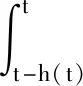
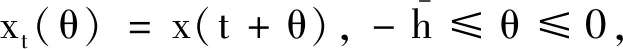
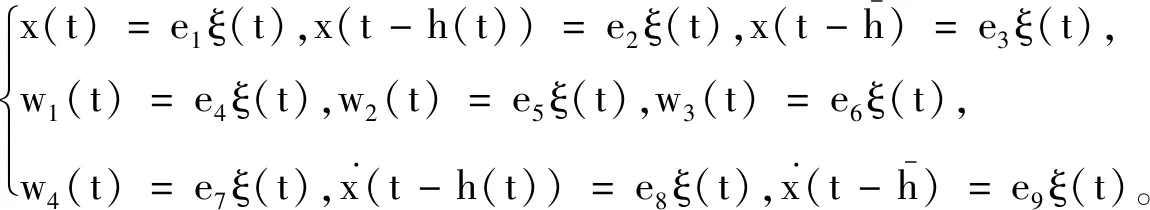
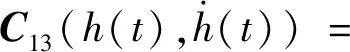


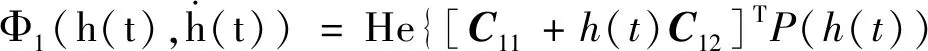

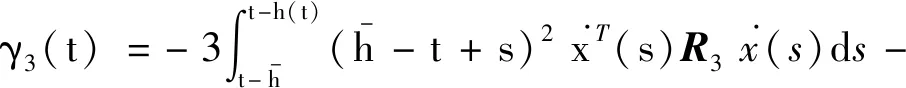
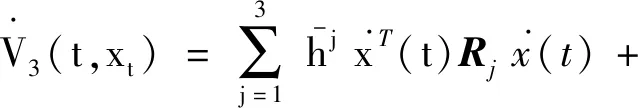
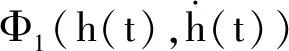

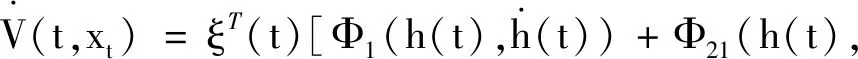

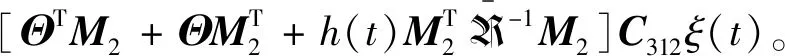


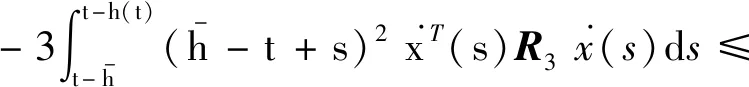
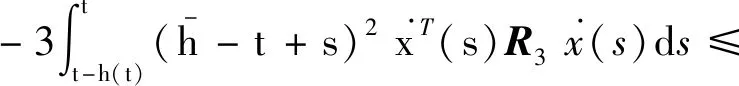
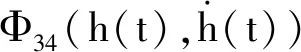
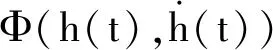
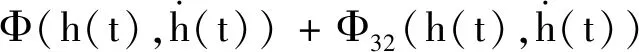

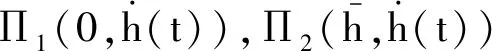

3 数值实例


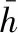


4 结 论

