基于群体可拓模糊理论的地铁运营火灾风险评估

谢妤倩，刘 辉，牟 杰，王智文，单江梁，游温娇，孔凡玉

(1.中国计量大学 质量与安全工程学院，浙江 杭州 310018； 2.浙江省安全生产科学研究院，浙江 杭州 310011； 3.杭州佳宁安全科技有限公司，浙江 杭州 311100)

近年来我国城镇化速度加快，城市人口数量不断增大，许多大中城市交通拥堵问题日趋严重。地铁以其运量大、速度快、耗能少和污染小的特点，被广泛应用于大中城市以缓解交通压力。由于地铁在密闭空间运行，一旦发生火灾，其事故后果往往比较严重[1]。许多因素可引起地铁火灾，如电气设备故障、工作人员违章操作、列车运行产生的电弧、鼠害等。另外，地铁运营空间特点使得应急管理与救援有一定难度。

早在20世纪60年末，我国北京地铁就因内燃机车电器故障引发特大火灾，导致8人死亡，300多人受伤，直接损失100多万元。2015年11月，上海地铁大木桥站设备故障导致电缆垃圾着火，使近七万人出行受到影响。国外同样遭遇火灾危害：2003年2月，韩国大邱地铁发生人为纵火事件，造成198人死亡147人受伤；2013年6月，俄罗斯莫斯科“猎队”地铁站因高压线破损燃烧发生火灾，造成11人重伤；2015年1月，美国华盛顿兰芳广场站一地铁车厢突然起火并冒出浓烟，导致1人死亡2人重伤，80多人入院治疗。这些事故表明，地铁一旦发生火灾，后果可能极其严重，因此地铁火灾隐患不容忽视，应当引起社会重视和学者的关注。

在地铁运营火灾风险评估研究的领域中，许多国外学者从烟气角度研究地铁火灾风险，如GIACHETTI等[2]对地铁站烟气扩散进行实验研究，确定了最佳的通风策略；ROH等[3，4]运用火灾模拟和疏散模拟，证明了站台屏蔽门和通风系统有利于控制烟气的扩散，延长了疏散的可用时间；VITTORI[5]利用数值分析评估了紧急通风系统控制烟尘传播的能力。国内学者也做了相关研究，WANG[6]通过比较FLUENT和FDS对地铁站台火灾烟气传播的模拟结果，为其烟气传播研究提供参考；MENG等[7]通过仿真模拟探究了地铁车厢起火时不同通风方式的有效性，为地铁车厢着火时的烟气控制设计提供参考。然而大多数国内学者是基于神经网络、层次分析法、模糊理论或可拓理论展开地铁运营火灾风险评估。如喻茗之[8]、李江华[9]运用神经网络建立了地铁(站)火灾风险评价模型；HUANG[10]和GAO[11]使用模糊层次分析法评估了地铁火灾风险；许贵贤[12]从“人、设备、环境、管理”四方面构建了地铁火灾危险性模糊评价模型，陈曼英[13]从“风险源、人、管理、环境”四方面建立了地铁车站火灾风险的模糊综合评价模型；阳富强[14]、于恒[15]则结合了可拓理论评价地铁火灾风险。以上方法中，层次分析法主观性较强，而模糊层次分析法则常用于分析不矛盾问题；对于模糊综合评价法，其结果往往只由若干个因素决定，准确性还有待提高[16]。可拓理论则善于解决矛盾性问题，能以定性与定量相结合的方式对较为复杂、不易描述的问题进行分析，多运用于存在不确定性和矛盾的复杂系统[17]。

由于火灾风险是一个多因素、多层次的复杂体系。而地铁站人员集中，地铁运营本身也是一个复杂系统，既可能存在不确定性，还可能兼具矛盾性。因此本文参考标准《城市轨道交通运营线路安全评价规范》建立地铁火灾风险评估体系，与可拓学理论结合，利用模糊数学方法计算专家打分，从而计算出各级评估指标的权重；并以N市某地铁站为例，利用可拓学方法对其火灾风险进行物元可拓评估定级，为预防地铁火灾和应急管理提供科学依据。

1 群体可拓模糊理论方法

1.1 理论基础

群体可拓模糊理论是群决策理论、可拓理论和模糊数学方法的集合。群决策理论是指以群体为决策主体所进行的决策活动，包括德尔菲法、头脑风暴法、思路转换法和异地思考法[18]，本文采用德尔菲法。可拓理论(Extension Theory)最早由广东工业大学的蔡文研究员提出，其主要理论包括基元理论、可拓集合理论和可拓逻辑，有助于不确定性问题和矛盾问题的评估[17]。模糊数学(Fuzzy数学)是研究和处理模糊性现象的一种数学理论和方法，能在承认数学精确性的同时向模糊性逼近[19]。

1.2 群体可拓模糊理论评估模型

群体可拓模糊评估模型既能解决地铁系统的不确定性问题和矛盾问题，又能增加评估的科学性和准确性。

1.2.1 确定评价物元

根据已确定的地铁运营火灾风险评估体系，设需要评价的对象有m种，评价对象对应的指标有n个，则地铁火灾风险评估可用下面的n维物元描述：

(1)

式(1)中：R为地铁运营火灾风险评估的物元，其中，Ni(i=1,2,…,m)为第i种待评对象，ck(k=1,2,…,n)为该评价对象对应的第k个指标；uik为第i种地铁运营火灾风险评估对象对应于其影响指标k的取值范围。

1.2.2 确定经典域和节域

经典域物元Roj(第j个指标的经典域物元)

(2)

节域Rp

(3)

1.2.3 确定待评价物元

确定待测物元Rm

(4)

1.2.4 确定各指标权重

向专家团队发放问卷，采用1-9标度法表示与某上层因素z关联的n个因素的相对重要度。设与上层因素z关联的n个因素为x1，x2，…xn，其中，i,j=1，2，…，n，以aij表示第i个指标关于第j个指标的重要度，且aii=1，aij=1/aji，A是隶属于z的n个因素的两两比较的判断矩阵。

(5)

先检验判断矩阵的一致性，再算出相对排序权重。其中，一致性检验的计算步骤如下。

1)计算矩阵的最大特征值λmax。

2)计算一致性指标：

(6)

3)查表，求相应的平均随机一致性指标C.I.。

4)计算一致性比率C.R.

(7)

式(7)中：C.I.是平均随机一致性指标，R.I.为随机指标。

5)判断。

当C.R.<0.1时，认为判断矩阵符合一致性；反之，当C.R.≥0.1时，认为判断矩阵A不符合一致性，需要进行修正。

相对排序权重的计算步骤如下。

（2）普通活化。将复水活化的酵母菌悬液接入乙醇含量为10%的模拟酒中继续活化30 min，记为对照（CK） 组。

1)计算判断矩阵各行元素乘积的n次方根。

(8)

式(8)中：aij是第i个指标关于第j个指标的重要度。

2)对向量M归一化。

(9)

式(9)中：Mi是判断矩阵各行元素乘积的n次方根。则W=(w1,w2,…wn)T即为所求的特征向量。

3)计算判断矩阵的最大特征根值。

(10)

式(10)中：A是隶属于z的n个因素的两两比较的判断矩阵；wi是向量M归一化的结果。

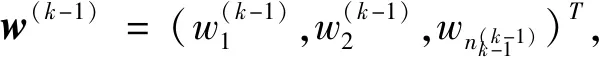
1.2.5 计算评价指标的关联函数

(11)

(12)

式(11)(12)中：K(vij)为第i级指标中第j个指标的关联函数值。

1.2.6 确定等级关联度

地铁运营火灾风险评估的物元Ni关于级别t的关联度为：

kit=∑wjKij(vij),

kit0=max{kit(Ni),t=1,2,…,s}。

(13)

2 评估体系的建立

地铁火灾风险评估体系的建立需满足系统性、科学性、可比性、可操作性和实用性原则[20-21]。

2.1 确定评价指标，构建层次结构模型

多数学者从“人、机、环、管”系统观四个维度评估地铁火灾风险，如许贵贤[12]、阳富强[14]、潘科[22]。但其观点有一定的局限性：“人”与“管”的内容有交叉，“机”和“环”的内容也有重叠。其他学者从不同的角度构建地铁火灾风险评估体系：马成正[23]从“消防设备、安全管理、应急设备、建筑与附属设施”四个方面建立了地铁运营车站的火灾风险评价指标；于恒[15]从“建筑防火、电气安全、消防设施、防火管理”四方面入手；杨阳[24]从消防设计、消防设备、环境因素、管理因素建立灰色聚类评估体系；亢磊磊[25]从防火能力、灭火能力、疏散能力、安全管理四个维度评估。

结合地铁火灾的危险性及特点，参考《城市轨道交通运营线路安全评价规范》[26]、《地铁设计防火标准》[27]、《地铁安全疏散规范》[28]以及上述学者的研究成果，从火源、防火性能、灭火能力、疏散能力、安全管理情况和环境六个方面建立地铁火灾风险评估体系，如表1所示。参考徐田坤[16]对风险水平的划分，在“较安全”“临界危险”之间增加“一般”等级，详见表2。

表1 地铁火灾风险评估体系Table 1 Fire risk assessment system for subway

续表1

表2 风险水平等级表Table 2 Risk level ranking table

3 实例分析

N市地铁已完成了两期建设规划并投入使用，线路总长约为190公里，其线网日客流量可高达248.99万人次。以N市地铁某地下二层岛式车站为例分析，该站日均上车客流约4万次。使用本文建立的评估模型，对该站火灾风险进行评估。

3.1 确定经典域和节域

以体系中的准则层一指标为例，体系中各指标的经典域及节域如表3。

表3 准则层一指标的经典域及节域Table 3 The classical domain and joint the domain of criterion layer 1 index

3.2 确定待评价物元

以二级指标中的A1人的不安全行为为例，A1的待评价物元如下：

(14)

3.3 确定各指标权重

根据1.2.4相关内容，汇总专家分值且通过一致性检验后，得出评估体系的各级指标权重。以A火源的各级指标为例，其各级指标权重见表4。

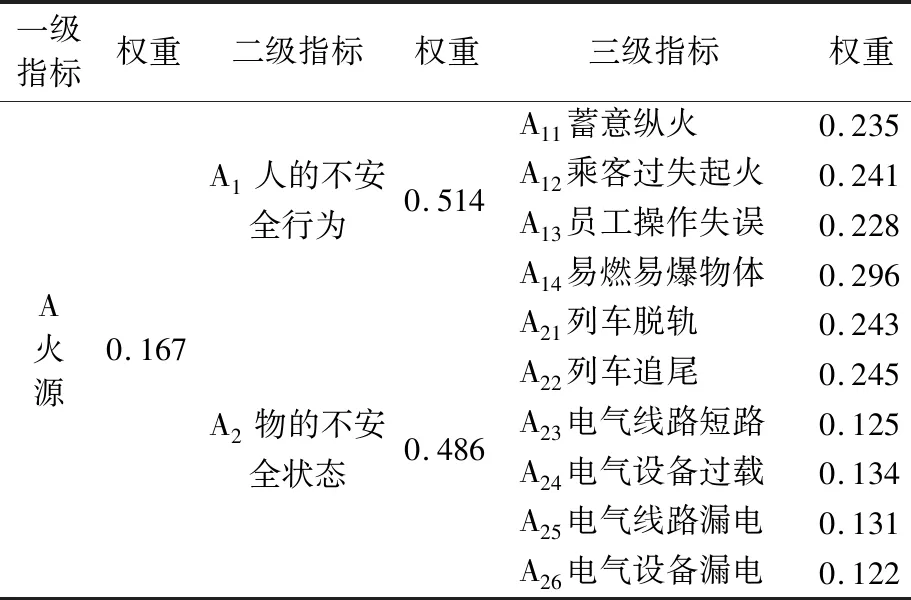
表4 体系各指标的权重Table 4 Weight of each index in the system

3.4 模糊综合评价

利用德尔菲法向专家团队发放问卷，专家团队由城市轨道交通安全领域的8名专家组成，其中副高级与正高级分别为4人。通过统计，最终确定因素层评价指标的分值后结合各指标权重计算出目标层与准则层的分值(见表5)，且得出评价的总分为91.28。通过式(11)～(13)可计算出因素层各评价指标的关联度，结果见表6(以准则层一各指标为例)。

3.5 结果分析

根据地铁火灾风险评估体系中各因素的权重可知因素在评估系统中的影响程度。在六个一级指标中，它们的权重值不相上下，其中A火源、B防火性能、C灭火能力、D疏散能力的权重值略高。A1人的不安全行为(0.514)对A火源的影响最大，A14携带易燃易爆物体(0.296)对A1人的不安全行为的影响最大。B1建筑结构(0.578)对B防火性能的影响最大，B11耐火等级(0.339)对B1建筑结构的影响最大。C1火灾自动报警系统(0.334)和C3防烟排烟系统(0.334)对C灭火能力的影响最大，C11火灾探测(0.337)和C32耐火等级(0.334)分别对C1火灾自动报警系统和C3防烟排烟系统的影响最大。D2疏散配套设施(0.335)对D疏散能力的影响最大，D21应急照明系统(0.251)对D2疏散配套设施的影响最大。

因素层的各指标等级可按照最大关联度原则确定。设风险评估水平等级为一般及以下的指标为关键因素，风险水平处于较安全等级的风险因素需加强管控，风险水平处于安全等级的风险因素应持续严格管控。分析得出：D疏散能力(包括D3疏散人员情况)和F1内部环境(包括F11鼠害情况)的风险水平处于“一般”，是关键因素，因此需要采取一系列有效的安全对策措施提升因素的安全水平；A火源、F环境的风险水平处于“较安全”，其管控还有待加强；B防火性能、C灭火能力和E安全管理情况应持续严格管控。最终算出N市某地铁站的运营火灾风险水平处于较安全的状态，虽然其风险处于可接受水平，但仍需要采取各类安全对策措施将风险最小化。

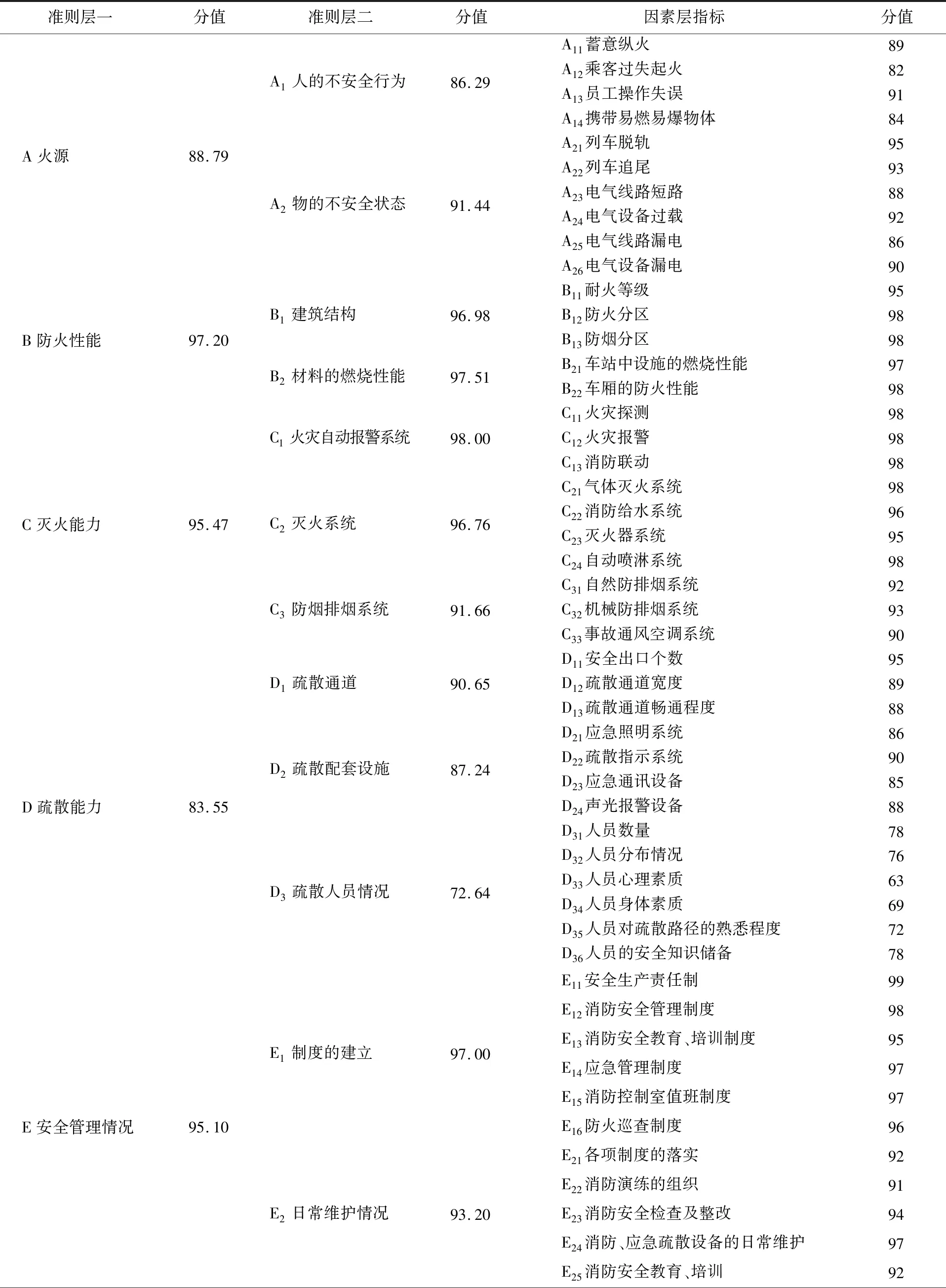
表5 体系各层指标的评价分值Table 5 Evaluation scores of indicators at each layer of the system

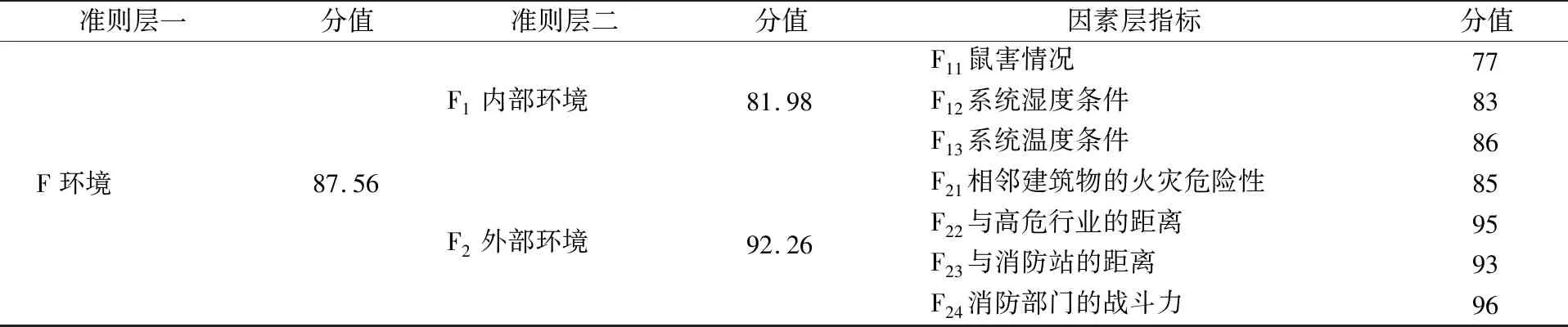
续表5

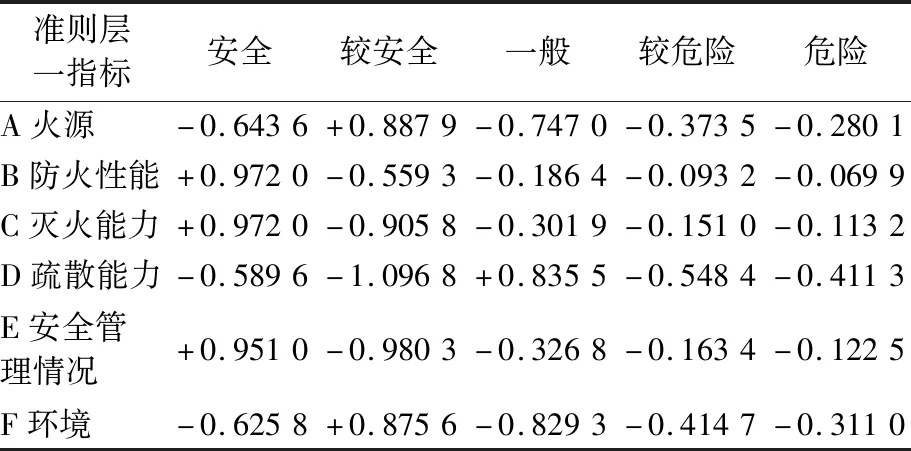
表6 准则层一各指标的等级关联度Table 6 Level correlation of each index in criterion layer 1

4 结 论

地铁被广泛应用于大中城市以缓解交通压力，由于地铁火灾事故后果较严重，对地铁运营情况下的火灾风险评估可为预防地铁火灾和应急提供科学依据。我们参考现行标准及其他学者的研究成果，建立了基于群体可拓模糊理论的评价模型，运用模糊数学、可拓理论进行综合评估，提高了评估的有效性和可靠性。将该模型应用于N市某地铁站，验证了模型的实用性，并针对火源、防火性能、灭火能力、疏散能力、安全管理情况和环境六方面的评价结果提出相应的对策措施，可为地铁运营火灾风险评估提供参考。