基于混合粒子群算法的巡检机器人路径规划

孙宗涛，朱永强

(青岛理工大学 机械与汽车工程学院，山东 青岛 266520)

近些年来，随着计算机技术在机器人领域的广泛应用，巡检机器人开始逐渐出现于人类工作的各个领域。

机器人巡检相对于人工巡检优点明显，当为其规划好一条巡视路径后，机器人就可以在无人干预的条件下按照后台指示完成相应的巡检任务，这也可以减少人工巡检的工作量。当天气环境比较恶劣或工作区设备发生故障时，它还可以降低人们受伤的风险。

由此看来，为巡检机器人找到一条合适的最短路径就尤为重要。针对巡检机器人路径规划问题，许多研究者提出了多种有效的算法，如A*算法[1]、遗传算法[2]、粒子群算法[3]、人工狼群算法[4]、蚁群算法[5]等，这些算法均取得了一定成果，同时也存在着一些缺点。

鉴于此，针对巡检机器人在工作区的路径规划问题，结合了粒子群算法的优缺点，提出了基于遗传算法改进的混和粒子群算法，通过遗传算法中的交叉和变异策略与传统粒子群算法的改进融合，采用取整交叉方法对个体与个体极值和群体极值进行交叉更新得到新粒子后，对自身进行变异从而得到更好的个体，以此种方式来搜索工作区节点之间路径的最优解。

1 建立数学模型

研究巡检机器人路径规划的目的在于，当需要机器人在工作区中进行巡检任务时，机器人根据自身当前所处位置以及工作区各个节点的位置信息，根据后台要求采用一定的路径搜索方法，快速寻找出一条耗时最短或路径最短的优化路径，并沿着此最优路径经过各个工作区节点，完成相应的巡视任务。

巡视机器人从某个起点出发，遍历工作区中各个节点的问题，此过程可看作是一个典型的旅行商(TSP)问题。旅行商问题是一个经典的组合优化问题,主要用于求解商人有且仅有一次经过N个城市并最终返回到起点的最短路径[6]。如果城市节点大规模增加的话,该问题就不可能采用穷举方式找到最优解,称为NP-Hard问题[7]。之后越来越多的学者逐步采用了启发式算法和智能算法来求解问题,以替代早期的精确算法[8]。在巡视机器人的工作场景，其巡视的TSP问题可以被定义如下：当已知工作区各节点位置横纵坐标位置时，巡视机器人从起点出发，遍历经过各个工作区节点一次，然后回到出发点，在巡视过程中找出一条距离最短的规划路径，即巡视中的优化路径满足以下方程[9]。

(1)

(2)

其中：i,j为工作区两个节点，i,j∈(1,2,…,n)；dis(i,j)为i,j两节点间欧式距离；fpath为最短遍历路径。

2 混合粒子群算法

2.1 算法理论

粒子群算法(PSO)是一种启发式随机算法。鸟群中每一只鸟相当于粒子群算法中一个粒子。粒子有三项主要特征，即速度、位置与适应度函数值，适应度函数值可以通过优化的目标函数计算而得到，之后粒子在规定的搜索空间中运动，从而寻找函数最优解。设种群中初始的粒子数目为n，当它们在规定的N维空间中进行搜索时，传统粒子群算法的更新公式如下：

(3)

(4)

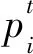
传统粒子群算法通过个体极值和群体极值来完成寻优过程，操作比较简单，收敛速度较快，但其也存在着比较明显的缺点，当迭代次数不断变大时，种群会不断收敛集中，存在于种群中的粒子相似程度也越来越高，这就导致了可能会发生陷入局部最优解的情况[10]，所以有必要对传统粒子群算法进行改进优化。

混合粒子群算法通过将遗传算法中的交叉和变异策略与传统粒子群算法的改进融合，对算法进行优化。在解决巡视机器人在工作区节点间巡视的问题中其适应度函数为遍历节点的路径长度，即：

(5)

其中：n为工作区节点数量，pathi,j为i,j两节点之间路径长度。

(1)交叉策略：采用取整交叉策略来将个体与个体极值或群体极值进行交叉更新，在获得新粒子后通过比较新旧粒子的适应度函数值来保留适应度函数值更高的粒子来完成更新过程。

(2)变异策略：首先设定变异概率来对处于粒子种群中所有的粒子进行判断是否需要变异，判定需要变异的粒子进行变异，在获得新粒子后通过比较新旧粒子的适应度函数值来保留适应度函数值更高的粒子来完成更新过程，从而得到更好的粒子。

2.2 混合粒子群算法流程

引入遗传算法中的交叉和变异策略的混合粒子群算法流程如图1所示。

图1 混合粒子群算法流程

3 试验仿真分析

为了测试混合粒子群算法的性能，使用MATLAB软件在70m×70m的巡视机器人工作区中设置了40个工作区节点。以遍历所有工作区节点为前提，路径距离最短为评价指标进行了仿真试验，每种算法在一次试验中都进行100次迭代。所设置巡视机器人二维工作区如图2所示，图中正方形块为工作区各节点。

图2 巡视机器人二维工作区模型

同时为了验证混合粒子群算法的有效性，采用传统粒子群算法、遗传算法在同样的工作区环境进行仿真试验，比较三种算法的收敛速度、最短路径距离。在上述的三种算法中，在MATLAB软件中为巡视机器人规划路径结果如图3-5所示，表1记录了在三种算法下巡视机器人具体规划路径的结果。

a 规划路径图

b 算法训练过程图图3 传统粒子群算法下的规划路径迭代图

a 规划路径图

b 算法训练过程图图4 遗传算法下的规划路径迭代图

a 规划路径图

b 算法训练过程图图5 混合粒子群算法下的规划路径迭代图

从图5中可以看出，当巡视机器人接受到巡视工作区各节点的指令时，系统在运用以上三种算法的情况下，均可为巡视机器人搜索出一条优化路径。

表1 三种算法下巡视机器人的路径规划结果

由图5和表1可知，在搜索最短路径的过程中，经过多次迭代后，传统粒子群算法经过89次迭代后，搜索出一条390.51m的最短路径；遗传算法经过78次迭代后，搜索出一条369.92m的最短路径；混合粒子群算法经过55次迭代后，搜索出一条346.58m的最短路径。从以上数据分析可知：相比于传统粒子群算法与遗传算法，混合粒子群算法在训练迭代过程中收敛更快，在全局搜索能力方面更强。

为了避免单次试验的偶然因素，使得试验结果更具可靠性，每种算法各进行了10次试验，试验结果证实了混合粒子群算法的有效性，三种算法在10次试验下每次的最短路径如图6所示。

图6 三种算法在10次试验下每次迭代的最短路径图

4 结论

针对巡检机器人的路径规划问题，提出了基于遗传算法改进的混和粒子群算法，通过遗传算法中的交叉和变异策略与传统粒子群算法的改进融合，提高了算法的收敛速度与全局搜索能力，使其发生陷入局部最优解的情况概率大大减小。通过在MATLAB软件中对三种算法的仿真试验，结果表明，相对于传统粒子群算法和遗传算法来说，混合粒子群算法具有更高的搜索最优路径的能力，具有一定的科研与实际应用价值。