冬季内燃机车燃料恒温控制系统的方案选择及仿真
郑 毅
(黑龙江工业学院 电气与信息工程学院,黑龙江 鸡西 158100)
我国北方冬季温度低,不仅会导致内燃机柴油的粘度和密度等指标造成影响,而且还会对柴油机的性能造成影响[1]。因此,针对北方冬季内燃机用柴油的恒温控制系统的研究,根据多种不同类型控制方法进行对比,选择最适合我国北方低温环境的控制方案,对柴油温度控制,不仅可以提升我国北方冬季使用柴油的性能,而且可以提升发动机的工作效率。
1 加热过程数学模型的建立
温控系统中温度过高进行自然降温处理,当温度降到最低设定值时,再次进行加热过程,循环反复。因此,只需控制加热过程。加热过程的模型建立是对油箱内的柴油温度进行研究,加热过程中的被控制量是柴油温度,则加热过程的关系式可写为[2-3]:
ΔQ=Qi-Qo
(1-1)
式中:ΔQ:系统中总的热量变化量;
Qi:系统中的输入热量;
Qo:系统中的输出热量。
加热过程的热量主要来源于高温防冻液系统的热量,辅助热量来源于其他元器件工作中生成的热量,辅助热量可以忽略不计[4],则在Δt时间内,加热过程的关系式可整理为:
cρVΔT=Q(t)Δt-K'A(T(t)-Ts)Δt
(1-2)


(1-3)
经计算验证可得Q(t)的数值要远远大于K'ATs的数值,所以K'ATs可以近似舍去[5],加热过程中的响应也必定会有惯性和滞后的特性,进行拉氏变换整理后可得:
(1-4)
式中:C—柴油的比热容(KJ/(kg·℃))
ρ—柴油的密度(kg/L)
V—恒温油箱容积(L)
K'—油箱散热系数(w/(m2·℃))
A—油箱散热面积(m2)
2 加热过程参数选定
根据相关规定对传递函数式子中的相关参数进行选定,具体如下:
铁路运输系统中对机车使用的规范明确规定,加载运行时的油水温度必须要高于40℃时才可以。《柴油温度对柴油机性能的影响》中提及,柴油温度在40℃时的柴油密度为0.8955kg/L。
柴油的比热容C根据《国标柴油和汽油质量指标》查询为2.1KJ/(kg·℃)。
经测量防冻液的进口温度Ti为89℃、防冻液的出口温度TO为86℃。
根据TB/T3208-2008《散装颗粒货物运输用防冻液技术条件》[6]中提到内燃机车专用防冻液密度ρ0为1.100g/cm3~1.600g/cm3;防冻液的比热容C0为4.05KJ/(kg·℃)[6]。
实验选择长宽高比例为1:1:2的油箱,体积V选择容量为40L[7]。
经过文献的查询,对于油箱的散热面积计算公式近似为[7-8]:
(2-1)
式中H—油箱总的发热量(kcal/h);
K'—油箱散热系数(w/m2·h·℃);
T1—油箱内柴油温度(℃);
T2—油箱外部环境温度(℃);
A—油箱散热面积(m2)。
在油箱的长宽高比为1:1:2或1:2:3,以及油液深度是油箱高度的0.8倍时,则有油箱散热面积A与油箱容积V有如下的关系式[9]:
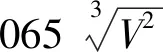
(2-2)
式中V—油箱的有效容积(L);
A—油箱散热面积(m2)。
将本文油箱的实际容积带入2-2式中,可求得油箱散热面积A为0.76m2。
油箱散热系数K'依照文献《基于三级油箱结构的精密油温控制系统》中提到,油箱散热系数K'为0.03w/(m2·℃)[10]。
仿真时间t和滞后时间τ分别设定为150s和2s。
柴油的初始温度T0根据文献《寒冷冬季内燃机车的预热问题》中有提及,内燃机车出库前加热打温范围为20℃~40℃。
JB3743—1984《汽车发动机性能试验方法》第5、6款已经对调节柴油的温度定制了规范,温差区间规范在37℃~43℃比较适合[11]。当柴油温度升高时,柴油的消耗量降低,柴油成本降低,但柴油的运动粘度降低,导致柴油的燃烧效率降低。所以温度越高,柴油的燃烧效率越低。因此,综合考虑各方面因素,本文确定柴油的目标温度定为43℃。
整理后可得加热过程仿真中用到的实际指标参数如表1所示。
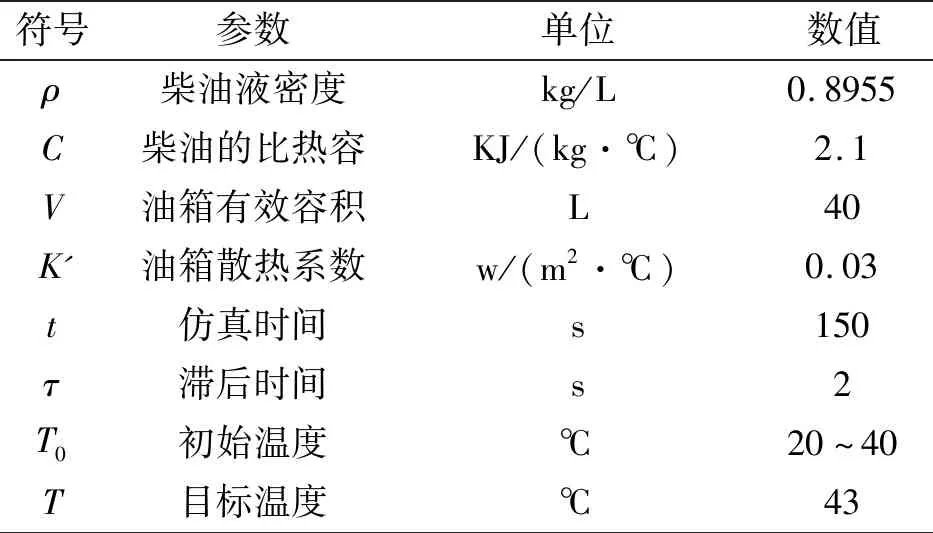
表1 加热过程仿真参数
将表1所涉及到的加热过程参数通过单位换算后带入(1-4)式中,得到加热过程传递函数:
(2-3)
3 PID参数整定
PID控制中选择适合系数,会使系统运行平稳,否则可能出现震荡超调。根据本系统要达到的性能指标和控制效果,经过研究发现数字型增量式PID控制最为适合。PID参数整定主要在时域内研究和频域内研究。本文温度随时间变化,符合时域规律,因此选择时域PID控制器整定。
时域内常用的整定方法有Z-N法、CHR法、C-C法、IMC法和OPT法。不同的时域内对系统的PID参数进行整定的常用方法规则[12]如表2所示。

表2 时域内系统的不同的PID参数进行整定法的整定规则
将(1-4)式子经整合得到加热过程的化简后的传递函数为:
(3-1)
式中,K—被控对象的开环增益;
T—惯性时间常数;
τ—纯滞后时间常数。
本文设定采样周期T'=1s,比较选择被控对象的开环增益K=44,惯性时间常数T=3299,纯滞后时间常数τ=2。根据表2时域内系统的不同的PID参数进行整定法的整定规律,可得到不同整定法的三个系数指标[13]。
Z-N法求得
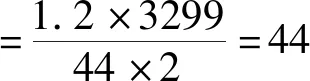

CHR法求得
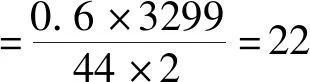

C-C法求得
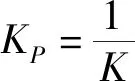

IMC法求得

KI=KPT'/TI=0.0000069;KD=KPTD/T'=0.023。
OPT法求得

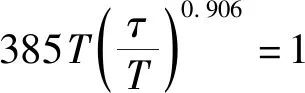
根据时域内系统的不同的PID参数进行整定法的整定规律原则,通过对不同整定法计算得到的三个系数指标整理后如表3所示。
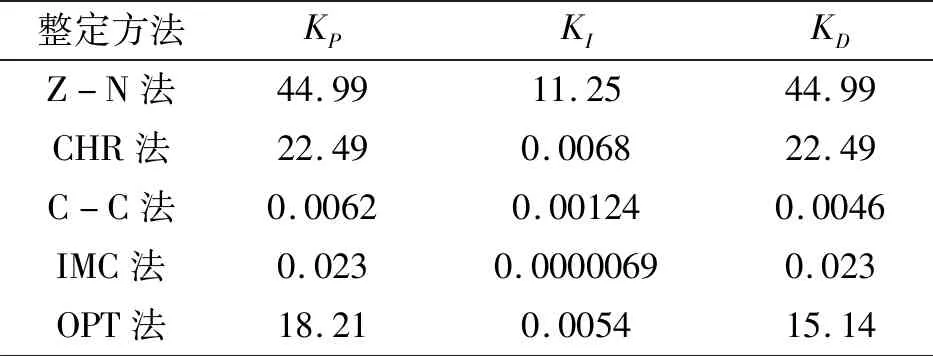
表3 时域内系统的不同的PID参数
4 加热过程数学模型的仿真

图1 不同PID整定法加热过程仿真界面
从图1中可知,将五种整定方法的仿真结构各自集合在模块中,而五个模块内部仿真结构相同,其中以Z-N法模块为例,其内部仿真结构如图2所示。

图2 五种整定方法内部仿真结构
当给定值为43时,时域内系统的五种参数整定法在加温过程仿真结果的温度图形的对比曲线如图3所示。
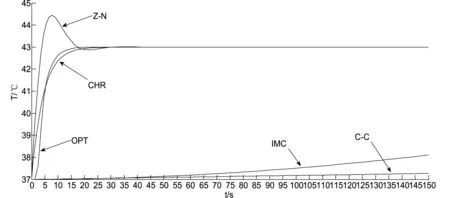
图3 五种不同时域整定法加温过程温度仿真比对结果
从图3中可看出,虽然在用CHR法和OPT法进行运算的规则和最终得出的参数均不相同,但是从结果中可以看出却极度相近,温度上升平稳,虽然没有超调,但是上升速度并不算快;从C-C法和IMC法得到的结果不难看出,两种方法的积分系数KI数值过小,导致在短时间内温度升不上去,不能达到设计的指标和要求。使用Z-N整定法对参数进行整定时,数值快速上升,但是在到达设定值43时并未停止,此时进入超调过程,但是在极短的时间内进行了抑制,并最终稳定保持在设定值43,超调幅度小,反应时间短,抑制能力强。
综上所述,根据加热过程模型可知,本系统的惯性时间常数远大于滞后时间常数,针对这类传递函数和模型来讲,一般情况下应用Z-N整定法整定最为适合,整定结果也是最优的。经过对比,虽然Z-N法在温度上升的过程中有少许超调,但是在温度上升的过程中有自身抑制超调的效果,最终达到要求指标,加温速度最快,加温过程也是最稳定的,超调幅度小,反应时间短,抑制能力强,非常适合本设计所应用的环境,选用Z-N整定法对PID进行整定。
结语
本设计依据热平衡定律对我国北方冬季铁路运输中的柴油加热过程进行了数学模型的建立,根据实际参数推导出传递函数,并对参数和控制方案进行了选定,通过已有常用的PID整定方法进行比对,选取最为适合本设计的整定方案,并进行参数整定及对加热过程进行仿真。最终选择最为合适的整定方法,取得了令人满意的效果。

