具波动算子非线性Schrödinger方程线性化差分格式

闫瑞娥，梁宗旗

(集美大学理学院，福建 厦门 361021)

0 引言

非线性Schrödinger方程是一类经典的非线性偏微分方程，在量子力学、非线性光学、流体力学等中均有广泛应用。具波动算子的非线性Schrödinger方程是Matsunchi[1]于1980年在研究单色波的非线性相互作用时首次得到的。随后在推导高频电子横向速度、研究等离子物理孤立子等问题的许多物理模型所满足的方程中也得到了同类方程。具波动算子的非线性Schrödinger方程与经典的非线性Schrödinger方程相比，在非线性Schrödinger方程基础上增加了波动项和一阶项，使其同时具有波动方程与抛物方程的性质，从而使该问题的研究变得更加复杂且具有挑战性。关于该方程的研究文献不多，郭柏灵[2]研究了该方程多维问题的初、边值问题，证明了其解的存在性与唯一性，并研究了其正则性；文献[3]研究了特殊情况下该类方程一维情况下的数值解问题；文献[4-6]构造了该方程的显式差分格式、谱方法及拟谱方法，并分别证明了其稳定性；文献[7-9]在文献[3]的基础上给出了一类特殊情况下该方程的多种守恒差分格式；文献[10]给出了该方程的一种高精度守恒差分格式；文献[11]给出了有限元方法；文献[12]和文献[13]分别给出了该方程的 一类多辛傅里叶拟谱格式和指数波积分的傅里叶谱方法；文献[14-15]构造了多种该类方程的多辛格式；文献[16]研究了特殊情况下该类方程的行波解的线性稳定性问题；文献[17]和文献[18]分别给出了规范变换后的多种组合解、Jacobi椭圆函数周期解及新的多级包络周期解，并在极限情况下求得了该方程的多类精确孤波解；文献[19]和文献[20]分别给出了该类方程的多尺度时间积分与两尺度方法、能量守恒的哈密尔顿边值方法；文献[21-24]分别给出了守恒差分格式、守恒紧格式及Galerkin谱方法等。

本文研究如下形式的具波动算子的非线性Schrödinger方程

(1)

其中:i2=1;Tu=utt-uxx+γutx;ut=∂u/∂t，ux=∂u/∂x，utt=∂2u/∂t2，uxx=∂2u/∂x2;utx=∂2u/(∂t∂x);α，γ，δ2，β>0为实常数；u(x，t)是未知复值函数；u0(x)，u1(x)均为实值函数;L=xr-xl。

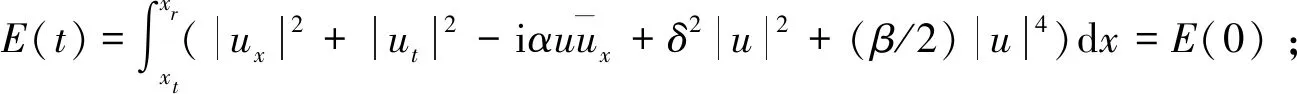
在数值计算中，为了拟合原方程具有的守恒性，构造的格式也能保持原方程的守恒性，称之为守恒格式。但守恒格式在一般情况下都要求解一个非线性方程组，加入一个小参数，这给实际计算带来了很多的问题和困难。例如，如果选择合适的迭代法、收敛速度等，如构造的格式是显示格式，一方面是显示格式是否稳定，即使是稳定，一般其稳定性条件都是比较苛刻的。因此，本文提出了对非线性项在时间层利用Taylor展开，将非线性格式转化为线性化差分格式的差分方法。

1 线性化格式构造

先构造如下的守恒“蛙跳”差分格式:

(2)

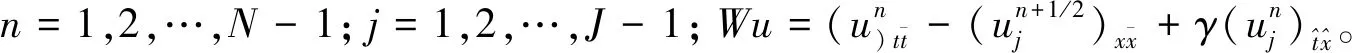
显然上述的格式为全隐格式，需要求解一阶非线性方程组或采用预估一校正方法求解。为了避免求解非线性方程组,引入一个小参数对非线性项进行处理。

(3)

其中R(τ)=o(τ2)是截断误差。对式(3)引入小参数(∈R)，舍去误差项后得

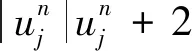
(4)

(5)

将式(5)代入式(4)并整理得

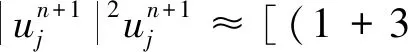
(6)

将式(6)代入差分格式(2)中非线性项，非线性项部分变为如下形式:

(7)

(8)

令s=τ/h,式(8)可以改写成:

(9)

其中:1≤j≤N-1;n=1，2，…;D=4+4s2+2iατ+2τ2δ2;E=iατs+γs-2s2;F=-iατs-γs-2s2;Mj=8-2βτ2[(1+3)令Un=(u1，u2，…，uN)T。

根据式(9)对应的所有网格点及方程(1)给出的初、边值条件，得到如下形式的线性代数系统：

LUn+1=MUn+PUn-1,

(10)

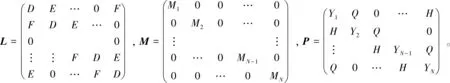
2 稳定性分析

(11)

(12)

其中：A=-4s2cos(ξh)-2sατsin(ξh)+4+4s2+2τ2δ2；B=2sγsin(ξh)+2ατ。

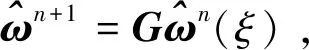
设增长矩阵G的特征方程为λ2-bλ+c=0,其中b=[8-2βτ2(1+)C2]/(A+Bi)，c=-[2βτ2(-1)C2-A+Bi]/(A+Bi)。

根据Fourier稳定性分析方法，要保证格式稳定，需要满足|λ|≤1，即|b|≤2，|c|≤1。为满足上述条件,只需满足以下条件即可

|[8-2βτ2(1+)C2]/(A+Bi)|≤2,

(13)

即

[4-βτ2(1+)C2]2-B2≤A2。

(14)

式(14)是关于h的四次不等式，得到h与τ的关系是一个简单而运算复杂的过程。为方便起见，考虑一种特殊情况:

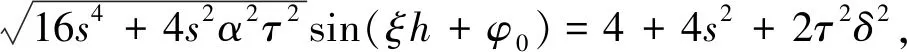
(15)

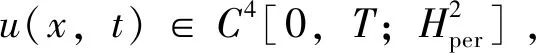
类似于稳定性定理1的证明,可类似得到如下的收敛性定理2。

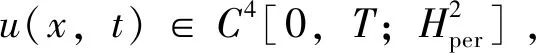
3 数值实验

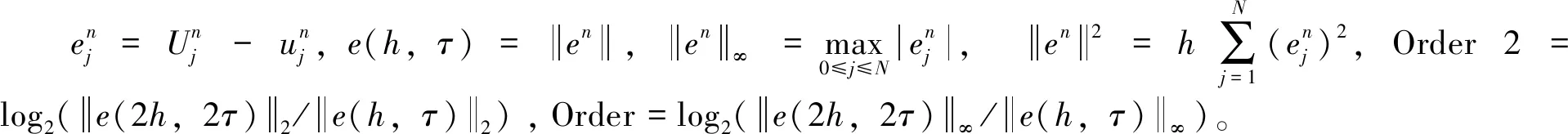
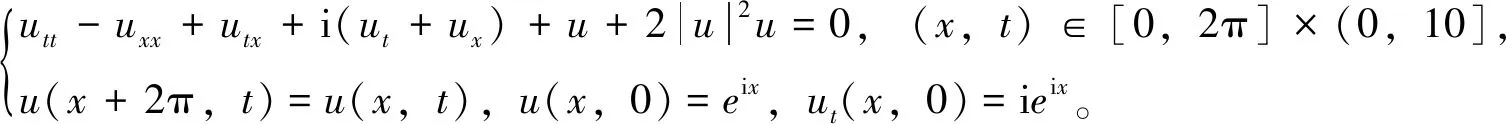
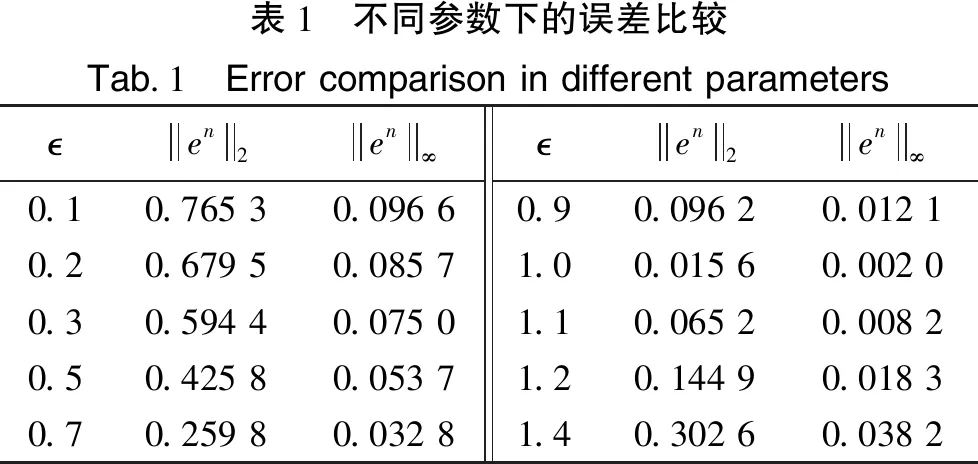
表1 不同参数下的误差比较Tab.1 Error comparison in different parametersen2en∞en2en∞0.10.765 30.096 60.90.096 20.012 10.20.679 50.085 71.00.015 60.002 00.30.594 40.075 01.10.065 20.008 20.50.425 80.053 71.20.144 90.018 30.70.259 80.032 81.40.302 60.038 2

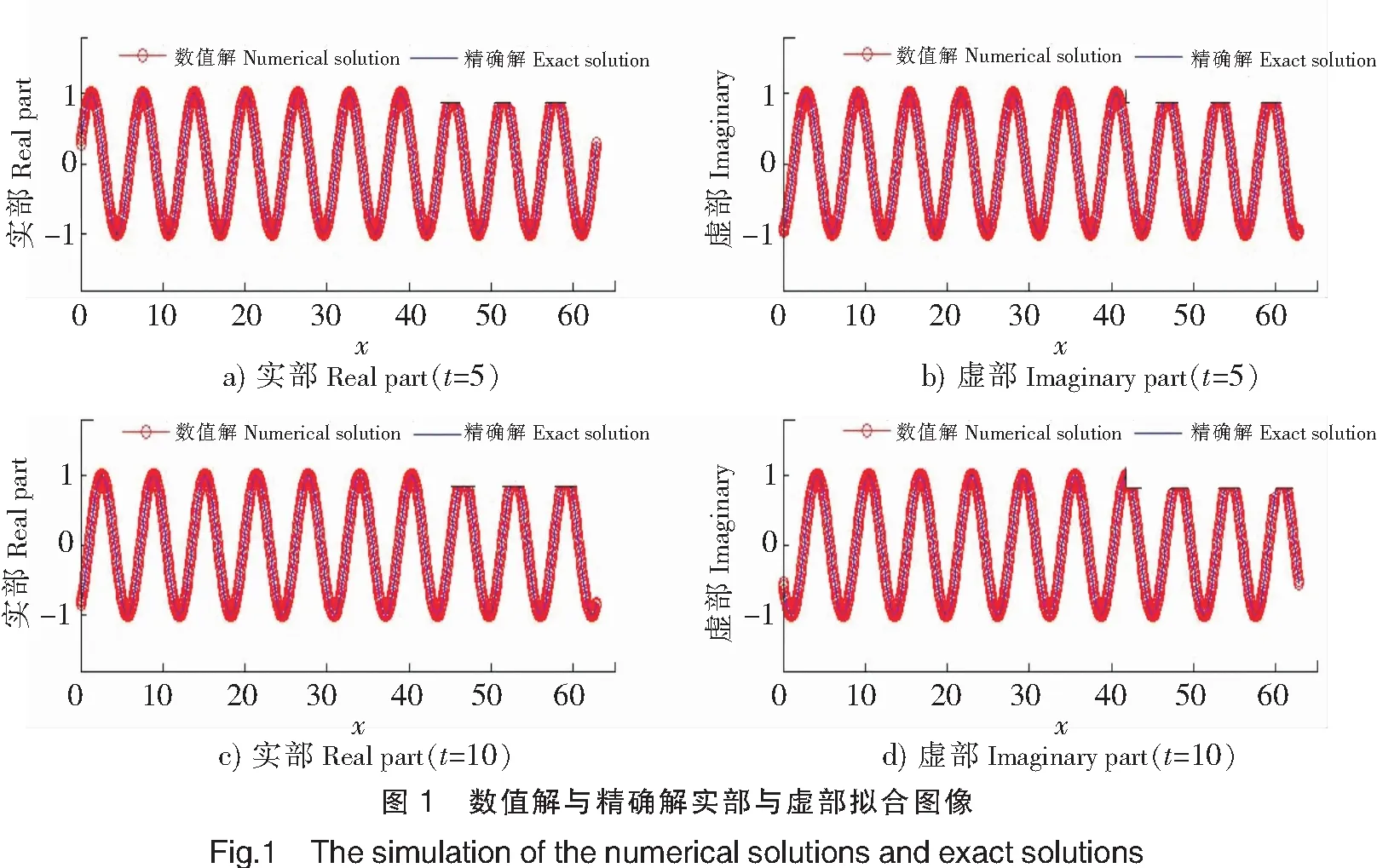
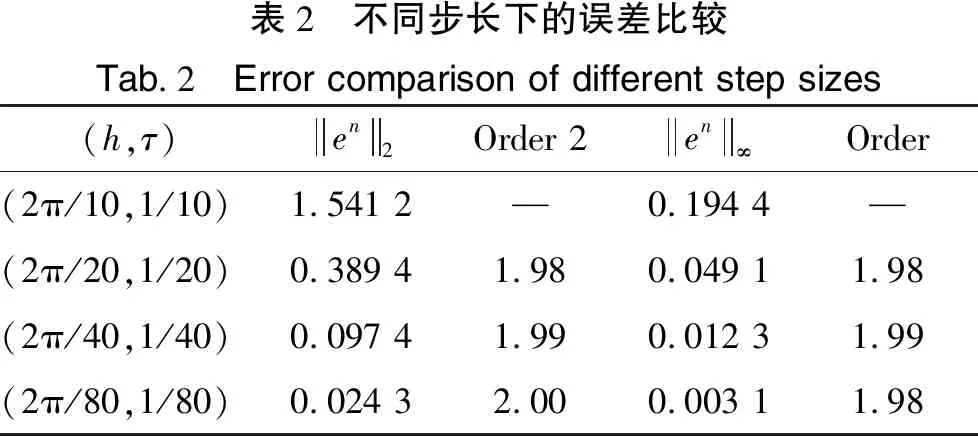
表2 不同步长下的误差比较Tab.2 Error comparison of different step sizes(h,τ)en2Order 2en∞Order(2π/10,1/10)1.541 2—0.194 4—(2π/20,1/20)0.389 41.980.049 11.98(2π/40,1/40)0.097 41.990.012 31.99(2π/80,1/80)0.024 32.000.003 11.98

与文献[21-24]相比，本文提供的格式是线性化格式，在相同精度要求下只需求解一个线性方程组，可以用显示的追赶迭代法求解，大大节省了运算时间，求解的复杂度明显降低，说明本文提出的格式是一种高效的、简单的稳定格式。

4 结论

本文在“蛙跳”格式的基础上，通过对非线性部分进行处理，将原来的全隐格式转化为线性化格式，得到了一个带小参数的修正的线性化格式，并证明了其收敛性与稳定性。通过数值算例，验证了该结果的可信性和有效性。此格式最大的优势是将原全隐格式需求解一个非线性方程组的问题转化为只需求解一个线性方程组，大大简化了运算，提高了计算效率。此外，新方案与文献[11]中的方案进行比较，无论是在计算时间还是模误差，本文构造的带小参数的线性化格式远远优于文献[11]，计算效率明显提高，是一种简单易行、有效快捷的数值方法。