一种高效的范围证明方案*

张 凡,高 胜,2,曾志强,刘 喆

1.兴唐通信科技有限公司,北京100191

2.数据通信科学技术研究所,北京100191

3.信息保障技术重点实验室,北京100072

4.北京理工大学信息和电子学院,北京100081

1 引言

2008年,化名Satoshi Nakamoto(中本聪)的学者在网络上发表了一篇题为《比特币:一种点对点的电子现金系统》的文章,于是比特币[1]进入人们的视野.历经十余年的发展,各种数字货币纷纷出现,例如门罗币[2,3]、零币[4]、莱特币[5]等.比特币具有去中心化,分布式记账以及用户身份匿名等优点.然而值得诟病的是,交易金额是明文传输的,这严重限制了比特币的广泛应用.随后诸如门罗币和零币等数字货币采用各种密码技术(比如环签名[6]等特殊数字签名、承诺[7]、零知识证明[8]、同态加密等)来解决交易金额的隐私保护问题.例如门罗币采用Borromean环签名结合 Perdersen承诺[9]来实现对交易金额的隐藏,零币则采用zk-SNARK[10–12]这类零知识证明对交易身份以及交易金额进行隐藏.

区块链作为数字货币的支撑技术,本质上是采用链式数据结构来验证和存储数据并结合分布式共识机制来生成并更新数据,从而保证全网诚实节点的状态一致性.去中心化、可验证以及防篡改是区块链技术的基本属性.随着对区块链技术的深入研究以及其可能的应用场景的探讨,敏感数据的隐私保护问题显得尤为重要.在区块链系统[13]中,隐私保护主要体现在两个方面:匿名性和秘密性.其中匿名性是指交易发起者和交易接收者的身份隐藏,而秘密性是指交易金额的隐藏.目前比特币系统只提供弱匿名性,即交易发起者和交易接收者的真实身份与其对应的公钥没有关系.门罗币和零币虽然能解决隐私保护问题,但门罗币中证据的长度较大,而零币需要可信任第三方的参与并且证据生成时间很长.因而给出一个高效简洁的隐私保护方案是一个非常有挑战的问题.

为了保障交易的秘密性,Maxwell等人提出秘密交易 (CT)[14]概念,即交易发起者对交易金额做承诺,然后给出相应的证据证明该金额在某个公开的范围内.Maxwell等人利用Borromean环签名给出一个具体的范围证明方案,该方案无需可信第三方的参与,然而证据长度比较庞大并且证据生成和证据验证的时间复杂度也不小(均与金额的比特数线性相关),因此该方案在实际应用中很受限.Jan Camenisch等人于 2008年提出基于 Boneh-Boyen签名[15]的交互式范围证明方案[16],该方案后来被 Shunli Ma等人[17]借鉴用来保护交易金额的隐私性,由于该方案利用双线性对并且需要可信第三方的参与,虽然证据长度很短,但验证时间比较长.2017年,Benedikt Bunz等人[18]提出新的范围证明方案,该方案借鉴Jonathan Bootle[19]等人提出的基于多项式承诺的零知识证明方案,并利用向量内积承诺方案将证据长度减为对数级别.该方案不仅不需要可信第三方的参与,而且将证据长度大大降低并且减少证据验证的时间复杂度,这使得该方案能很好地应用在区块链系统中.本文在 Benedikt Bunz等人工作的基础上提出了一个新的范围证明方案,该方案将金额按两比特划分并构造新的可满足性电路,然后借鉴 Jonathan Bootle等人的零知识证明方案和向量内积承诺,将证据的生成时间和证据的验证时间大幅减少.结合Jonathan Bootle等人的零知识证明方案以及向量内积承诺的安全性证明,很容易给出本文提出的范围证明方案的安全性证明.当公开区间为[0,264)时,本文方案不仅将证据生成时间减少近一半,而且将证据验证时间减少约 33%.为了对这些范围证明方案有一个直观的认识,表1给出这四个方案的性能比较,其中ct表示椭圆曲线中标量点乘的时间复杂度,cs表示椭圆曲线中点的长度.容易看出本文的范围证明方案更适合应用在区块链系统中来保护交易金额的隐私.

本文的结构如下:首先第2节介绍符号定义、Pedersen承诺以及多项式承诺的基本概念.接下来第3节介绍Jonathan Bootle等人提出的对任意函数的零知识证明方案.第4节给出本文的范围证明方案.最后第5节对本文做出一个总结.

表1 n=64,m=8具体方案性能比较Table 1 Performance comparison among specific schemes with n=64,m=8

2 预备知识

本节首先介绍一些符号定义,然后介绍Pedersen承诺、多项式承诺以及向量内积承诺等基础知识.

2.1 符号定义

下面介绍本文将要使用的符号定义.

G 满足离散对数困难问题的乘法交换群

g群G的生成元

q群G的阶,为大素数

Zq模q的整数环

H抵抗碰撞的哈希函数

◦向量的Hadmard积

·向量的内积

⊕异或运算

ct G上随机元素指数运算的计算复杂度

ce G上双线性对运算的计算复杂度

cs G上元素的长度

本文规定加粗的字符表示向量,未加粗的字符表示集合中的元素.并且规定这里g=(g1,g2,···,gn)∈Gn,a=(a1,a2,···,an)∈. 规定两个向量多项式a(X),b(X)∈[X]的乘积运算c(X)=a(X)·b(X)为多项式乘法并且系数之间的乘法定义为内积,此时c(X)∈Zq[X].

2.2 Pedersen承诺

Pedersen承诺[9]是由双方参与的协议.定义公开参数ck={G,q,g,h},这里g是G的生成元,h∈G且其离散对数未知.

定义 1(Pedersen承诺)Comck(a;r):=grha为对a的Pedersen承诺,这里r是随机数且不公开.

而多元 Pedersen承诺类似于 Pedersen承诺,即给定公开的参数 ck=(G,q,g,h1,···,hn),这里g是 G 的生成元,(h1,···,hn)∈Gn,这些点的离散对数均未知.给定消息 (m1,···,mn)∈,则对应的Pedersen承诺为

Pedersen承诺满足隐藏性(Hiding)和绑定性(Binding):

隐藏性:承诺值和随机数在计算上不可区分.由于r是随机数,C0=grha0和C1=grha1在计算上是不可区分的,进而隐藏承诺内容.

绑定性:在承诺做出之后,承诺内容不可抵赖.假设存在r′和a′̸=a使得grha=C=gr′ha′,则有h=g(r−r′)(a′−a)−1,这说明h的离散对数已经被求出,而这与离散对数的困难性假设矛盾,因此绑定性满足.

2.3 多项式承诺

假设证明者拥有多项式t(X)=t0+t1X+t2X2+···+td−1Xd−1,则该多项式承诺是一个三段式协议,具体流程如下:

(1)证明者计算pc←PolyCommit(t(X)),即对t(X)的每个系数做承诺,

这里ck={G,q,g,h},然后将pc发送给验证者.

(2)验证者随机选择x∈,并将其发送给证明者.

(3)证明者计算 pe←PolyEval(x,t(X)),这里 pe=(v,ρ),其中v=t(x),ρ=;并将 pe发送给验证者.

(4)验证者计算v←PolyVerify(pc,pe,x),这里

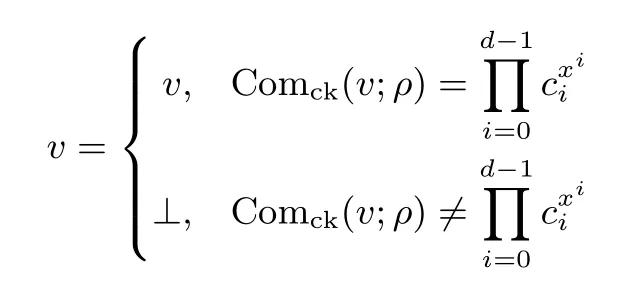
利用Fiat-Shamir方法,该承诺方案变为非交互式承诺方案,此时x=H(pe,ck).于是证明者公开承诺值(pe,v,ρ),验证者则计算x并调用PolyVerify(pc,pe,x)验证该承诺是否合法.

注意到承诺的长度会随多项式的次数d增加而线性增加.为了降低承诺的长度,文献 [19]将多项式的系数分段并构造矩阵,然后对矩阵的每一行做多元 Pedersen承诺并构造新的多项式承诺方案,此时承诺长度为

2.4 向量内积承诺

向量内积承诺是指证明者拥有两个秘密向量a,b∈,公开c=a·b以及A=ga和B=hb,证明者向验证者证明A和B所蕴含的向量a和b之内积确实为c.

下面介绍文献[19]提出的向量内积承诺方案,不妨将该方案记做(G,g,h,A,B,c,n;a,b),这里g和h中每个元素的离散对数互不知晓且n为二的幂次方.

首先将n维向量切成2个块,每个块是n/2维的向量,记

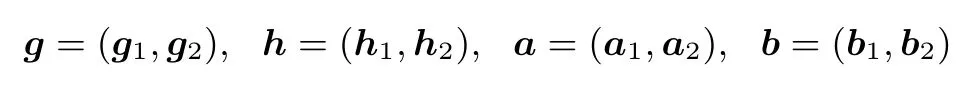
这里g1,g2,h1,h2∈Gn/2,a1,a2,b1,b2∈,则

如果令A′=(g′)a′,B′=(h′)b′,则原向量内积承诺转化为对新向量a′和b′的内积承诺.注意到验证者需要计算g′,h′,A′,B′以及c′,证明者需要传输Ak,Bk和ck,这里k∈{−1,1}.

下面描述该向量内积承诺方案(G,g,h,A,B,c,n;a,b)的具体过程,这里只有a和b是秘密.在下面的过程描述中,P是指证明者,而V是指验证者.

公开输入:g,h∈Gn,A,B∈G,c∈,并且假设n为二的幂次方.

秘密输入:证明者拥有(a,b)且满足A=ga,B=hb以及c=a·b.

协议过程:(1)当(n>1)时,执行递归约减步骤:

•P→V:发送A−1,B−1,c−1,A1,B1,c1共 6个元素 (注意到A0=A,B0=B和c0=c,这三元组不用发送);

•P←V:发送随机数x∈;

•P→V:P和V分别将原始知识证明问题转化为如下知识证明问题

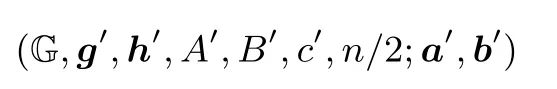
这里

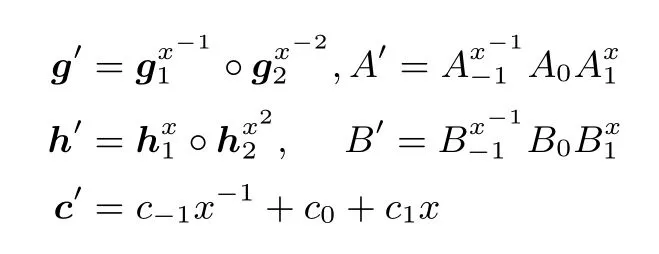
此外,P还需更新自己的秘密输入,即a′=a1x+a2x2和b′=b1x−1+b2x−2.

然后P和V循环执行该递归约减步骤.

(2)当(n=1)时,执行终止步骤:

•P→V:P直接发送(a,b);

•P←V:如果A=ga,B=hb以及c=ab成立,则返回接受,否则拒绝.

上述方案中证明者需要向验证者发送Ai,Bi以及ci,所需的通信带宽较大.为了降低通信复杂度,文献[18]考虑P=gahb,这里c=a·b,gt的离散对数未知.此时在递归约减的步骤中Ai,Bi和ci可以合并发送.不妨将该承诺方案记做(G,gt,g,h,P,n;a,b),下面是其具体过程.

公开输入:g,h∈Gn,gt,P∈G,这里n是二的幂次方.

秘密输入:证明者拥有a=(a1,a2),b=(b1,b2)并满足,这里

g=(g1,g2),h=(h1,h2),c=a1·b1+a2·b2

协议过程:如果n=1,则

•P→V:直接发送(a,b)

•P←V:如果P=gahb,这里c=ab,则返回接受;否则拒绝.

递归约减:如果n>1,则证明者令n′=n/2,然后计算

•P→V:发送 (L,R),这里cR=a2·b1∈Zq.

•P←V:发送随机数x∈

•证明者和验证者将原问题转化为如下新问题

(G,gt,g′,h′,P′,n′;a′,b′)

这里

而且证明者还需计算

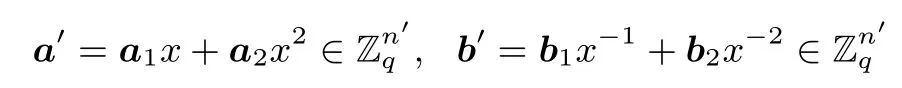
综上,第一个向量内积承诺方案的通信复杂度为6logn+2,而第二个向量内积承诺方案的通信复杂度为2logn+2,而且第二个方案的计算复杂度比第一个方案小.引理1给出这两个内积承诺方案的安全性.

引理 1上述向量内积承诺方案具有完美完全性 (perfect completeness)和统计的见证扩展仿真性(statistical witness-extended-emulation),即提取出非平凡的离散对数或者提出有效的见证(witness).

证明请参考文献[18].

3 算术电路的无中心零知识证明方案

零知识证明由 Goldwasser等人[21]于上世纪 80年代提出.它是一种密码学技术,通过交互,证明者向验证者证明某个提议是正确的并且无需泄露除了它是正确之外的任何信息.后来,Goldreich等人[22]证明任何 NP问题都有零知识证明系统.至此人们提出许多零知识证明方案,其中最为著名的是 Fiat-Shamir零知识身份认证协议[23–25],其安全性建立在大整数分解问题的困难性,然而其通信和计算复杂度太大,因而实用性不强.2013年,Parno等人提出匹诺曹协议[10],该协议是一个简洁非交互式零知识证明协议(zk-SNARK),并且用于对任意布尔 (或算术)电路的可信计算.该协议最大的优势是无论可满足性电路有多复杂,其证据的长度固定为 288字节.2016年,Bootle等人[19]提出另外一种零知识证明协议,该协议同样用于对任意布尔电路的可信计算.与匹诺曹协议不同的是,该协议不仅无需可信第三方以及复杂的预计算过程,而且其安全性只依赖于离散对数的困难性.2017年,Bootle等人[26]提出可以批处理的零知识证明,该方法将多个秘密满足的简单电路转化为低次数的多项式,进而利用多项式承诺给出高效的证明.2018年,Wahby等人[27]提出新的zk-SNARK协议Hyrax,该协议结合Pedersen承诺、求和验证协议等密码学工具对任意电路实现可信计算,并且无需可信第三方以及安全性假设只依赖于离散对数问题.除此之外,Huige WANG等人[28,29]借鉴这类对可满足性电路的零知识证明方法并应用在功能加密和访问控制加密中.

本节介绍Bootle等人的零知识证明方案,其中3.1节介绍算术电路转化为代数表达式的过程,第3.2介绍代数表达式转化为向量多项式的过程,接下来3.3节介绍基于多项式承诺的零知识证明方案,最后3.4节给出该零知识证明方案的具体过程.

3.1 算术电路的代数表达式刻画

本节介绍将任意给定算术电路转化为代数表达式的过程.

如图1所示,首先对每个乘法门分配相应的(ai,bi,ci),其对应的代数表达式为aibi=ci;其次对于常数乘法门以及异或门,利用相关输入输出的仿射表达式刻画,例如图1中右侧的线性表达式给出了常数乘法门和异或门的代数刻画.

图1 算术电路的代数表达式刻画Figure 1 Algebraic expression of arithmetic circuity

假设该电路图的乘法门个数N=m∗n,(ai,bi,ci)则用三个m∗n的矩阵 (A,B,C)表示,定义A◦B=C,这里A,B和C的每一行表示为

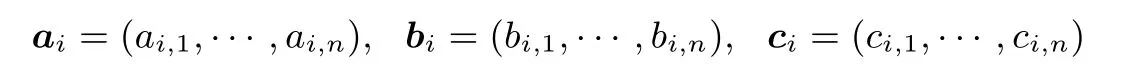
且满足ai◦bi=ci,其中i∈{1,···,m}.每个仿射表达式的刻画表示如下

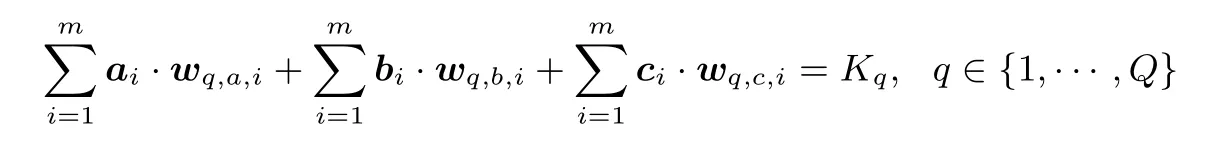
这里wq,a,i,wq,b,i,wq,c,i和Kq是只与电路有关的常数,Q是仿射表达式的个数.

3.2 算术电路的多项式转化

本节介绍将代数表达式转化为单变元多项式的过程.设Y是自变量,定义Y′=(Ym,Y2m,···,Ynm)和Y=(Y,Y2,···,Ym),则Y(A◦B)Y′T=YCY′T,展开得

即Yi+jm对应的系数满足ai,jbi,j=ci,j.令M=N+m,对于Q个仿射表达式,则有

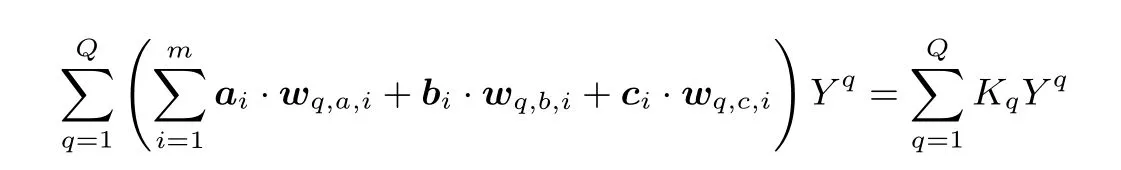
将上面的两个表达式联立,有

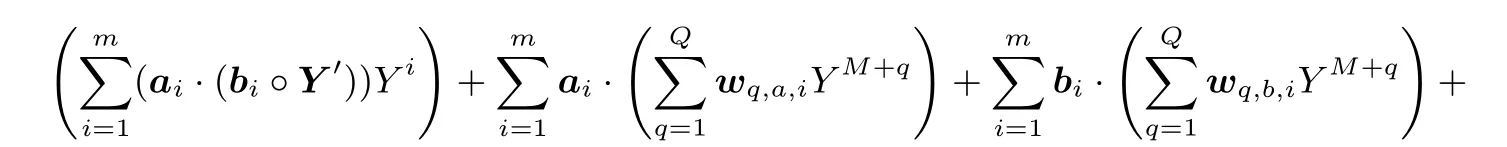
定义

于是电路是可满足的当且仅当

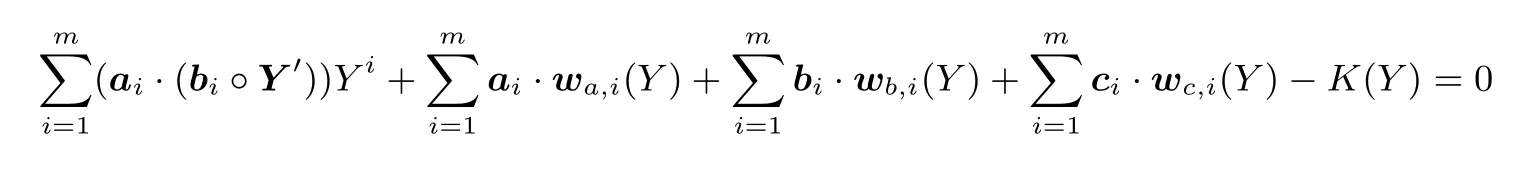
设验证者发送随机数y∈,此时证明者需要证明

这里y′=(ym,y2m,···,ynm).

3.3 基于多项式承诺的零知识证明

根据算术电路的代数表达式刻画,证明者构造如下洛朗多项式:

这里d为盲化向量.容易验证t(X)的常数项为零.

一种非常直接的思路是,证明者首先将ai,bi,ci和d的承诺发送给验证者,随后验证者随机选取y∈并将其发送给证明者,接下来证明者利用PolyCommit将t(X)的承诺pc发送给验证者,验证者随后随机选取x∈并将其发送给证明者,然后证明者将r(x)以及由PolyEval产生的pe一并发送给验证者,此时验证者首先根据ai,bi,ci和d的承诺验证r(x)的正确性,然后计算s(x)和K(y)以及r′(x),接着验证者根据(pc,pe)验证承诺的正确性并计算t(X)在x处的取值,最后验证者判断t(x)r(x)·r′(x)−2K(y)是否成立即确定该证据是否为对应电路的合法零知识证明.

文献[18]的作者利用向量内积承诺给出更高效的证明方案.注意到

这里Ai,Bi,Ci和D分别是ai,bi,ci和d的承诺,即

Ai=Comck(ai,αi),Bi=Comck(bi,βi),Ci=Comck(ci,γi),D=Comck(d,δ)

其中 ck={G,q,g,g=(g1,g2,···,gn)}. 如果令,则gr=hr◦y′并且hr′=grh2s.设v=t(x),则r·r′=v+2K(y).此时该零知识证明方案转化为如下向量内积承诺方案

(G,g,h,R,R′,v+2K(y),n;r,r′)

这里R=gr,R′=R∗h2s=hr′,此时证明者的秘密输入是r和r′,而验证者通过多项式承诺方案得到v的取值.

3.4 零知识证明方案的具体描述

本小节介绍零知识证明方案的详细过程,其中P是指证明者,V是指验证者.

公开输入:(ck,C,N,m,n),这里ck=(G,q,g,g),g=(g1,g2,···,gn)∈Gn和函数f的布尔电路C.

证明阶段:

如果n=1,将 (pe,r,ρ)发送给 V;

否则计算r′=r◦y′+2s(x),并将 (pe,ρ)发送给 V.

验证阶段:首先V计算v←PolyVerify(pc,pe,x),如果v=⊥则拒绝并验证失败.

•如果n=1,V根据收到的r计算r′=r◦y′+2s(x)并且验证

•如果n>1,P和V运行如下向量内积承诺

(G,g,h,R,R′,v+2K,n/2;r,r′)

这里

引理2给出上述对任意可满足性电路的基于多项式承诺的零知识证明方案的安全性.

引理 2上述对可满足性电路的零知识证明方案满足完美完全性 (perfect completeness)、完美诚实验证者零知识性 (perfect special honest verifier zero-knowledge)以及统计的见证扩展模拟性 (statistical witness-extended emulation),即提取一个违背承诺方案绑定性的实例或者可满足性电路中的见证(witness).

证明请参考文献[19].

4 高效的范围证明方案

范围证明是零知识证明在区块链系统中的一个重要应用.范围证明是指对于某个值v∈[0,2n),证明者构造Pedersen承诺V=gwhv以及相应的证据,以证明该值v确实在范围[0,2n)中.

文献[18]将v按单比特处理,即令,则vi(vi−1)=0,根据这两个方程构造多项式,并利用多项式承诺构造范围证明.最后他们提出的改进的向量内积承诺将证据的长度减为O(logn).本文将v按两比特处理并构造新的多项式,然后构造相应的多项式承诺,最后结合向量内积承诺给出高效的范围证明方案.

4.1 新方案描述

令v=,这里k=n/2.此时vi(vi−1)(vi−2)(vi−3)=0.令

a=(v0,v1,···,vk−1),

b=a−3,c=a◦b,d=c+2,

v=a·t4

这里定义

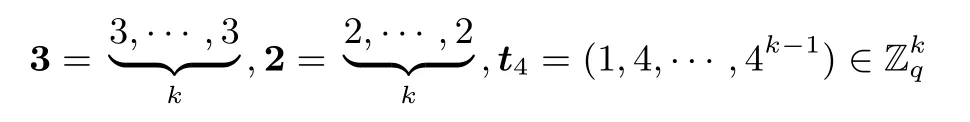
按照前面介绍的方法,我们构造两个洛朗多项式r(X)和r′(X),使得这两个向量多项式的乘积多项式的常数项为零,即令

r(X)=ay−1X+bX−1+cX2+dX−2+cy−1X3+eX4

s(X)=y·y2k·(yX−1−X+ykX−2−ykX2)+t4yX−1−2y′X−3

r′(X)=r(X)◦y′+s(X)

t(X)=r(X)·r′(X)−K(y)

这里y=(y,y2,···,yk)∈Zkq,y′=(y2,y4,···,y2k)∈以及K(y)=y2k·y·(3+2yk).于是t(X)的常数项

t0=2(a◦b−c)·y′·y−1+2(c◦d)·y′+y·y2k((a−b)+(c−d)·yk)+(a·t4)−K(y)

=y2k·y·(3+2yk)+v−K(y)=v

在介绍协议的执行过程之前,令该协议的公开参数 (G,q,g,h,gs,hs,gu,g,h),这里g=(g1,g2,···,gk),h=(h1,h2,···,hk),且g,h,g,h,gs,hs,gu的离散对数互不知晓.下文的过程描述中P是指证明者,V是指验证者.

证明过程:

•P→V: 随机选择α,β,γ,δ,θ∈以及盲化向量 e∈,计算

A=Comck(a;α),B=Comck(b;β),C=Comck(c;γ),

D=Comck(d;δ),E=Comck(e;θ)

这里ck={G,q,g,g},然后将A,B,C,D和E发送给验证者.

•P←V:发送随机值y∈,然后 P计算s(X)和K(y)

•P→V:P计算洛朗多项式

r(X)=ay−1X+bX−1+cX2+dX−2+cy−1X3+eX4

s(X)=y·y2k·(yX−1−X+ykX−2−ykX2)+t4yX−1−2y′X−3

r′(X)=r(X)◦y′+s(X)

t(X)=r(X)·r′(X)−K(y)

然后对t(X)的非零系数做承诺,即,这里t(X)=

i∈{−5,−4,−3,−2,−1,1,2,3,4,5,6}.P 将这 11个承诺值发送给 V.

•P←V:发送随机值x∈,V计算

s=s(x)=y·y2k(yx−1−x+ykx−2−ykx2)+t4yx−1−2y′x−3

•P→V:P计算

r=r(x)=ay−1x+bx−1+cx2+dx−2+cy−1x3+ex4

ρ=αy−1x+βx−1+γx2+δx−2+γy−1x3+θx4

s=s(x)=y·y2k·(yx−1−x+ykx−2−ykx2)+t4yx−1−2y′x−3

以及t=t(x)=r·(r◦y′+s)和τx=,这里τ0=ω,即承诺值V的随机指数.如果k=1,P将τx,ρ,r发送给 V;否则 P将τx,ρ,t发给V.

验证过程:首先验证者根据收到的τx和t验证是否成立,如果不成立,则验证失败.其次,

•如果k=1,V根据r计算t=r·(r◦y′+s)−K(y)并验证

Comck(r;ρ)=Ay−1xBx−1Cx2Dx−2Cy−1x3Ex4

是否成立,如果不成立,则验证失败.

•如果k>1,P 和 V 均计算R=Ay−1xBx−1Cx2Dx−2Cy−1x3Ex4g−ρ=gr并计算

(G,q,gu,gv,hv,R′,k;r,r′)

本节给出的范围证明方案是交互式方案,为了将其应用在区块链系统中,利用Fiat-Shamir变换很容易将其变为非交互式范围证明方案.

定理1本文提出的范围证明方案具有完美完整性(perfect completeness)、完美诚实验证者零知识性(perfect honest verifier zero-knowledge)以及计算特殊合理性(computational special soundness).

证明:证明者和验证者在运行向量内积承诺之前,他们的交互过程与文献[19]中的对可满足性电路的零知识证明方案的过程一致.如果证明者和验证者不运行向量内积承诺,而是证明者在最后一步将t(X)的承诺以及r直接发送给验证者,根据引理1和多项式承诺的完美完整性和统计特殊合理性 (statistical special soundness),该修改的范围证明方案具有完美完整性、完美诚实验证者零知识性以及计算特殊合理性.而本文提出的范围证明方案是将向量内积承诺替换这个修改范围证明方案的最后一步,由于gu,g,h的离散对数互不知晓,根据引理2以及类似文献[18]对计算特殊合理性的证明,本文提出的范围证明方案具有完美完整性、完美诚实验证者零知识性以及计算特殊合理性.

4.2 新方案性能分析

本文我们只考虑将G上的指数运算作为对范围证明方案的计算复杂度的估计,这是因为Zq上的算术运算与G上的指数运算相比可以忽略不计.记ct为G上随机元素的指数运算所需的时间复杂度,指数运算由平方和乘法运算组成.本文假设指数运算所需的总平方运算和总乘法运算耗时相当,并且假设固定元素的指数运算所需要的时间复杂度只占随机元素指数运算时间复杂度的一半 (这里暂不考虑建表等优化细节).设cs为G上元素的长度并且假设G中元素和Zq中元素的比特长度相同(如果考虑G为椭圆曲线群,利用点压缩技术后,G中元素只比Zq中元素多1比特).

下面分析本文方案的计算复杂度和证据长度.在运行内积向量承诺(G,q,gu,gv,hv,R′,k;r,r′)之前,证明者的计算开销主要是 (A,B,C,D,E)的计算、11个Ti的计算以及 (gv,hv,R′)的计算,其总的时间复杂度约为 (0.75n+19)ct,而验证者的计算开销主要是 (τx,t)的验证以及 (gv,hv,R′)的计算,其总的时间复杂度约为 (0.5n+12)ct.证明者和验证者运行内积向量承诺 (G,gu,gv,hv,R′,k;r,r′)所需的时间复杂度分别为 (0.5n+6.5logn−15)ct和 (4.5logn−7)ct.综上,证明者产生证据的时间复杂度为 (1.25n+6.5logn+4)ct,而验证者产生证据的时间复杂度为 (0.5n+4.5logn+5)ct,证据的长度为(19+2logn)cs.

接下来分析文献[18]中方案的计算复杂度和证据长度.在运行内积向量承诺之前,证明者花费的时间复杂度约为(2n+3.5)ct,而验证者花费的时间复杂度约为(n+6)ct.证明者和验证者运行内积向量承诺所需的时间复杂度分别为(n+6.5logn−8.5)ct和(4.5logn−2.5)ct.因此证明者总的时间复杂度约为(3n+6.5logn−5)ct,而验证者总的时间复杂度约为(n+4.5logn+3.5)ct,证据的长度为(9+2logn)cs.

最后分析文献 [16]和文献 [14]方案的计算复杂度和证据长度,并在表2中给出这四个方案的证据生成时间、证据验证时间以及证据长度.值得一提的是,文献[16]方案需要可信第三方的预计算,且预计算的时间复杂度为 (2n/m+0.5)ct,表中ce表示G上的双线性对的时间复杂度,一般来说ce>8.5ct.本文与文献[18]相比,证据生成的时间和证据验证的时间均大大减少.

从表中可以看出,在无中心的前提下,本文的方案是非常有优势的.值得一提的是,工程实现一般选择G为满足离散对数困难的素数阶椭圆曲线群,则文献[14,18]以及本文所提出的方案具有很大的优化空间,而文献 [16]方案中证据的真实生成时间不会比本文方案的证据生成时间要少.考虑到本文的方案在验证的时间复杂度上更有优势以及证据长度很小,本文的方案更适合应用在区块链系统中.

表2 范围证明方案的性能比较Table 2 Performance comparison among range proof schemes

5 结论

本文研究文献[18]的范围证明方案并结合该文献的零知识证明方案提出一种新的高效的范围证明方案,新方案对金额进行两比特分割,然后结合向量内积承诺构造相应的多项式承诺.与文献[18]中的方案相比,当范围区间为[0,264)时,本文的方案将证明者的计算时间减少了近一半,而将验证者的计算时间减少约33%.通过与文献[14,16,18]的方案相比,本文的方案非常实用.