向量等分量数的两方保密计算及推广应用*
王颖囡,窦家维,葛 雪
陕西师范大学数学与信息科学学院,西安710119
1 引言
向量是既有大小又有方向的量,可以用来解决许多科学技术问题与实际应用问题.在数学中,可由向量的点积(叉积)是否为零来判定两直线是否正交(平行).在物理学中力和速度的分解及求和也都离不开向量运算.同时,向量在选举、信息推荐等方面也有着重要的应用.在选举过程中,把全体候选人的得票数记为向量,便可以解决复杂的选举问题.同样地,在进行信息推荐时,可以把用户的有用信息表示成向量,将其与商品信息组成的向量进行对比并计算匹配性,从而为用户推荐最可能需求的商品.但在进行各种向量计算时,保护用户的隐私也尤为重要.比如,在人们收到推销电话时会考虑自己的需求与手机号码在何时已泄露出去,同样,在检测一篇很有价值的论文的重复率时,用户会担心自己的成果会不会在检测过程中被剽窃.为了在保护隐私的条件下解决上述问题,就需要将其转化为有关的向量安全多方计算问题来解决.
安全多方计算是指多个持有私有数据的参与者在保证其私有数据安全性的基础上,利用这些私有数据共同参与某些联合计算,得到参与者想要计算的结果.安全多方计算是由姚期智教授[1]首次提出的,Goldreich,Micali等人[2–5]对其进行了深入的研究,使其发展成为计算机科学中必不可少的组成部分,也成了信息安全的理论基础.目前,在安全多方计算方面,人们研究了各种各样的问题,包括保密的信息比较[6–8]、集合问题[9–12]、保密的计算几何[13–16]、保密的数据挖掘[17]等.
目前,有关向量的安全计算问题的研究有向量的求和[18,19]、向量的线性组合[20]、向量内积的计算[21,22]、向量优势的判定[4,23].文献 [18]对向量的求和问题进行了研究,用 Paillier加密方案将每个向量进行加密并利用其具有的加法同态性得到向量和的密文,为了抵抗合谋攻击,借助可信的第三方将解密密钥拆分给多个权威中心,并由权威中心联合解密得到所需结果.但由于加密次数过多,解密又要借助难以找到的可信第三方,协议的实现性较差.文献[19]应用改进的ElGamal加密系统设计向量求和协议,但由于改进的ElGamal加密系统把要加密的消息放在指数上,解密时会涉及到求解离散对数问题,而由于计算离散对数问题的困难性,协议不能完全解密,最终需要通过穷举法等方法来获得明文,计算效率较低.文献[20]利用NTRU公钥加密和 ElGamal加密实现了向量线性组合的保密计算,并在此基础上解决可抵抗量子攻击的多项数据安全统计问题和选举问题.文献[21,22]研究了向量内积的保密计算.文献[4]首次提出安全向量优势问题,借助百万富翁协议对于向量中对应分量分别进行大小比较,效率较低.文献 [23]应用适当的编码方法解决了安全向量优势问题,并以此为基础研究了整除问题以及点与若干直线位置关系判定问题.
在对事物进行分析与研究时,通常会把有关研究对象的重要特征提取出来用一个向量表示,并根据向量之间的匹配程度对研究对象进行分类、聚类,进而研究其性质.向量的匹配程度可以应用向量中对应分量相等的分量个数来衡量,而相等分量数目计算问题可看成海明距离的推广.文献 [24]主要研究了海明距离及其一些推广应用问题的保密计算,其中,binHDOT协议研究了半诚实模型下两方参与者对其具有的比特字符串海明距离的保密计算 (参看文献 [24]的 Figure 1),以 binHDOT协议为基础,HDOT协议进一步研究了由任意字符数据构成的字符串的海明距离 (参看文献 [24]的 Figure 2),HDOT协议的设计思想是两方参与者首先将其具有的字符串中各个字符数据表示为具有相同长度的二进制串,进一步以binHDOT协议为基础对变换后的二进制串逐对进行相等判定,最终获得两字符串的海明距离(字符串中对应字符数据不相等的字符数目).如果将HDOT协议中两方字符串中各个字符数据看作一个向量的分量,则可以直接应用文献[24]的HDOT协议解决两个向量的等分量数问题.但由于在文献[24]的HDOT协议中需要多次调用两比特串海明距离计算协议,协议复杂性较高.本文主要对于向量等分量数保密计算问题设计高效的保密计算协议(文献[24]中HDOT协议与本文协议的效率比较将在第5节详细讨论).
本文主要贡献如下:
(1)应用新的方法解决向量等分量数保密计算问题.分别设计了对向量数据有全集限制以及无全集限制情形下向量等分量数保密计算协议,应用模拟范例方法严格证明了所设计的协议在半诚实模型下是安全的.
(2)进一步设计了向量等分量数阈值问题的保密判定协议和向量优势统计方案.
(3)本文协议可以作为构建其他安全多方计算问题协议的基本模块,用于解决其他很多安全多方计算问题,文中给出了一些具体的应用举例.
本文组织如下:第2节介绍了本文需要用到的一些预备知识;第3节设计了有全集限制和无全集限制条件下向量等分量数计算协议,并严格证明了协议的安全性;第4节主要研究向量等分量数阈值问题保密判定和向量优势统计问题;第5节分析了本文协议的复杂度,并对具体计算问题进行实验测试;第6节给出了向量等分量数计算协议在解决实际问题中的两个具体应用;第7节对全文进行总结.
2 预备知识
2.1 安全性定义
理想模型m个参与者P1,···,Pm,分别把私密数据x1,···,xm发送给一个可信的第三者TTP,TTP计算函数f(x1,···,xm)=(f1(x1,···,xm),···,fm(x1,···,xm)),将结果fi(x1,···,xm),i∈[1,m]={1,2,···,m}分别发送给参与者Pi.参与者Pi在协议中除了获得规定的输出结果fi(x1,···,xm)外,得不到其他参与者数据的任何额外信息.这样的安全计算模型称为理想模型.
由于在任何情况下,TTP都不会泄露任何不该泄露的信息,因此理想模型下的计算协议是安全性最高的多方计算协议,由于理想模型有赖于TTP,而在实际中要找到一个可信的第三方并非易事,因此需要设计不依赖于TTP的实际安全计算协议,通过和理想协议进行比较来检验实际计算协议的安全性.
半诚实模型所谓半诚实参与者是指那些在协议执行过程中按照协议要求忠实地履行协议的参与者,但他们可能会收集和保留在协议执行过程中获得的所有信息,在协议执行后试图根据这些信息推算出其他参与者数据的额外信息.如果所有参与者均为半诚实参与者,称这样的计算模型为半诚实模型[3].文献[3]给出了一个将半诚实模型下安全协议直接编译成恶意模型下安全协议的一般方法,因此设计半诚实模型下安全计算协议是基本而重要的.本文主要研究半诚实模型下的两方向量保密计算问题.
安全性定义假设有概率多项式时间函数f(x,y):(x,y)→(f1(x,y),f2(x,y)),π为计算函数f的一个两方协议.记协议的参与者为 Alice和 Bob,他们的输入分别为x,y,协议执行中 Alice得到的信息序列记为其中r1为 Alice选择的随机数,为 Alice收到的第i个信息,f1(x,y)为 Alice获得的输出结果,类似定义 Bob在协议执行中得到的信息序列为
如果存在概率多项式时间算法S1,S2,使得下面两式成立
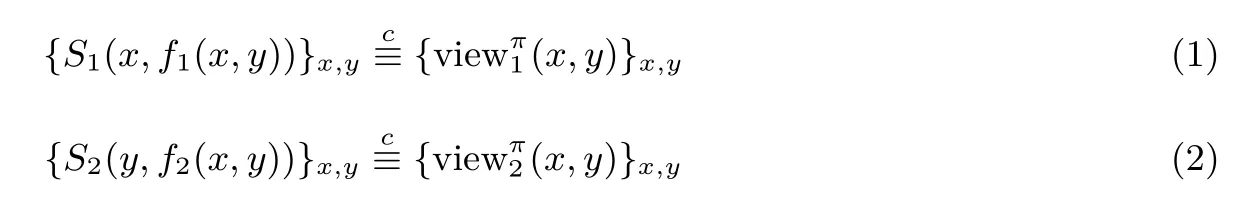
则称协议π安全地计算了函数f.其中表示计算上不可区分.要证明一个两方计算协议是安全的,就必须构造满足式(1)和式(2)的模拟器.这种证明安全性的方法是多方保密计算中普遍接受的模拟范例方法.若在协议执行中某参与方未获得任何输出,约定该参与方的输出为空串λ.
2.2 Paillier加密方案
Paillier加密方案具体过程如下[25]:
密钥生成选取大素数p,q,并令N=pq,ω=lcm(p−1,q−1).设函数L(x)=,随机选取g∈满足gcd(L(gωmodN2),N)=1,则公钥为pk=(g,N),私钥为sk=ω.加密算法和解密算法分别记为E和D.
加密对于明文m∈ZN,选择随机数r∈,计算密文c=E(m)=gmrNmodN2.
解密对于密文c∈,解密得到明文m=D(c)如下:

加法同态性由于E(m1)E(m2)=gm1+m2(r1r2)NmodN2=E(m1+m2),因此Paillier加密方案具有加法同态性.
密文重随机化假设E(m)是应用公钥pk加密m得到的一个密文,给E(m)乘上0的一个密文后,得到C=E(m)E(0),根据Paillier加密方案的加法同态性,可知C为m的一个新的密文形式.这个过程称为密文的重随机化.
Paillier加密方案是语义安全的.一个密码系统是语义安全的,意味着同一明文可以加密成多个不同的密文形式,并且这些密文都是计算不可区分的.在下文中,以 Paillier加密方案为基础所做的密文乘积运算和模乘运算均是在模N2的意义下进行的.文中E(−m)=E(N−m),m>0代表−m的密文.
3 向量等分量数保密计算
问题描述:对于两个n维向量U=(u1,···,un),V=(v1,···,vn),定义函数ϕi=Φi(ui,vi):如果ui=vi,则ϕi=1;否则ϕi=0.定义两向量U,V的等分量数为ϕ=Φ(U,V)=Φi(ui,vi).
假设Alice和 Bob各自拥有保密的n维向量U和V,他们希望在不泄露各自隐私数据的条件下合作计算向量等分量数ϕ=Φ(U,V).即他们希望保密计算两个向量中具有性质ui=vi,i∈[1,n]的分量数目.
3.1 向量等分量数保密计算协议1
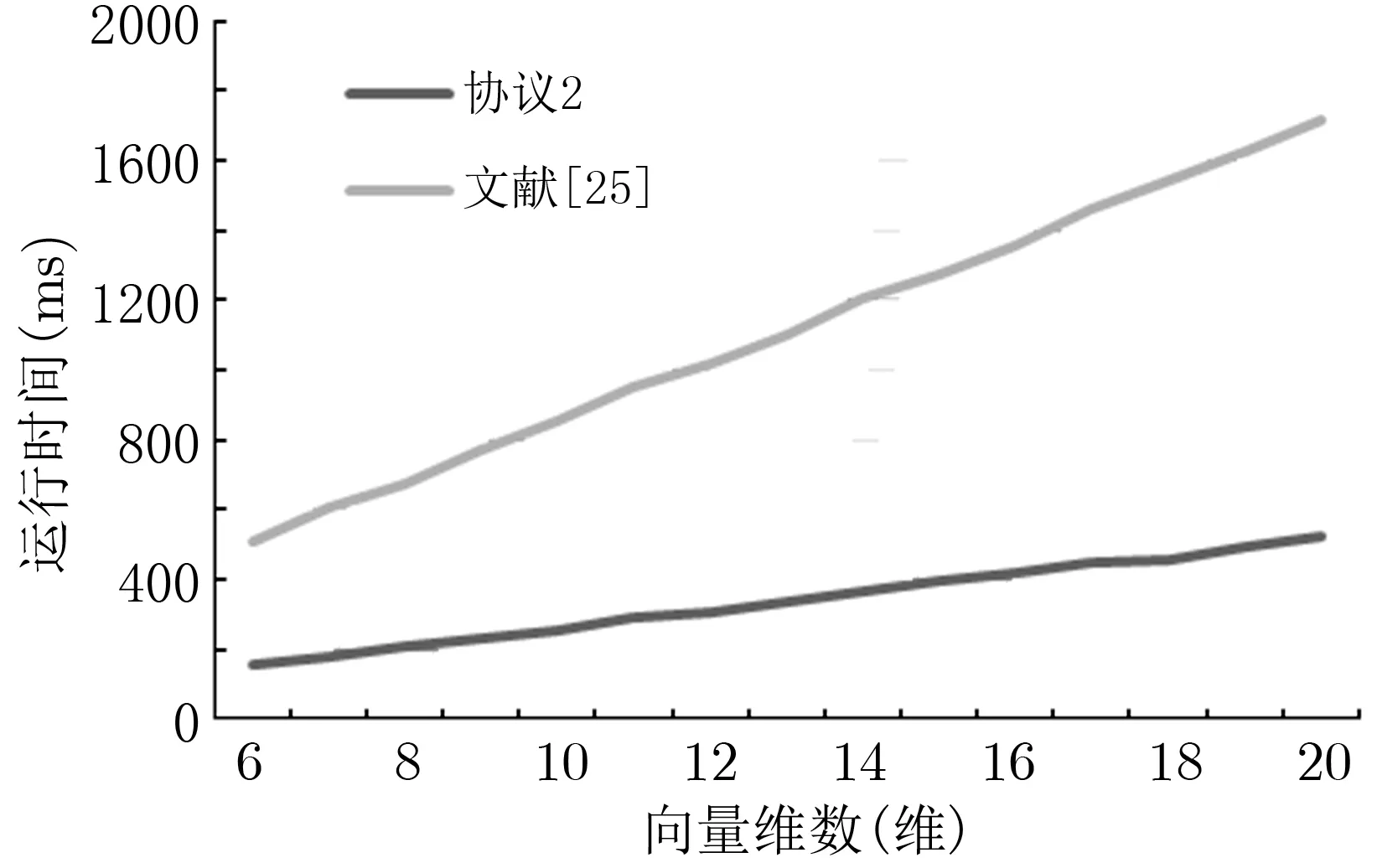
本节主要研究在有全集限制条件下两向量等分量数保密计算问题.即假设在保证参与者输入数据隐私的前提下,参与者双方可以商定一个全集,记为Q={q1,q2,···,qm},满足q1<··· 假设参与者的集合U与V都含于全集Q中,并假设ui∈U以及vi∈V在Q中的序位分别为ki以及li. 编码方法 1Alice对向量U进行编码,编码结果是一个矩阵,记为WU=(uij)n×m,其中uij(i∈[1,n],j∈[1,m])定义如下:如果t=ki,令uit=1;否则,令uit=0. 选择方法对于每一个i∈[1,n],Bob在WU的第i行中选择第li列元素uili,Bob再将所选择的元素相加,得到ϕ=u1l1+···+unln,ϕ即为两向量对应分量相等的数目. 例 1对于向量U=(7,3,0,5,3),V=(5,3,0,6,5),根据全集Q={0,1,2,3,4,5,6,7,8},对U进行编码得到矩阵 由于v1=5,在Q中的序位为6,因此,Bob在矩阵的第1行选择元素u16=0,同理,在矩阵的第2–5行分别选择元素u24=1,u31=1,u47=0,u56=0,这五个元素的和为2,因此向量U,V等分量数为ϕ=2. 为了进行保密计算,我们结合Paillier加密方案实现上述计算过程,具体协议如下: 协议 1:两向量等分量数保密计算协议1. 输入:Alice输入向量U=(u1,···,un),Bob输入向量V=(v1,···,vn),其中ui,vi∈Q. 输出:满足ui=vi,i∈[1,n]的分量数目ϕ=Φ(U,V). 准备工作:(a)Alice运行Paillier同态加密方案,生成私钥sk和公钥pk,将公钥发送给云,并借助云生成若干个0的密文与1的密文,将生成的0与1的密文集合分别记为H0与H1;根据密文重随机化原理,Alice适当选择H0以及H1中不同的密文进行模乘运算,生成两个分别由0和1的密文构成的新集合中至少包含n(m−1)个0的密文,中至少包含n个1的密文,对于云来说(或)中的元素与随机数不可区分). (b)Alice按照编码方法1,对向量U进行编码,得到编码矩阵WU=(uij)n×m,并应用中0与1的密文构造加密矩阵 (1)Alice将公钥pk=(g,N)以及E(WU)发送给Bob. (2)对于每一个i∈[1,n],Bob根据vi在全集Q中的序位li,在矩阵E(WU)第i行挑选第li列元素E(uili).并计算将C发送给Alice. (3)Alice解密C,得到ϕ=D(C)并输出ϕ. 协议1的正确性根据Paillier加密算法的加法同态性,在协议1第2步中,=E(),因此在第3步Alice对C解密后,结果为D(C)=.根据计算原理所述,这正是协议规定的输出结果,因此协议1是正确的. 协议 1的安全性关于协议1的安全性,我们有下面的定理. 定理 1两向量等分量数保密计算协议1在半诚实模型下是安全的. 证明:下面将应用多方保密计算中普遍接受的模拟范例方法严格证明定理1. 首先构造S1.S1接受到输入(U,f1(U,V)=Φ(U,V))后,按如下方式运行: 在协议 1中由于Bob没有利用云进行任何计算,即使Alice和云合谋也无法获得Bob数据的任何额外信息. 下面构造S2.S2接受到输入(V,f2(U,V)=Φ(U,V))后,按如下方式运行: 因此,协议1在半诚实模型下是安全的. 上节中讨论了在数据范围已知的情况下两向量等分量数保密计算问题,但如果集合数据范围不好确定(或范围很大),这时将无法应用上节的协议进行计算(或应用上节协议计算复杂性将很高),因此需要在无全集限制条件下,构造两向量等分量数保密计算协议. 计算原理将向量U,V的对应分量ui,vi,i∈[1,n]逐对进行大小比较,检查其是否相等,并以Paillier加密算法为基础实现保密计算. 协议 2:向量等分量数保密计算协议2. 输入:Alice 输入向量U=(u1,···,un),Bob 输入向量V=(v1,···,vn). 输出:满足ui=vi,i∈[1,n]的分量数目ϕ=Φ(U,V). 准备工作:Alice运行Paillier加密方案,生成加密的公钥pk=(g,N)和对应的私钥sk=ω(可取N足够大使得 (1)Alice加密向量U,得到E(U)=(E(u1),···,E(un)),并将E(U),pk发送给 Bob. (2)对于每一个i∈[1,n],Bob加密−vi,得到E(−vi),并选择随机数ri,0≤ri<计算ci=(E(ui)E(−vi))ri.将c=(c1,···,cn)中分量进行随机置换 (将置换记为π),置换后得到=(cπ(1),···,cπ(n))(其中{π(1),···,π(n)}={1,···,n}),Bob将发送给Alice. (3)对于每一个i∈[1,n],Alice解密ci得到明文di,将 (dπ(1),···,dπ(n))中取值为 0的分量数目记为ϕ,并输出ϕ. 协议 2的正确性根据Paillier加密算法的加法同态性,对于任意i∈[1,n],ci=(E(ui)E(−vi))ri=E(ri(ui−vi)),解密后可得di=ri(ui−vi)modN,由于0≤ri,ui,vi<故−N 协议 2的安全性下面分别考虑Alice和Bob数据的安全性. Alice数据的安全性.由于在协议执行中,Bob仅接收到Alice发送的数据E(U),由于E(U)是Alice加密的密文,Bob没有解密密钥,根据 Paillier加密算法的语义安全性,对 Bob来说从E(U)中得不到Alice数据的任何信息.因此Alice的数据是安全的. Bob数据的安全性.由于在协议执行中,Alice仅接收到Bob发送的密文数据ci=(E(ui)E(−vi))ri(i∈[1,n]).由于E(−vi)是Bob加密的密文,ri为Bob选择的随机数,根据Paillier加密算法的语义安全性以及ri的随机性,对Alice来说从ci(i∈[1,n])中得不到Bob数据的任何信息.虽然Alice有解密密钥,解密后Alice仅获得(dπ(1),···,dπ(n))中哪些分量为0,由于Alice不知道将c转化为的随机置换π,即Alice不知道π(i)和i的对应关系,因此Alice无法获知对于具体哪些i∈[1,n],有ui=vi.而当uivi时,di=ri(ui−vi)modN,因ri是 Bob选择的随机数,故Alice从协议 2的执行中得不到Bob向量数据的任何额外信息.因此,Bob的数据是安全的. 类似于定理1,可以通过构造模拟器S1,S2严格证明协议2的安全性.仅叙述下面定理,证明从略. 定理 2两向量对应分量相等个数保密计算协议2在半诚实模型下是安全的. 问题描述Alice和 Bob分别具有向量U=(u1,···,un)和V=(v1,···,vn),并事先商议好全集Q和阈值k(1≤k≤n),使得对于所有i∈[1,n],ui,vi∈Q.Alice和Bob希望保密判定两向量分量相等个数ϕ=Φ(U,V)与阈值k的大小关系,而不泄露关于集合U,V的任何额外信息. 计算原理Alice和Bob首先以协议1为基础获得函数值ϕ的密文,这时不需要解密,进一步结合k的密文来保密判定Φ(U,V)与k的大小关系. 为叙述方便,定义谓词:h=Hk(U,V):如果Φ(U,V)≥k,定义h=1,否则,定义h=0.为了构造本节的保密计算协议,我们需要解决两个数大小的保密判定问题.首先证明下面命题. 命题 1假设 Paillier加密系统中私钥为 sk,公钥为 pk=(g,N),加解密算法分别为E,D.任意0≤u,v 证明:按照Paillier加密算法的定义以及加法同态性,C=E(u)E(−v)=E(u−v),对C应用私钥sk进行解密,解密结果为w=D(C)=(u−v)modN. (a)当u=v时,得到w=D(C)=(u−v)modN=0. (b)当u>v时,此时由于0 (c)当u 由于w=D(C)=(u−v)modN∈ZN,根据假设条件0≤u,v 命题 2对任意整数a,b,a≥b当且仅当2a+1>2b;a>b当且仅当2a>2b+1. 证明:若a≥b,则 2a≥2b,因此 2a+1>2b.反之,若 2a+1>2b,则必有 2a≥2b成立,即a≥b成立.综上,a≥b当且仅当2a+1>2b.同理可得a>b当且仅当2a>2b+1. 下面给出具体协议. 协议 3:向量等分量数阈值问题保密判定协议. 输入:Alice输入向量U=(u1,···,un),Bob输入向量V=(v1,···,vn),对于所有i∈[1,n],ui,vi∈Q. 输出:向量等分量数Φ(U,V)与阈值k的大小关系h=Hk(U,V). 准备工作:协议3准备工作与协议1相同. (1)Alice将公钥pk=(g,N)以及E(WU)发送给Bob. (2)对于每一个i∈[1,n],Bob根据vi在全集Q中的序位li,在矩阵E(WU)第i行挑选第li列元素E(uili).Bob选择随机数r满足并将C发送给Alice. (3)Alice解密C得到c,若,令h=1,否则令h=0.输出h. 协议 3的正确性:协议3的准备工作和第(1)步与协议1完全相同.在协议3第(2)步,Bob首先计算得到ϕ的密文:此后计算因此在第 (3)步中,解密结果c=r(2ϕ+1−2k)modN,由于 0≤ϕ,k≤n,r<,故可得 0≤r(2ϕ+1),2rk 协议 3的安全性下面分别考虑Alice和Bob数据的安全性. Alice数据的安全性.在协议执行中,Alice仅给Bob发送了密文数据E(WU).由于Bob没有密钥,根据Paillier加密系统的语义安全性,Bob由E(WU)得不到Alice数据任何额外的信息,因此Alice数据是安全的. Bob数据的安全性.在协议执行中,Bob仅给Alice发送了密文由于r是Bob选择的随机数,并且E(−2k)是Bob加密的密文,根据Paillier加密算法的语义安全性,对Alice来说从密文C中得不到Bob数据的任何信息.虽然Alice有解密密钥,解密后Alice仅获得h的值,该值是协议规定的输出数据,因此Bob数据是安全的. 类似于定理1,可以通过构造模拟器S1,S2严格证明协议3的安全性.仅叙述下面定理,证明从略. 定理 3向量等分量数阈值保密判定协议3在半诚实模型下是安全的. 在文献 [23]中,通过对数据编码研究向量优势问题,向量优势问题是指:Alice有向量U=(u1,···,un),Bob有向量V=(v1,···,vn).Alice和 Bob希望在不泄露各自向量信息的基础上统计出满足ui>vi,i∈[1,n]的分量个数T(U,V),而不泄露关于集合U,V的任何额外信息. 基本原理如下:Alice和 Bob事先商议好元素的全集Q,使得对于所有i∈[1,n],ui,vi∈Q.设向量U中的元素ui位于全集Q中的第ki位,向量V中的元素vi位于全集Q中的第li位.Alice对私有向量U进行编码,得到矩阵 (SU)n×m,其中元素uit定义如下:当t≤ki时uit=0;当t>ki时uit=1(记该编码方法为编码方法2).对于i∈[1,n],Bob在SU的第i行中挑选第li位元素uili并相加,即得到 考虑到在一些应用场景下,仅仅统计优势分量数目并不能达到要求,为了进一步拓宽原有协议的应用范围,下文中将向量优势统计与阈值进行结合,解决向量优势阈值统计问题. 问题描述Alice有向量U=(u1,···,un),Bob有向量V=(v1,···,vn),并事先商议好阈值k,1≤k≤n和全集Q,使得对于所有i∈[1,n],ui,vi∈Q.Alice和Bob希望在不泄露各自向量信息的基础上统计出ui>vi,i∈[1,n]的个数T(U,V)与k的大小关系,而不泄露关于集合U,V的任何额外信息. 我们以上述计算原理及 Paillier加密算法为基础,进一步讨论向量优势阈值问题.首先计算T(U,V)的密文,进一步结合k的密文,根据命题1,2来保密判定T(U,V)与k的大小即可.为描述方便,定义谓词:l=Lk(U,V):如果T(U,V)≥k,定义l=1,否则,定义l=0.具体协议设计如下: 协议 4:向量优势阈值问题保密判定协议. 输入:Alice输入向量U=(u1,···,un),Bob输入向量V=(v1,···,vn),对于所有i∈[1,n],ui,vi∈Q. 输出:满足ui>vi,i∈[1,n]的元素个数T(U,V)与k的大小关系l=Lk(U,V). 准备工作:(a)Alice运行Paillier加密方案,生成私钥sk和公钥pk. (b)Alice按照编码方法2,对向量U进行编码,得到编码矩阵SU=(uij)n×m,借助云生成多个0,1的密文(其中0,1的密文不少于SU中0,1个数).并用云生成的数据本身对所有密文进行重随机化(参看协议1准备工作),借助随机化后的云生成的密文构造加密矩阵 (1)Alice将公钥pk=(g,N)以及E(SU)发送给Bob. (2)对于每一个i∈[1,n],Bob根据vi在全集Q中的序位li,在矩阵E(SU)第i行挑选第li列元素E(uili).Bob选择随机数r满足r<,计算,并将C发送给Alice. (3)Alice解密C得到c,若c<,令l=1,否则令l=0.输出l. 协议 4的正确性与安全性协议 4是在文献[23]计算结果的基础上进一步应用命题 1判定T(U,V)与k的大小关系,其正确性与安全性证明与协议3类似,此处省略. 由于文献[23]给出的协议要求向量分量在某个全集内取值,且随着全集的增大,协议的效率也随之降低.因此需要设计在没有全集限制情况下的计算协议.下文以命题1,2与协议2为基础设计无全集限制情况下的向量优势统计协议. 协议 5:向量优势统计协议. 输入:Alice输入私密向量U,Bob输入私密向量V. 输出:满足ui>vi,i∈[1,n]的元素个数t=T(X,Y). 准备工作:Alice计算xi=2ui,Bob计算yi=2vi+1.Alice运行 Paillier加密方案,生成公钥pk=(g,N)与私钥,并公布公钥(可取N足够大,使得所有 (1)Alice 加密向量X=(x1,···,xn)(逐项加密), 得到E(X)=(E(x1),E(x2),···,E(xn)), 将E(X)发送给Bob. (2)(a)Bob 加密向量−Y=(−y1,···,−yn)(逐项加密), 得到E(−Y)=(E(−y1),E(−y2),···,E(−yn)); (b)Bob选择随机数ri (c)Bob将W中元素进行随机置换,得到=(wk1,wk2,···,wkn),并将发送给Alice. 协议5的正确性与安全性与协议2类似,不再具体论证. 本文协议效率分析本文所用的协议都是在Paillier加密算法的基础上进行的,在进行计算复杂度分析时,为了便于比较,我们忽略模乘运算,只考虑最耗时的模指数运算.Paillier加密方案中加密1次需要2次模指数运算,解密1次需要进行1次模指数运算.记参与运算的向量维数为n,本文协议效率分析如下. 协议1为全集已知时的计算方法.在协议1中,因加密数据都为0,1,我们借助云外包生成所需要的0,1密文,于是协议的计算复杂度仅仅为1次解密与1次加密的复杂度,即3次模指数运算.协议2为全集未知时的计算方法.在协议2中,Alice进行n次加密和n次解密运算,Bob进行n次加密和n次模指数运算.因此协议2相当于进行6n次模指数运算. 通信复杂度一般由交换信息的通信比特数或者通信轮数来衡量,在安全多方计算中通常用轮数来衡量,每个参与者发送一次消息称为一轮.协议2进行了1轮通信.协议1在执行过程中借助云生成多个密文供参与者使用,因此其通信复杂性为 2轮,Alice和 Bob之间进行了1轮通信,Alice和云之间也进行了1轮通信. 综上可得,在只考虑模指数运算的情况下,协议1的计算复杂性很低,但协议1的使用前提是元素范围已知,且在执行过程中借助了云进行计算,通信代价较高.而当向量中数据的范围较大时,用协议2进行计算就更为方便. 协议3给出了向量等分量数阈值问题计算方法.在协议3中,前两步和协议1相同,都为对0,1的加密,考虑外包时忽略其计算复杂度,在协议的后两步,共进行了2次加密,2次模指数和1次解密运算,因此协议3相当于进行7次模指数运算.其通信复杂度也等同于协议1,共进行了2轮通信. 协议4解决的是向量优势阈值问题保密判定,是基于阈值的向量对应分量相等个数判定问题的推广,与协议3相比仅改变了原始数据的编码方法,其计算复杂性和通讯复杂性都等同于协议3.协议5将协议2进行扩展,计算无全集限制下的向量优势统计问题,其计算复杂性与通讯复杂性等同于协议2.故在此不作考虑. 与已有相关结果进行分析比较文献 [24]中的 HDOT协议能够解决字符串海明距离保密计算问题(执行 HDOT协议的前两步),如果将字符串中的各个字符看成向量的不同分量,则可应用文献 [24]的HDOT协议解决本文的向量等分量数计算问题.下面主要对应用文献[24]的HDOT协议解决向量等分量数问题时的计算效率进行分析,并与本文协议1,2的计算效率进行比较. 在应用文献 [24]的 HDOT协议计算两字符串的海明距离时 (仅需要执行 HDOT的前两步),如果将输入的字符串中的每个字符数据所对应的二进制数据长度设为l,当输入字符串所包含的字符个数为n时,协议需要调用n次binHDOT协议,每次调用 binHDOT的目的是判定两个l长的比特字符串是否相等.根据文献[24]中binHDOT协议,执行一次l长的比特字符串相等判定(若两字符串相等,输出0,否则输出1)需要进行l次加密与1次解密运算,2l次模指数运算以及logl次不经意传输.即是说,如果应用文献[24]的HDOT协议(HDOT协议的前两步)保密计算两个n维向量的等分量数问题,需要进行n(4l+1)次模指数运算与nlogl次不经意传输.协议的通信复杂性为O(nl)(这里l为向量分量数据在二进制表示下的数据长度). 表1给出了在解决两个n维向量的等分量数保密计算问题时,应用本文协议 1,2与应用文献[24]中的HDOT协议(HDOT的前两步)的计算效率比较结果. 表1 协议效率分析Table 1 Analysis on efficiency 为进一步分析本文协议的执行效率,我们设计模拟实验来计算执行协议所需时间. 实验测试环境:Windows 10 64位 (家庭版)操作系统,处理器 Intel(R)Core(TM)i5-6600 CPU@3.30 GHz,内存 8.00 GB,用 java语言在 MyEclipse上运行实现.本文所做模拟实验均在此环境下进行. 实验方法:通过模拟实验来测试本文协议所用时间,并通过协议执行时间来验证方案效率.假定本文协议1全集元素个数m=20.在向量维数n分别为6,7,8,···,20时,对n的每个设定值进行100次模拟实验,并统计协议1,2执行时间的平均值与文献[24]中HDOT协议前两步(仅考虑Paillier加密与解密所耗费的时间)的执行时间的平均值. 由于协议1借助云来完成加密过程,协议复杂性较低,且随着向量维数增加,协议运行时间基本不变.经实验,协议1平均一次运行时间为15 ms.协议2与文献[24]中HDOT协议前两步(在l=5时)的运行时间随n的变化如图1所示,在向量维数相同时,本文协议2的执行时间远小于文献[24]的执行时间. 问题描述Alice 有区间列 [a1,b1],···,[an,bn],Bob 有数列v1,···,vn,其中ai,bi,vi,(i=1,2,···,n)为正整数.Alice和 Bob希望在不泄露各自信息的条件下保密计算满足vi∈[ai,bi](i=1,2,···,n)的区间个数. 图1 协议2,文献[24]的执行时间随向量维数增大的变化规律Figure 1 Execution time of Protocol 2 and Ref.[24]with increase of vector dimension 对上述问题设计安全高效的计算协议在实际中有广泛应用.例如:(a)实际中如果需要保密判定一个整数点P(x,y,z)是否含于一个立方体V=[x1,x2]×[y1,y2]×[z1,z2]内.这个问题即可转化为判定三个坐标值是否都分别属于三个对应区间的问题.(b)某公司A希望考察一个公司B,看看能否成为合作伙伴,在确定是否可以合作之前,A需要通过一些指标对B进行考核评估,如考核其公司资产,项目数量,生产能力等是否在要求范围内.由于B的这些指标量属于企业的机密信息,A的指标范围也属于商业机密,为了在保证各企业商业机密的前提下确定能否合作,就需要设计数与区间保密判定协议.(c)又如医学上根据各项指标进行的疾病初步检测,学校根据各科成绩判定优等生等问题,都可以抽象为多个点与区间的关系判定问题. 下面以向量等分量数计算协议为基础,设计多个点与区间的关系判定问题的解决方案. 基本原理记mi=bi−ai,取一整数m>max{m1,m2,···,mn}. (i)对于每一个区间 [ai,bi],将 [ai,bi]转化为向量Ai=(ai,ai+1,ai+2,···,ai+m). (ii)将Ai中大于bi的元素全替换为零,如此得到的向量记为Bi.将B1,···,Bn首尾相连得到一个n(m+1) 维向量B=(B1,B2,···,Bn) (iii)记I是分量全为 1的m+1维向量,即I=(1,1,···,1).令Vi=viI,并将V1,···,Vn首尾相连得到一个n(m+1)维向量V=(V1,V2,···,Vn). 由向量B和V的构造过程容易证明:满足vi∈[ai,bi](i=1,2,···,n)的区间个数即为两向量B和V对应分量相等的分量数目.因此,Alice根据其私有区间序列构造相应的私密向量B,Bob根据其私有数列构造私密向量V.Alice和Bob再分别以向量B和V为输入调用协议1,2即可. 注解 1对于i∈[1,n],以集合Xi={xi1,···,ximi}代替上面问题中的区间 [ai,bi](假设xi1,···,ximi单调递增). 同样选取m>max{m1,m2,···,mn},进一步定义Yi为m+1维向量:Yi=(xi1,···,ximi,0,···,0).再令Y=(Y1,···,Yn).完全类似地,通过计算向量Y与向量V等分量数,可计算有多少个集合满足vi∈Xi. 注解 2对于上述点与区间 (或集合)关系问题,也可以类似考虑其相应的阈值问题,而转化为可以应用协议3解决的计算问题. 字符串模式匹配[26]作为字符串的一项基本操作,在实际生活中有着重要作用.如果把某个地区信誉过低的人的名单整体看成一个字符串,某个居民的名字当作另一个字符串,判定此人信誉是否过低问题就转化为判定两个字符串是否模式匹配问题.显然,信誉过低的人的名单在一些情况下不能直接公开,查询者在查询自己信誉是否过低时也不愿意泄露自己的名字.因此需要保密判定两个字符串是否模式匹配. 问题描述Alice有目标字符串A=a1a2···,an,Bob有模式字符串B=b1b2···,bm(m≤n,m,n为公开值).在不泄露其他任何信息的情况下判断A中是否存在一个子串与B相等,即判定在字符串A=a1a2···an中是否存在子串SA=aiai+1···ai+m−1=B. 基本原理将英文字母与数字做如下对应: a→01,b→02,···,z→26 记ai,bi对应的数字分别为xi,yi,从而将字符串A,B转化为数字串Sx=x1x2···xn,Sy=y1y2···ym.Alice 根据m将Sx分割为n−m+1 维向量X=(x1···xm,x2···xm+1,···,xn−m+1···xn),Bob 根据n将Sy转变为n−m+1 维向量Y=(y1···ym,y1···ym,···,y1···ym). 设置阈值k=1,通过协议3保密判定向量X,Y等分量数与阈值的大小关系即可得到结果:如果等分量数小于阈值,则说明A,B不能模式匹配,否则说明A,B能模式匹配. 本文利用Paillier加密算法和对数据的编码,根据全集是否已知设计了简单的计算两向量等分量数的协议,并证明了协议的正确性和安全性,分析了协议的效率.此外,我们将所设计的基础协议进行延伸,解决了在考虑阈值的情况下的向量等分量数和向量优势统计问题,并设计了无全集限制的向量优势统计协议.同时,利用这些基础协议解决了多个点与区间(集合)的关系判定问题和字符串匹配率计算问题.在后面的工作中,我们将探讨恶意模型下的向量等分量数计算问题.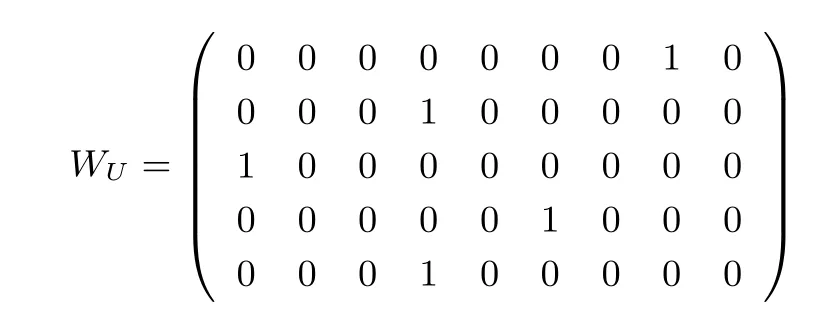


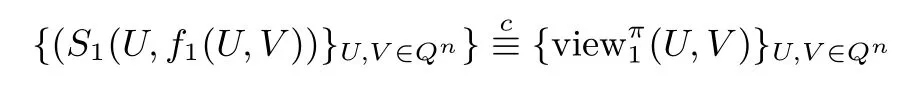


3.2 向量等分量数保密计算协议2
4 向量等分量数扩展问题
4.1 向量等分量数阈值问题
4.2 向量优势及其阈值问题
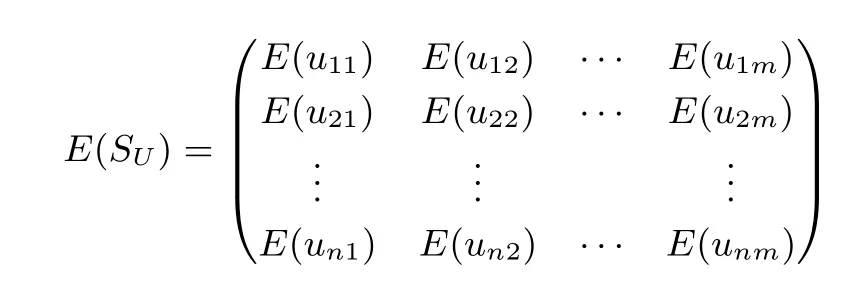
5 协议效率分析与实验数据分析
5.1 效率分析

5.2 实验数据分析
6 向量分量相等个数的应用
6.1 点与区间关系保密计算问题
6.2 字符串匹配字符个数保密计算
7 结论

