基于编织法的de Bruijn序列差异性研究*

王向宇,王中孝

战略支援部队信息工程大学,郑州450001

1 引言

由于de Bruijn序列具有周期最大、元素分布均衡、线性复杂度较高等良好的伪随机性质,因此在序列密码的研究领域中占有重要位置,其中de Bruijn序列的构造问题一直是研究的热点问题之一.文献[1]用组合数学的方法给出一个构造n级de Bruijn序列的算法,即prefer one算法,从而证明了对任意正整数n,皆存在n级de Bruijn序列,但该算法仅能生成一条n级de Bruijn序列.文献[2]用图论的方法证明了全体不平移等价的n级 de Bruijn序列的个数为22n−1−n,但其证明方法不是构造性的.文献[3]总结了de Bruijn序列的构造方法、线性复杂度和重量分布等研究成果.到目前为止,构造de Bruijn序列的方法大致上可分为两类,一类是基于文献[4]中并圈法来构造de Bruijn序列,如文献[5–8].另一类是如文献 [9–11]中体现的利用较低级数 de Bruijn序列构造高级数 de Bruijn序列的递归思想,基于文献[12]中的编织法思想,文献[13]从一条n级de Bruijn序列出发，利用编织法得到两条编织序列,基于该序列的特殊性质,在特定位置上添加4个比特即可构造出四条2n级de Bruijn序列.该算法不仅使得de Bruijn序列级数成倍增长,还能由一条 de Bruijn序列出发构造多条 de Bruijn序列.迭代使用该算法,可以实现de Bruijn序列构造规模的指数级增张.然而,从密码设计的角度来看,除考虑构造所得de Bruijn序列的数量之外,还应当考虑构造所得de Bruijn序列的差异性,这是因为相似的de Bruijn序列往往具有较长的相同序列段,因此在局部上可被视为同一序列,而这应当在实际应用中尽量避免.基于以上考虑,本文主要讨论由一条n级de Bruijn序列出发利用编织法构造所得的四条2n级de Bruijn序列的差异性问题.

本文内容按如下结构进行安排:第2节给出相关定义和准备知识;第3节讨论由编织法所得四条2n级de Bruijn序列的差异性,由于其间的差异性由两条编织序列的差异性唯一决定,而编织序列的差异性又可以转化为两个指定映射的差异性.映射的差异性问题进一步可归结为对n长状态来源的研究,最终本文得到两个映射出现差异的充要条件,进而得到这两个映射的差异数和差异率;第4节对本文进行了总结并指出后续工作.

2 准备知识

本文所讨论序列皆为2元序列,设n是一个正整数,用F2表示二元域,用表示F2上的n维向量空间,文中模运算皆取最小非负剩余.

2.1 周期序列及状态的位置

定义 1[14]对于序列=(a0a1a2···),如果存在一个正整数l满足

al+k=ak,k=0,1,2,···

则称是一个周期序列.满足上式的全体l中的最小正整数称为的周期.此外若无特别说明,本文所讨论的周期序列用该序列的第一个周期表示.

定义2对于任意一条周期为T的序列,将其重复m次可以得到一条新的序列,对序列的这一操作称为m次复写,并将m次复写的结果记作.复写序列用该序列的前mT个比特表示.

定义3对于周期序列=(b0b1···bT−1),称bi为序列的第i位,i=0,1,···,T−1,若r长状态(s0s1···sr−1) 满足

bi+jmodT=sj,j=0,1,···,r−1

则称该状态是周期序列b位于第i位的r长状态,即考虑位置的r长状态可由该状态第一比特所处的位置和状态长度r确定.

例1序列=(00010111)周期为8,其中(000)的第一比特0是序列的第0位,且该状态是序列位于第0位的3长状态,(1000)是序列位于第7位的4长状态,(00)是序列位于第0位和第1位的2长状态.

定义 4对于复写序列=(b0b1···bT−1bT···bmT−1),称bi为序列的第i位,记为,并且当i≡jmodT时,有

其中,i=0,1,···,mT−1,j=0,1,···,T−1.

若r长状态 (s0s1···sr−1)满足

其中,i=0,1,···,T−1,j=0,1,···,r−1.则称该状态是序列位于第i位的r长状态.根据定义,给定一个r长状态,它在序列的位置与其在序列中的位置相同.

例2序列=(00010111)周期为 8,则=(000101110001011100010111),其中为序列的第22位,此时=1.(1000)是序列位于第7位的4长状态,(00)是序列位于第0位和第1位的2长状态.

定义5给定周期序列c=(c0c1···cT−1),r长状态 (ci+1ci+2···ci+r) 称为r长状态 (cici+1···ci+r−1)的后继,更进一步考虑n长状态及其位置,将位于第i位的n长状态记为ci=(cici+1···ci+n−1),即=(ci+1ci+2···ci+n) 是=(cici+1···ci+n−1) 的后继,i=0,1,···,T−1. 记不考虑位置时的n长状态.(这里所有下标取模T的最小非负整数)

定义7将周期序列循环右移一位的变换称为的循环右移变换,记为R.设=(a0a1···aT−1),则在循环右移变换R下的像为:

定义Ri为循环右移变换R的i次复合,即

特别地,R0=.

定义8对于两条周期序列和,若存在d∈N,使得=Rd,称和平移等价,记作;若不存在这样的d,则称和不平移等价,记作≁

2.2 de Bruijn序列及其变形

若一条序列的周期为2n,且2n个不同的n长状态在一个周期中出现且仅出现一次,则称该序列为n级de Bruijn序列.对于一条n级de Bruijn序列,“减变形”和“加变形”规定如下:

“减变形”:将de Bruijn序列中n长全0状态替换为n−1长全0状态,n长全1状态替换为n−1长全1状态,得到一条周期为2n−2的新序列,记为序列.

“加变形”:将de Bruijn序列中n长全0状态替换为n+1长全0状态,n长全1状态替换为n+1长全1状态,得到一条周期为2n+2的新序列,记为序列.

2.3 编织法及其性质

2.4 编织法构造de Bruijn序列

综上,利用编织法可实现由一条n级de Bruijn序列来构造四条 2n级de Bruijn序列.进一步地,迭代使用上述算法,即可实现由一条n级de Bruijn序列来快速构造四的方幂条更大级数的de Bruijn序列.

3 主要结果

由定义9知,编织序列和分别决定了映射f和g,因此其间的差异性可以由映射f和g的差异性来刻画,而映射f和g的差异性定义如下.

定义 10对于映射f和g,若存在x∈A,使得

f(x)=g(x)

则称映射f和g在x上无差异;若存在x∈A,使得

则称映射f和g在x上有差异.进一步地,令

引理 3设x=(e0e1···e2n−1)∈A,若 (e0e2···e2n−2)∈P{(1000···00),(0111···11)},则

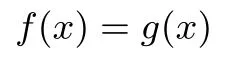
满足引理3条件的x有2n(2n−4)=22n−2n+2个,即至少有22n−2n+2个x使得f(x)=g(x).引理3中给出的条件是f(x)=g(x)成立的充分不必要条件,有引理4和引理5为证.

引理 4设x=(e0e1···e2n−1)∈A, 若 (e0e2···e2n−2)=(1000···00) 并且 (e1e3···e2n−1)=(0000···00)或 (1111···11),也即当x=(1000···00) 或x=(1101···01) 时,有

f(x)=g(x)

证明:当x= (1000···00) 时, 即 (e0e2···e2n−2)= (1000···00) 且 (e1e3···e2n−1)=(0000···00), 由于 (0000···00) 只能来源于序列, 因此 (1000···00) 来源于序列, 此时

f(x)=g(x)=e2n=1

当x=(1101···01) 时,即 (e0e2···e2n−2)=(1000···00) 且 (e1e3···e2n−1)=(1111···11),由于(1111···11)只能来源于序列,因此 (1000···00) 来源于序列,此时

f(x)=g(x)=e2n=1

综上,当x=(1000···00) 或x=(1101···01) 时,有f(x)=g(x).

同理可证明以下引理.

引理 5设x=(e0e1···e2n−1)∈A, 若 (e0e2···e2n−2)=(0111···11), 并且 (e1e3···e2n−1)=(0000···00)或 (1111···11),也即当x=(0010···10) 或x=(0111···11) 时,有

f(x)=g(x)

由引理3–5可知, 当x∈{(0010···10),(0111···11),(1000···00),(1101···01)}或 (e0e2···e2n−2)∈P{(1000···0),(0111···11)}时,有f(x)=g(x).此时,共有 22n−2n+2+4个x使得f(x)=g(x).以下讨论映射f和g出现差异的情况.

引理 6设x=(e0e1···e2n−1)∈A,若 (e0e2···e2n−2)=(1000···00) 且 (e1e3···e2n−1)∈P,则

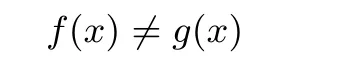
综上可得,当 (e0e2···e2n−2)=(1000···00) 时,

f(x)=1,g(x)=0

若 (e1e3···e2n−1)∈,有

f(x)=0,g(x)=1

综上可知,(e1e3···e2n−1)遍历了序列中所有的n长状态,也即集合P中所有元素,故当(e0e2···e2n−2)=(1000···00) 且 (e1e3···e2n−1)∈P,有f(x)(x).

由引理6可知,满足引理6条件的x有2n−2个,即有2n−2个x使得f(x)(x),同理可证如下引理.

引理 7设x=(e0e1···e2n−1)∈A,若 (e0e2···e2n−2)=(0111···11) 且 (e1e3···e2n−1)∈P,则

此时有2n−2个x使得f(x)(x).最后考虑仅在序列中出现的n长状态 (0000···00)和 (1111···11).

引理 8设x=(e0e1···e2n−1)∈A,若 (e0e2···e2n−2)=(0000···00),则

(2) 当 (0000···00) 为时,=(0000···00) 的后继为=(0000···01),同上讨论可得,

综上可得,当 (e0e2···e2n−2)=(0000···00) 时,

因此, 对于x=(e0e1···e2n−1)∈A, 当 (e0e2···e2n−2)=(0000···00) 时, 若 (e1e3···e2n−1)∈,有

f(x)=0,g(x)=1

f(x)=1,g(x)=0

综上可得,当 (e0e2···e2n−2)=(0000···00),有f(x)(x).

由引理8可知,满足引理8条件的x有2n−2个,即有2n−2个x使得f(x)(x).同理可知,当(e0e2···e2n−2)=(1111···11) 时,可得引理9.

引理 9设x=(e0e1···e2n−1)∈A,若 (e0e2···e2n−2)=(1111···11),则

此时有 2n−2个x使得f(x)̸=g(x).由引理6–9可知,共有 4(2n−2)=2n+2−8个x使得f(x)̸=g(x).再由引理3–5可知,有 22n−2n+2+4个x使得f(x)=g(x),而|A|=22n−4,映射f和g在 22n−2n+2+4个元素上无差异,在 2n+2−8个元素上有差异,由计数可知,引理3–5和引理6–9事实上给出了映射f和g出现差异的充要条件,整理得到定理1.

定理 1对于定义9中映射f和g,设x=(e0e1···e2n−1)∈A,f(x)(x)当且仅当满足下列情形之一:

(1)(e0e2···e2n−2)=(1000···00) 且 (e1e3···e2n−1)∈P;

(2)(e0e2···e2n−2)=(0111···11) 且 (e1e3···e2n−1)∈P;

(3)(e0e2···e2n−2)=(0000···00) 或 (1111···11).

表1 编织序列和的差异Table 1 Differences betweenand

表1 编织序列和的差异Table 1 Differences betweenand

注 1表中√ 表示有差异,×表示无差异

4长状态 I 1=In(b,a3) I 2=In(a3,b)有无差异(0001) 0 1 √(0010) 0 0 ×(0011) 1 0 √(0100) 1 0 √(0110) 0 1 √(0111) 0 0 ×(1000) 1 1 ×(1001) 1 0 √(1011) 0 1 √(1100) 0 1 √(1101) 1 1 ×(1110) 1 0 √

4 结束语

虽然利用编织法可以实现由较低级数de Bruijn序列构造高级数de Bruijn序列,但是需要考虑两个方面的问题.

一方面,由一条n级de Bruijn序列编织构造的两条编织序列,其差异率为

表2 n=2至6对应的差异率Table 2 Difference rates for some n

由表2可知,当n逐渐增大时,由编织法生成的两条编织序列的差异数虽然逐渐增长,但是差异数的增长速度远低于编织序列2n长状态个数的增长速度,导致差异率越来越低.当n→∞时,事实上,当n=12时,差异率为0.0009761,已经不足千分之一,也即通过编织法得到的两条编织序列的相似性超过了99.9%.因此,虽然利用编织法可构造出更高级数的de Bruijn序列,但这些de Bruijn序列相似性较高,这也表明从一条n级de Bruijn序列出发利用编织法构造的2n级de Bruijn序列,级数n与所得编织序列的差异率是一对矛盾,差异率随着级数n的增大而减少.

另一方面,注意到,多次利用编织法可从一条n级 de Bruijn序列出发快速地构造大量的更高级数 de Bruijn序列.例如,当n=2时,一次编织可以得到两条差异率为 0.667的编织序列,补足所缺片段得到四条 4级 de Bruijn序列,再以这些 4级 de Bruijn序列为基础序列,进一步编织并补足所缺片段可得到十六条 8级 de Bruijn序列,也即从一条 2级 de Bruijn序列出发,利用编织法两次可得到十六条 8级 de Bruijn序列,依次下去,可得到四的方幂条 de Bruijn序列,具体过程参见文献 [13].从一条n级 de Bruijn序列出发,经过一次编织所得到的编织序列的差异性 (组内差异),本文已研究清楚.在编织序列基础上补足所缺片段得到四条 2n级 de Bruijn序列,以差异性较大的两条2n级de Bruijn序列为基础序列,它们经过编织所得序列的差异性(组间差异),是下一步需要考虑的问题.