超声振动去毛刺工具头的设计及振动特性分析

袁野杰，魏周玲，傅波

（四川大学 机械工程学院，成都610065）

0 引 言

在现代制造领域中，大多数加工方法均不可避免使加工零件产生毛刺，这将影响零件的精度及后续的加工和装配，降低机械产品的整体性能，甚至会危及设备的安全运行[1]。因此，去毛刺是机械加工中一道不可缺少的工序。随着材料技术、精密机械等领域的不断发展，对加工零件中的深孔、盲孔、交叉孔等特殊位置毛刺的去除要求越来越高，加之节能环保的要求，研究新型去毛刺方法势在必行[2]。本文对超声振动去毛刺系统进行了研究，重点对工具头进行了设计和仿真优化，为超声振动去毛刺系统在生产中的应用打下基础。

1 超声振动去毛刺系统的组成结构

毛刺是工件加工后残留在工件母体上的一小部分材料，要去除它必须使去除毛刺的应力超过其极限应力。将定值或周期性外力作用于毛刺材料上，使其达到疲劳强度极限而失效或发生变形并超过临界断裂应变，毛刺即可去除。超声振动去毛刺时，去毛刺工具头在超声振动系统的驱动下周期性地碰撞毛刺，致使毛刺反复受力，当所受力超过了毛刺材料的屈服极限时，毛刺即被折断切除，从而达到去除毛刺的目的[3]。

本文研究的超声振动去毛刺系统主要由超声波发生器、换能器、变幅杆和去毛刺工具头组成，如图1所示。超声波发生器1输出的高频电信号经由换能器2转换成纵向机械振动，随后传递给变幅杆3进行振幅放大，最后将高频定振幅传输给去毛刺工具头4，工具头在超声振动驱动下对工件上的毛刺进行高速撞击，直至毛刺断裂去除，并使工件表面达到一定的平整度。该系统采用夹心式压电超声换能器，此类换能器容易制造，成本低廉，且机电能量转换效率高，性能稳定，在功率超声领域应用广泛[4-5]。

图1 超声振动去毛刺系统

2 超声振动去毛刺工具头的设计

工具头是超声振动去毛刺系统的重要组成元件，其振动模式对毛刺的去除质量有重要影响。该系统工具头采用了纵扭振动模式，将纵振和扭转振动复合在一起，以期实现对交叉孔等特殊位置毛刺的高效率去除。

为了实现纵扭振动，需要在工具头处将超声换能器的纵向振动转换为扭转振动。传统的将纵向振动转换为扭转振动的方法是利用2个换能器在变幅杆的两端进行作用，形成推挽式的扭转振动，可获得较大的输出功率，但转换效率不高。系统采用在传振杆上开出若干斜槽，使纵向振动在传振杆中传播时出现扭转分量，实现振动模式之间的转换，以获得较大输出功率和转换率的扭转振动[4]。系统去毛刺工具头结构如图2所示，工具头的刀柄由一段圆柱实体和一段筒壁开有斜槽的圆筒构成，斜槽将输入端传递的一部分纵向振动转换成扭转振动。工具头的初始尺寸按照谐振频率28 kHz，应用传输矩阵法计算得到[6]。

图2 纵扭复合振动工具头结构

3 超声振动去毛刺工具头振动特性分析及优化

为了验证所设计的工具头结构能否在28 kHz超声电源驱动下产生谐振，且振型与设计一致，借助于有限元分析软件ANSYS，对其振动特性进行分析和优化[7-8]。

3.1 工具头的模态分析

首先研究不同尺寸的矩形斜槽对工具头共振频率及振型的影响。在SolidWorks中建立纵扭复合振动工具头的参数化模型，其中斜槽长度a、宽度b、与工具头轴线的倾斜角r为参数变量，利用ANSYS Workbench软件的Design Xplorer模块对工具头进行多参数单一目标的有限元分析，获得各尺寸参数对共振频率的影响，如图3 所示。

图3 各尺寸参数对共振频率的影响

由图3中曲线变化可总结出：1）纵扭复合振动的共振频率随着斜槽与轴线夹角r的增大而在0°～10°范围内增大，在10°～20°范围几乎不变，在20°～90°范围呈下降趋势；2）斜槽长度a增大，会减小复合振动的共振频率；3）斜槽宽度b增大，复合振动的共振频率随之减小。

根据斜槽尺寸对纵扭复合振动共振频率影响的规律，对开有A～G型斜槽的纵扭复合振动工具头分别进行有限元模态分析，结果如表1所示。从表中数据可以证实此前总结出的斜槽长度a、宽度b、倾斜角r对共振频率的影响规律准确，还可总结出：1）增加斜槽行数，工具头输出的振幅和频率均有所降低；2）增加斜槽的列数，对共振频率和振幅的影响不大。

表1 几种斜槽类型的扭转振动工具头模态分析结果

图4 四种类型工具头的纵扭复合振动位移图

图4展示了A、B、E、F型斜槽工具头纵扭复合振动的位移云图。从图中可以看出，B型斜槽的工具头在产生纵-扭复合振动时，输出端的位移最大，但分布不均匀，而其共振频率27.845 kHz却很接近28 kHz，结合表1中的振动位移幅值大小，确定采用B型开槽工具头将纵向振动转换成纵-扭复合振动，但结构还需要进一步优化。

3.2 工具头的结构优化

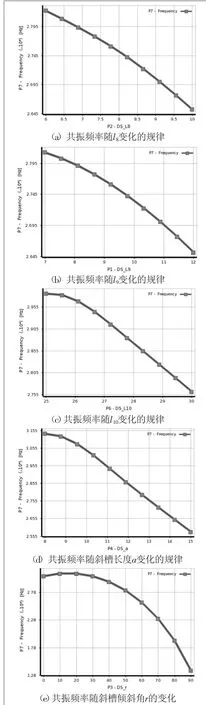
图5 各个参数变量对工具头共振频率的影响

由图2 可知，复合振动工具头的轴向尺寸受l8、l9、l10的影响，而斜槽长度a、宽度b和斜槽倾角r亦对共振频率的影响重大。根据制造加工能力，将斜槽的宽度b定为4 mm， 利 用ANSYS Workbench 软件的Design Xplorer模块对工具头进行多变量单目标的优化设计，得到27种变量组合，其中 l8、l9、l10、a、r单个参数变量对工具头共振频率的影响如图5所示。

从图中可以看出，工具头的复合共振频 率 随l8、l9、l10、a、r 的 增 大而逐渐减小。图6呈现了各变量因子对复合共振频率的影响敏感系数，可见工具头斜槽倾斜角r对共振频率的影响最为敏感，斜槽长度a的敏感性次之，据此建立主要影响因子r和a在设定范围内变化所得的共振频率响应三维图，如图7所示。

图6 各参数对共振频率的影响敏感系数

图7 l10和a参数的频率响应

根据优化分析后最终确定l8=10 mm，l9=10 mm，l10=28 mm，开槽长度a=10 mm，宽度b=4 mm，倾斜角r=35°。

根据改进后的工具头结构重新建立有限元分析模型，进行模态分析，得到工具头纵-扭复合振动的共振频率为28.361 kHz，振动位移云图如图8所示。从图中可以看出，振动位移最大分布在刀头端，且分布均匀，纵-扭复合振动的工具头设计合理。

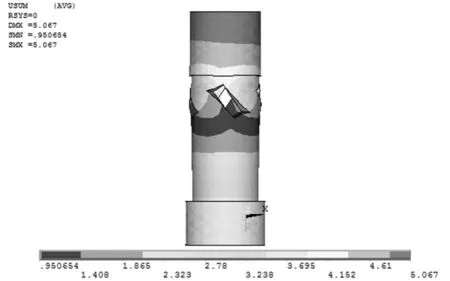
图8 优化后的B型斜槽工具头纵-扭复合振动位移云图

4 结语

介绍了一种超声振动去毛刺系统，分析了其组成结构。对纵扭超声振动去毛刺工具头的结构进行了设计分析，利用有限元分析软件ANSYS对具有不同斜槽类型的纵扭复合振动工具头的振动特性进行了模态分析，对工具头的结构进行了优化，设计了合适的超声振动去毛刺工具头结构，为超声振动去毛刺系统的进一步研究和生产应用打下了基础。