一种基于弦截法的预估校正格式
王 岩,何斯日古楞
(内蒙古大学 数学科学学院,呼和浩特 010021)
0 引言
科学和实际工程中的许多问题常常归结为求解非线性方程或(随机)微分方程问题[1-2].但是,绝大多数问题都难以用解析法求其精确解,只能用数值方法给出其近似解.因此,出现了插值法、函数逼近、Euler法、R-K法和迭代法等多种数值手段[1-4].近年来,针对方程求根问题已有多种迭代求根法[5-11].文献[5]给出了以拟牛顿迭代计算预估值,以steffensen迭代计算校正值的一种预估校正格式,证明了单根处的三阶收敛性.文献[6]根据文献[5]的预估校正格式和差商思想提出了3种五阶求根格式.文献[7]给出了一种至少三阶收敛的迭代公式.该方法虽避免了求函数的二阶导数,但仍需要求一阶导数.文献[8]引入动力系统,结合Euler方法构造了一种迭代格式,证明了其至少二阶收敛.基于“抛物线化-线性化”思想,文献[9]构造了与Muller法相同收敛阶的一种改进公式并分析了收敛性.基于弦截法,文献[10]构造了收敛阶为2.618的预估校正(简记为P.C.2)格式,并给出了数值算例.在此基础上,文献[11]利用文献[9]的思想,构造了收敛阶为5.236的预估校正(简记为P.C.3)格式.文献[11]所提格式虽然具有较高收敛阶,但每步迭代需要两次预估,计算四次函数值,计算步骤多.据了解,未见介于P.C.2 格式和P.C.3 格式之间的迭代格式.
为此,本文将弦截法与文献[9]的思想结合,构造了一种新的预估校正(P.C.)格式:


(1)
该格式的每步迭代只需一次预估,计算三次函数值.通过理论分析证明了本文所提格式的收敛阶为2.956 3,接近三阶,并通过数值算例验证了其可行性与有效性.
1 迭代公式的推导以及收敛分析
设x*是f(x)=0的精确根,利用弦截法得:
(2)
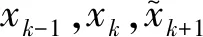
(3)
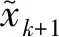
(4)

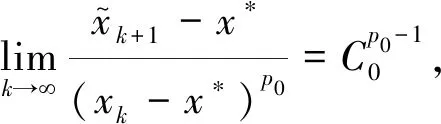
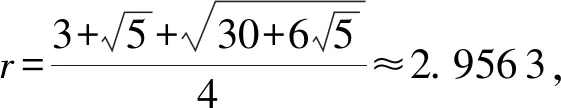
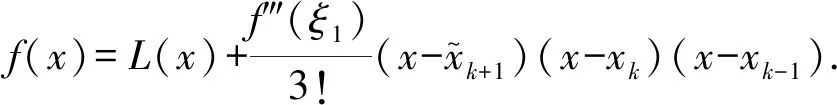

(5)

(6)
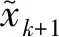
(7)


从而表明迭代过程(1)是超线性收敛.
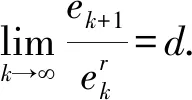
进一步,略去式(7)的高阶无穷小,有:
(8)
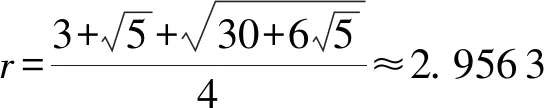
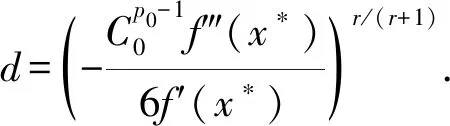

表1 迭代法计算结果Tab.1 Computing results forIterative methods
2 数值试验
为验证本文所提迭代格式(1)的可行性和有效性,对非线性方程:
f1(x)=xex2-sin2x+3cosx+5=0
用Matlab软件进行了数值实验,与文献[10]的迭代格式(P.C.2)和文献[11]的迭代格式(P.C.3)进行了比较.本文所给格式需要两个初始值x-1,x0,其中初始值x-1=x0-2×10-6,计算过程采取双精度,停止准则采用|xk-xk-1|<10-6,计算结果如表1所示.