圆管中聚合物减阻剂的减阻机理研究与评价

樊 帆，周福建，刘致屿，杨 钊

（中国石油大学（北京）非常规天然气研究院，北京102249）

近年来，随着致密油藏的大规模开发，超深水平井数量不断增加，压裂规模也不断扩大。水力压裂过程中，滑溜水的减阻性能是影响低渗透地层压裂的重要因素之一，因此越来越受到重视[1]。将滑溜水用于压裂复杂缝网，不仅使初始产量最大化，还可减少水力压裂过程中的摩阻损失，提高泵送速率，减小泵的尺寸[2]。

滑溜水是一种水基压裂液，其主要成分为聚丙烯酰胺、聚环氧乙烷、瓜尔胶及其衍生物等长链聚合物。研究发现，将低质量分苏的聚合物/纤维添加到流体中，可显著降低摩阻[3]。这种现象对于减少流体中的能量消耗、增加流速和减小泵的尺寸等意义重大[9]，但是却很难进行准确的模拟来预测减阻剂的减阻率（DR）。在过去的40多年，一些学者已经进行了多领域的实验和数值模拟研究聚合物减阻机理，但是由于受聚合物浓度、温度、盐度和管道粗糙度等多重因素的影响，其确切的减阻机制仍然尚不明确[4-12]。通常用于描述减阻剂均匀分布模式下的减阻机理分为三类：第一类以边界层理论为代表，认为减阻作用是减阻剂改变流体宏观流动状态；第二类是以湍流抑制理论为代表，认为减阻机理在于改变湍流结构，减少湍流能量消耗；第三类则认为减阻剂具有弹性，其微观结构在流动时发生变化从而减阻，以黏弹性理论为代表。但以上机理均是以减阻剂具有时均性为前提，三种情况均没有考虑流动过程中减阻剂的结构变化。

本文基于减阻剂在流动过程中微观结构的动态变化前提下，提出了一种用于计算湍流管道中聚丙烯酰胺四元共聚物添加剂（DR800）减阻效果的简化建模方法。其主要思路是以应力平衡方程为基础，建立模型来解释黏性剪切应力、雷诺剪切应力和黏弹性剪切应力等对摩阻系数的贡献。该模型在一定程度上解释了减阻率如何随DR800质量分数以及流速变化而变化，这与聚合物溶液的构象张量有很大关系。针对此模型对室内环路测试实验进行验证，以准确测量不同质量分数下的减阻率，其结果与模拟结果一致。在实验中设置可视化窗口用于观察流动过程中微观结构变化。通过对比数值模拟和实验结果，得出减阻剂结构变化时的减阻机理。同时，此模型需进一步修正相关参数，以便更好地应用于现场。

1 模型建立与数值模拟

图1为管流几何模型。如图1所示，选取一段长度为L，半径为R的圆管计算区域，在圆柱坐标系下，z轴为流体流动方向。

首先测量聚合物溶液的表观黏度和拉伸黏度，将其作为Giesekus模型参数，通过应用Giesekus本构方程，建立表面活性剂溶液运动控制方程（1）-（3）：

连续性方程：

动量方程：

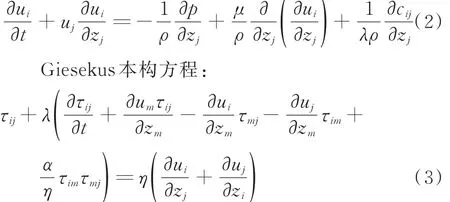
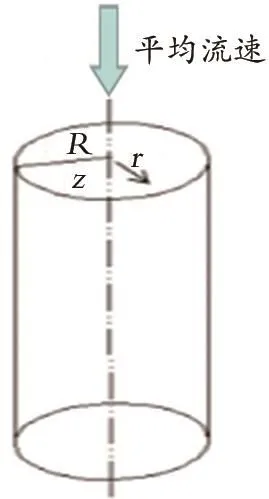
图1 管流几何模型Fig.1 Tube flow geometry model

其中，λ和α分别为弛豫时间和迁移因子;η为添加剂的零剪切黏度；μ为动力黏度。以管道半径R为特征长度，摩擦速度Uτ为特征速度，引入以下无量纲变量：

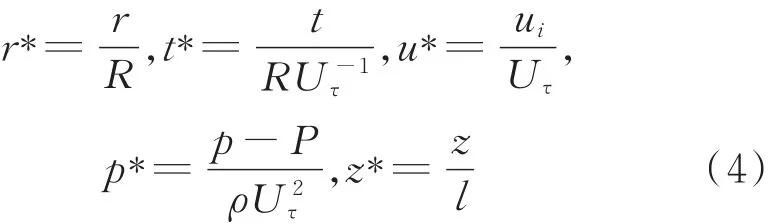
定义主雷诺数为：

局部摩阻系数定义为：

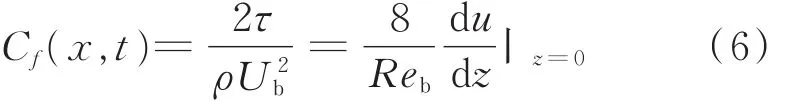
以定义的无量纲量和平均算子为基础，建立z轴上不可压缩管流平均雷诺数纳维-斯托克雷诺兹方程：

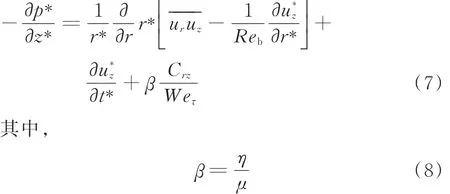
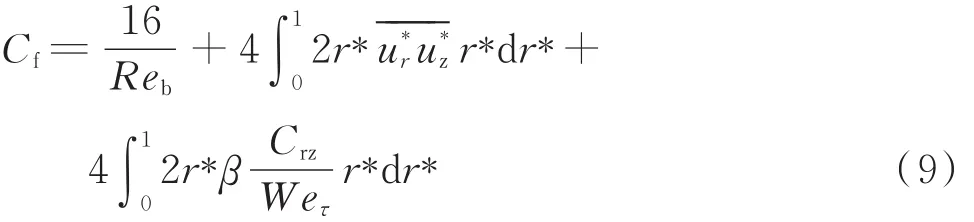
方程（9）可以计算出黏性剪切应力、雷诺剪切应力和黏弹性剪切应力对摩阻系数的贡献。该方法首先由K.Fukagata等[3]提出用于评价主动湍流控制，在本文中被延伸作为滑溜水圆管湍流摩阻预测公式。摩擦系数的第一项是黏性贡献，仅与平均雷诺数相关，即在相同流动条件下，滑溜水与牛顿流体的黏性贡献相同。第二项为湍流贡献，与雷诺剪切应力的加权平均值成正比，加权表明雷诺应力对不同位置的湍流有不同的贡献。越靠近壁面，对摩擦系数贡献越大;第三项为黏弹性贡献，该项为牛顿流体和聚合物溶液之间的主要差异，其中Crz（构象张量）表征聚合物添加剂的微观状态。从物理学的角度来看，可以将其视为描述分子变形程度的物理量。研究表明，构象张量可以通过方程（10）计算[5]：

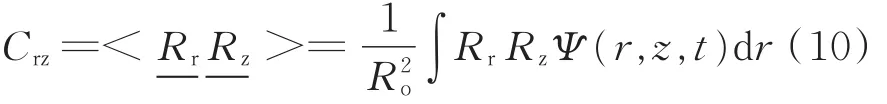
其中，Rr、Rz用于表示大分子链末端矢量，R2o是大分子的均方旋转半径，对于主要成分是二丙烯酰胺二甲基丙烷磺酸的DR800来说，R2o=0.23×10-7m。Ψ(r，z，t)是大分子构型空间分布函数，方程（10）用二阶张量可以很好地描述高分子在三维空间内的取向，从而将空间构象问题转化为一个空间内的取向问题[5]。由于Ψ(r，z，t)随大分子位置和流动时间而变化，很难知道各流速和质量分数下的分布函数。因此可以简化计算：二阶高分子取向张量是对称的，它具有三个正交特征向量a1、a2、a3。特征值表示沿相应特征向量方向上的高分子数量。

以0.07%DR800为例，显微电镜下溶液中的大分子聚合物近似网格均匀分布，聚合物分子均匀分布在三个主轴上，如式（11）所示（见图2（a））。对于0.01%DR800、0.03%DR800分别如式（12）、（13）所示（见图 2（b）、（c））。

图2 聚合物添加剂的TEM图像Fig.2 TEM image of polymer additive

通过这种方式，可以近似计算不同质量分数0.01%、0.03%、0.07%、0.10%的随机分布函数。但对于其他质量分数，大分子微观结构没有明显的特征。为避免无意义的振荡压力场，计算网格选取交错网格，将无量纲压力P*置于网格中心，速度分量置于网格周围，计算域大小为πR2×10R的网格数为90×88。采用Adams-Bashforth格式离散控制方程。定义减阻率为：

式中，Cfo为清水的摩阻系数；Cf为添加了DR800的滑溜水的摩阻系数，即可得到图3、4。

2 实验设备

2.1 设备组成

为验证数值模拟结果，建立了室内摩阻环路测试系统，如图5所示。

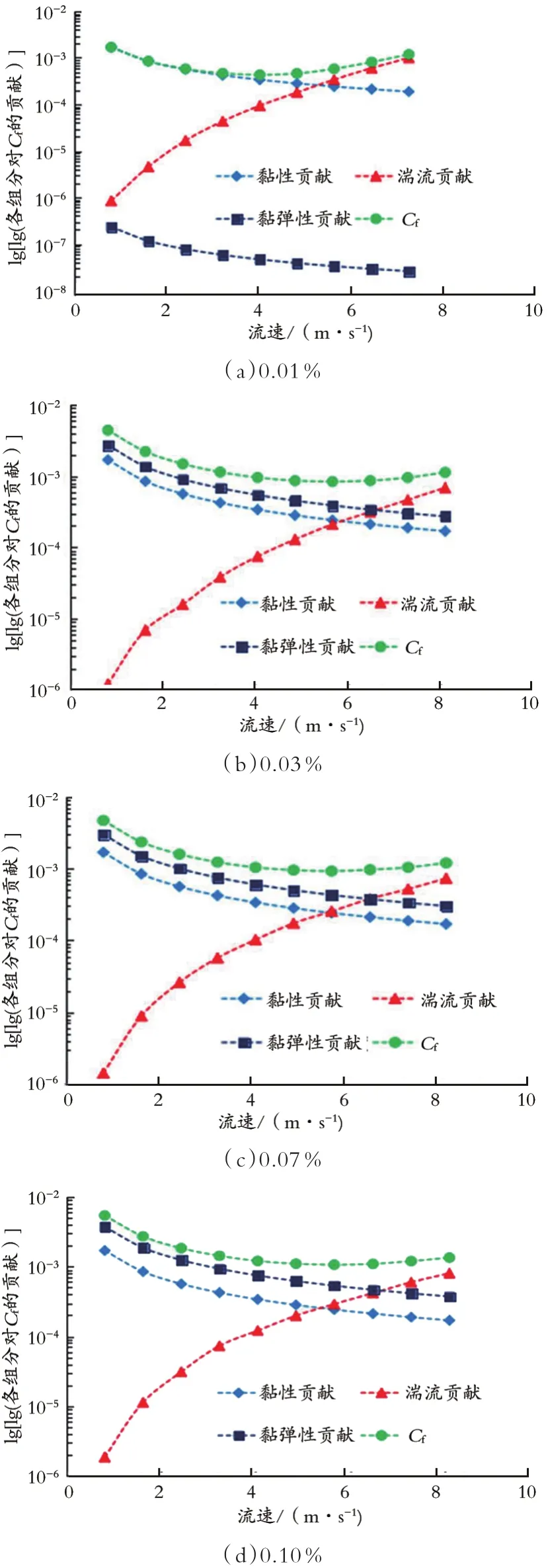
图3 不同速度下各组分对Cf的贡献Fig.3 Contribution to Cfof each component pair at different speeds

为了更好地模拟现场条件，采用大容量螺杆泵，其最大泵送速率为2.5 m3/h；顶部带有氮气气囊的中间蓄能器作为流动稳定器，用于消除来自泵的流体的脉冲能量，从而使环路中的流体快速达到平衡；三根长度均为3 m、内径分别为6、8、10 mm的不锈钢管道；为了使管道拐角处的附加剪切效应最小化[7]，在距离拐角两端0.25 m处设置压力传感器测量压降。由于流动管道存在尺度效应，直径可以显著地影响流体的流动行为，因此在测试前先校准三个管内径精确值。为了精确控制流体的流速，使用质量流量计监测回路中的流量，同时向螺杆泵提供反馈以进行微调。此外，在管道中设置一段有机玻璃管作为可视化窗口用来直观观测流态。

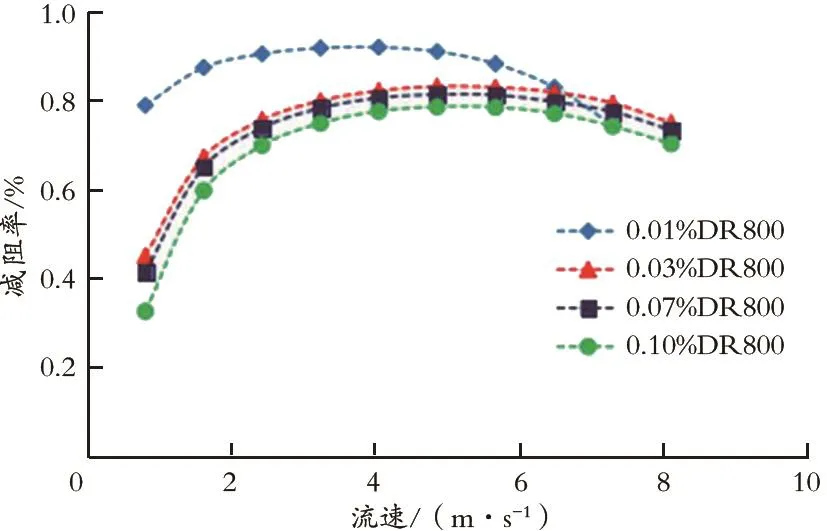
图4 不同质量分数的DR800减阻率Fig.4 Different concentrations of DR800 drag reduction rate

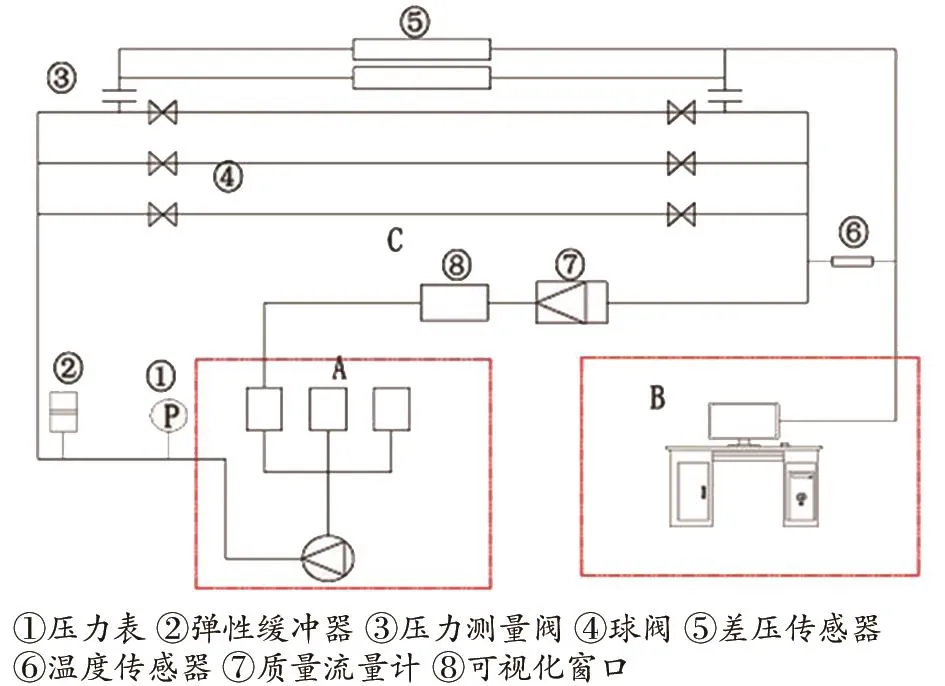
图5 室内摩阻环路测试系统平台Fig.5 Schematic diagram of indoor friction loop test system platform

2.2 设备校准

应用Prandtl-Karman相关方法校准三管的精确内径。为了校准管的内径，首先用淡水进行摩阻环路测试.具体方法如下：预先测量清水密度和黏度。然后在一定泵排量下测量压降。最后调整内径以匹配达西摩阻系数λ和Re，直至与Prandtl-Karman公式预测一致。得到结果，6 mm直径的管有效内径为5.86 mm；8 mm直径的管有效内径为7.59 mm；10 mm直径的管有效内径为10.46 mm[2]。图6为管道校准结果，由图6可知，实验数据点在基准线附近均匀分布，表明实验管道具有高精度，实验数据具有可靠性。

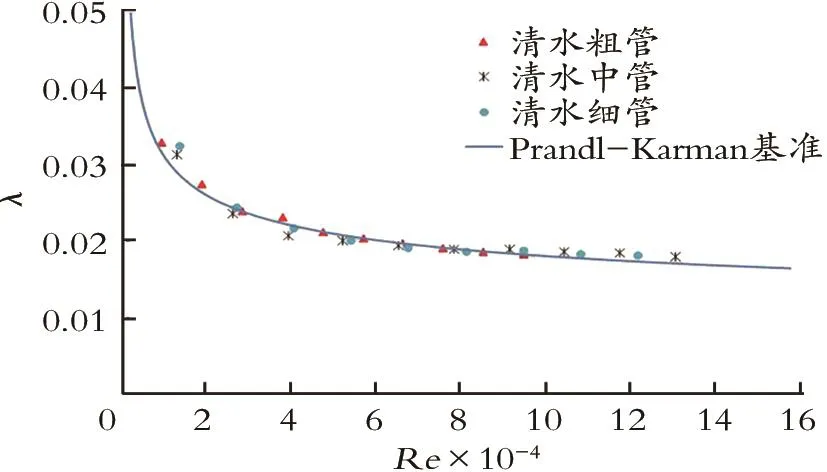
图6 管道校准Fig.6 Pipeline calibration results

3 数值模拟与实验测试结果

基于室内摩阻环路测试系统，在各流速下进行大量重复实验使误差最小化。

图7为数值模拟与实验测试的结果比较。基于不同质量分数下室内实验和数值结果比较，可以看出，此模型在减阻剂质量分数较高时比较准确。在高流速下数值结果显示出下降趋势，与实际结果不符。这可能是忽略温度对黏度的影响的结果。

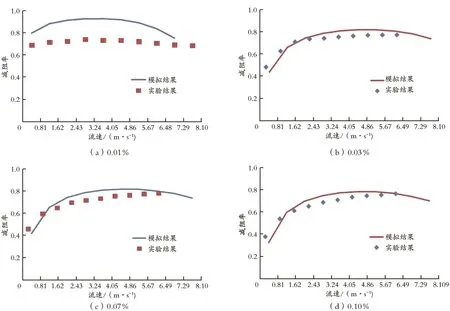
图7 数值模拟与实验测试结果比较Fig.7 Comparison of numerical simulation and test results

4 现场应用

选择lin No.18井进行摩阻试验。井结构为：上部158根76 mm的油管，长度为1 525 m；下部126根62 mm的油管，长度为1 212 m。现场测试的聚合物质量分数为0.08%。测量结果通过放置在井口和井底的压力计获得，如表1所示[6]。

将位移转换为速度用于比较现场测量结果与滑溜水模型模拟结果，图8为对比结果。由图8可知，DR800的减阻性能可以在一定范围内预测。数值模型中减阻率下降，且与实际存在一定的偏差，主要是由于地层温度对减阻剂黏度的影响在实验中没有考虑。

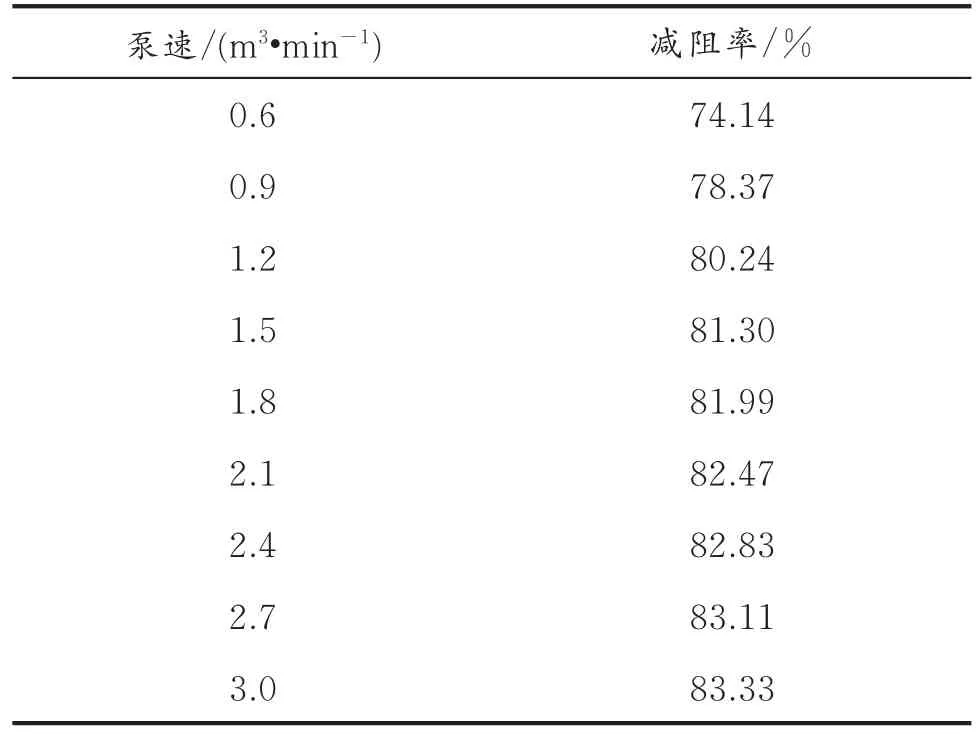
表1 滑溜水的现场测量Table 1 Field measurements of slick water

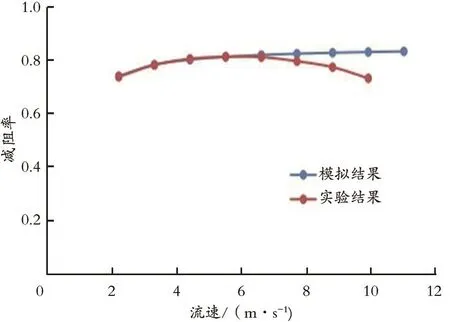
图8 实验结果与模型结果的比较Fig.8 Comparison of measurement results and model prediction

5 结 论

（1）随着流动的复杂性增加，黏性贡献和黏弹性贡献减小而湍流贡献增加。

（2）低雷诺数下，黏弹性剪切应力对摩擦系数贡献最大，而湍流可忽略不计。

（3）高雷诺数下，湍流的贡献迅速增加，为总贡献的主导部分，其次是黏弹性，黏性剪切应力最小。

（4）高速环境下，大分子链可能受到泵的剪切损伤，因此减阻率变小。

（5）高速下，数值结果显示出下降趋势，与实际存在一定的偏差，主要是由于地层温度对减阻剂黏度的影响未知引起。