让数学课堂弥漫着学生思维的张力
江梅

[摘要]苏教版小学数学教学打破了传统教材编排体系,将“繁、杂、旧、难”的独立成章的应用题删减,从三年级起纳入了专门讲解如何解决问题的策略。本文以此为研究对象,从“创设情境、领悟策略”入手,将让学生“动手操作、捕捉生成、灵活应用”作为教学手段,以求达到“体验策略、深化策略、优化策略、提升策略”的教学实效。本文结论:小学数学解决问题策略的传授,要合理运用情境教学法,多媒体辅助教学法,学生自主探探究、小组合作教学法等多元教学手段,让数学课堂弥漫着学生思维的张力。
[关键词]小学数学;解决问题;学生成长;策略;研究
一、比较——领悟策略
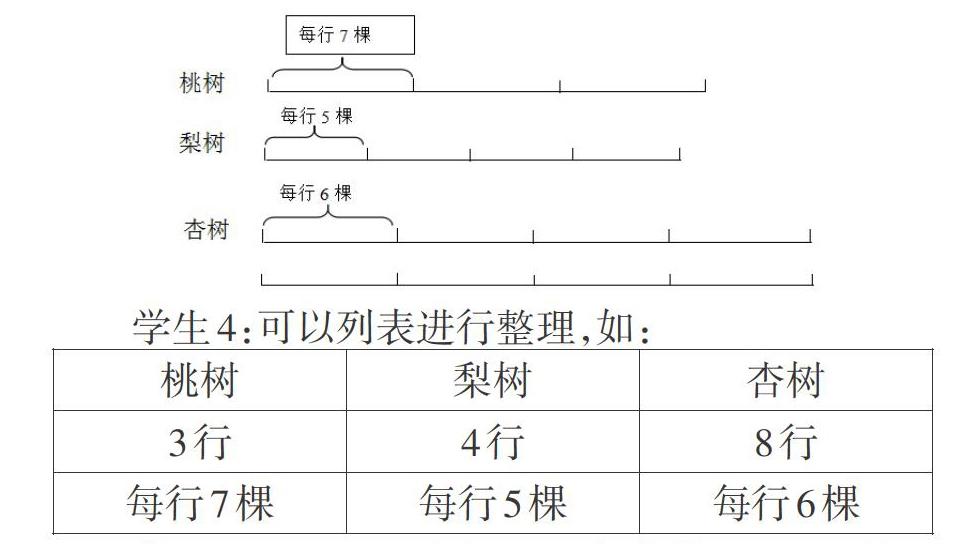
问题是数学的心脏,它贯穿于学习的全过程。“打开科学的大门就是问号。”设计富有思考价值的、优质的问题是有效课堂的前提条件。在教学过程中,善于创设探究性的问题,为学生探索问题、解决问题、发展思维导航。我在教授苏教版四年级《列表解决问题的策略》时,出示情境图:果园里栽了3行桃树,4行梨树,8行杏树,桃树每行7棵,梨树每行5棵,杏树每行6棵。你通过情境图观察,有何建议需要告诉大家?
学生1:只告诉我们已知条件没有问题,不是一道完整的应用题。
学生2:根据现有的条件,可以提不同问题。
学生:3:可以画图,更直观,如:
学生画线段图、列表、摘录条件信息整理,教师适时引导学生比较,从中了解列表整理信息的优势,掌握列表整理信息的方法,学会利用表格分析数量关系,形成解决问题的策略。这样通过探究性问题引发知识冲突,激发学生的求知欲,促使学生进行深刻的思考,学生在思考中解决了问题,掌握了新知识,激发了学习兴趣。
二、内化——体验策略
瑞士教育心理学家皮亚杰认为:“知识来源于动作。”一语道出了动手操作是小学数学课堂教学最直接的办法,动手是参与实践活动的开始。单纯地依赖模仿与记忆的数学课堂是无效课堂,动手实践,自主探索与合作交流是学生学习数学的重要方式。学生只有在亲历动手操作或体验才能做在其中,乐在其中,得在其中。例如:苏教版四年级数学《一一列举策略》一课,王大叔用18根1米长的栅栏围一个长方形的羊圈,有几种不同的围法?面积最大的是多少?学生带着疑问走进探索的活动中,通过动手实践,发现规律:有的围长6米,宽3米;有的围长7米,宽2米;有的围长5米,宽4米;还有的围长8米,宽l米。有这么多种,到底怎样围才能找到解决问题的方法呢?学生带着思考再次进行探究。终于发现18米其实就是长方形的周长,只要长和宽的和能等于9米就是正确的围法,而且按顺序进行列举做到不重复、不遗漏。在同学们的共同努力下,通过观察操作、计算等不同的方法,发现了有四种不同的围法,而且长和宽越接近的时候面积越大。当学生欲思而不通、欲达而不能时,通过亲自动手操作,始终把过程和结果紧密联系在一起,这样的探索饱含着发现的惊喜,闪烁着理性的光辉,带给学生成功的体验,同时了促进学生思维的发展。
三、生成——深化策略
数学课堂时时刻刻在向未知领域前行,随时都有可能发现彩虹和美丽的图景,而不是一切都必须遵循固有的路线前行而成为“萝卜干”。在追求课堂生成的背景下,只要我们正视和善待课堂上发现的错误现象,捕捉和利用其所蕴含的有价值的资源,就有可能成为开启学生智慧之门的钥匙,生长出比知识更具有魅力的因素,让数学学习在生成探究中走向深化。例如:在教逆向推想策略后,课后有一道练习:小军收集了一些画片,他拿出画片的一半多1张送给小明,自己还剩25张。小军原来有多少张画片?我先让学生尝试练习,结果几乎所有的答案都是小军原来有51张画片。学生说一般就是除以2,逆向就是乘2,多1张再加1张,算式是25×2+1,到底对不对呢?我适时引导让学生算出51张画片的一半是多少,学生因困惑而产生疑问,发现不对了,画片不可能是半张。这时学生意识到答案是错误的。于是开始重新寻找答案。学生纷纷喊道应该是52张。为什么?可以结合学过的画图法来分析其中的数量关系。学生们通过充分讨论,豁然开朗。
数形结合让学生的思维打开智慧之窗。这时我趁热打铁出了一道变式题把“多”字改成“少”字,学生很快就根据画图分析列出了算式(25-1)×2=48。由此可见,教师要善于捕捉学生在课堂情境中的每一次稍纵即逝的教育契机,并加以引导点拨放大,把它们转化成适于学生探索的一个个有探索价值的问题,那么每一个课堂意外都会演绎出异样的精彩。
四、延迟——优化策略
华国栋先生在《差异教学论》中告诉我们,学生个体的问题是存在差异性的,延时留空给学生以充分表达意见的机会,给大部分学生留有思考的时间与探索的空间,让他们在民主和谐的氛围中交流想法。教师应蹲下身来看孩子,了解他们的所思所想,保护思维的积极性和创造性,让更多的创意与灵感在等待中得以激发。
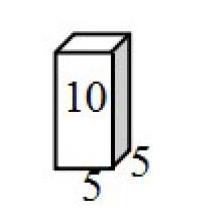
例如在计算上图所示图形的表面积时,所有学生都能用已学的知识解决问题,列式为(5x5+5x10+10x5)×2或5x10x4+5x5x2,正当教师想进入后续环节时,一个学生提出了“看上去明显有误”的算法5×5x10,在平静如水的课堂中,这个算法却似春雷,当这个声音响起时,所有学生都认为该生审题不清,大喊错了错了,算的是表面积不是体积,这时教师没有急于评价,真相究竟如何?
教师给学生提供充分说理的机会,他是这样解释的:长方体的底面积是5x5,上下底面积是5x5~2,侧面积是5x10,10是5的2倍,因此侧面积可算成5×5x2,四个侧面积是5x5x8,两个底面积是5x5x2,四个侧面再加上两个底面,不就是5x5x10吗?原来如此,5×5×10是他根据图形的数据特点利用侧面积与底面积不同的2倍关系,而灵机一动的便捷算法,这个算法看似求体积,实际是别出心裁地求表面积,其中蕴含的创新思考让人赞叹。对一个问题有差异性的见解时,教师应采用延迟性评价,留给学生更多的思考时间与空间,将学生的思维成因进行充分展示,让新思想在展示中不断进行有效碰撞,从而提高学生的思维能力,培养创新能力。
五、探索——提升策略
一節数学课赋予学生的绝不是一种单纯的数学知识,而是在为学生提供丰富的学习材料的同时,也为学生提供了一个广阔的思维空间。著名科学家达尔文也说过:世界上最有价值的知识是关于方法的认识。学习了画图策略后,出示这样一道题:一个正方形纸片的边长是20厘米,如果在这个正方形纸上剪去一个长是5厘米,宽是3厘米的小长方形后,剩余部分的周长是多少厘米?学生思考后展示。
学生1:这样剪去一个长方形(图1),通过观察示意图,我发现剩下部分的周长就是原来正方形的周长,即20x4=80(厘米)。
教师:想一想,还有不同的解法吗?
学生2:我是这样画图的(图2),通过观察示意图,我发现剩下部分的周长比原来正方形的周长多了两条小长方形的宽,剩余部分的周长是20x4+3x2=86(厘米)。

