轴承早期故障特征提取方法研究

张猛， 苗长云， 孟德军

(天津工业大学 电子与信息工程学院，天津 300380)

0 引言

滚动轴承是旋转机械的关键部件，也是最易发生故障的部件，一旦发生故障将对旋转机械造成损坏，甚至影响旋转机械的正常运行。滚动轴承的早期故障信号常以微弱信号形式存在，其特征提取是轴承故障诊断的难点[1-4]。传统包络解调算法的关键是从频率混杂的原始信号中将高频调制的故障信号解调出来，算法实现简便且准确率较高。袁杰[5]将包络解调算法应用到柴油机故障检测中，但无法有效解决滤波器参数选择问题。刘文朋等[6]将经验模态分解(Empirical Mode Decomposition，EMD)和谱峭度法相结合进行故障诊断，提高了信噪比，优化了带通滤波器参数，但是EMD自身产生的模态混叠现象会影响故障诊断结果。上述故障诊断方法自适应强、简单易用，但当原始信号掺杂非平稳噪声时，产生的虚假分量会使特征频率淹没在背景噪声中[7-8]。为此，本文使用快速谱峭度法设置滤波参数，将小波包分解和互补集合经验模态分解(Complementary Ensemble Empirical Mode Decomposition，CEEMD)相结合进行滚动轴承早期故障特征提取。快速谱峭度法能够筛选出含有滚动轴承故障特征的有用信息，并清晰地指出瞬态分量所在的频段，为带通滤波器的参数设计提供理论根据。小波包分解可在全频段对信号进行多层次的频带分解。CEEMD一方面能够解决模态混叠问题，另一方面也能有效减小白噪声残留带来的重构误差影响。

1 轴承早期故障诊断基本原理

1.1 谱峭度分析

谱峭度是一种用来检测信号中是否有非高斯成分的频域统计指标。通过计算信号频谱中各谱线对应的时域数据的峭度大小，可判定信号中的瞬态冲击成分具体属于哪些谱线，进而计算非高斯成分的频率分布范围[9]。

随机非平稳信号x(t)的Wold-Cramer分解形式为

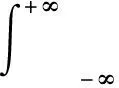
(1)

式中：Y(t)为频率f处的复包络；H(t,f)为t时刻冲击响应h(t,f)(系统传递函数)的频域表示。

Y(t)的四阶谱累积量定义为

(2)

式中S4Y(f),S2Y(f)分别为Y(t)的4阶和2阶瞬时矩。

Y(t)的2n(n为整数)阶瞬时矩S2nY(t,f)定义为

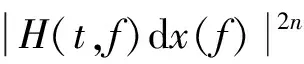
(3)

式中E为期望值。

信号Y(t)的谱峭度KY(f)定义为

(4)

由文献[10]可知，谱峭度是关于中心频率和带宽的函数。当带宽无限小时，谱峭度为0；当带宽过大时，谱峭度无法反映频带范围中的瞬态冲击现象。确定谱峭度值最大的频带的中心频率和带宽后，计算整个频域的谱峭度值，以确定包含瞬态冲击成分的信号x(t)及其所在的频率范围，从而寻找其中隐藏的瞬态信号。

1.2 小波包分解原理

小波包分解[11-12]能根据信号自身特性自适应地选取与信号频谱相匹配的频段，是一种比小波分解更为细致的分解方法。小波包分解对信号的分解、重构更加精细，可在全频段对信号进行多层次频带分解。频域空间和时域空间被越分越细[7]，能更好地对信号进行频带分离，减少其他频率成分干扰。

1.3 CEEMD方法

CEEMD是在EMD和集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)基础上提出的一种优化算法[13]。为克服EMD和EEMD算法缺陷，CEEMD方法向原始信号中添加正负成对的白噪声，然后对加噪信号实施EMD分解。CEEMD方法噪声添加次数较少，提高了计算效率[14]。

2 轴承早期故障特征提取流程

基于小波包分解和CEEMD的轴承早期故障特征提取流程如图1所示。

(1)利用Matlab软件对采集到的振动信号s进行快速谱峭度分析。正常轴承振动信号峭度值在3附近，偏离3的程度越大，轴承发生故障的概率越大。根据峭度最大化原则确定带通滤波器的中心频率和带宽，设计带通滤波器。

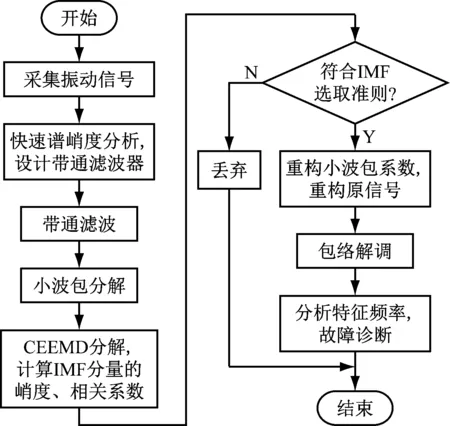
图1 基于小波包分解和CEEMD的轴承早期故障特征提取流程

(2)对原信号s进行带通滤波后，再进行1层小波包分解，得到低频信号s1和高频信号s2。

(3)分别对小波包分解信号s1,s2进行CEEMD分解，分解成2组若干个本征模态函数(Intrinsic Mode Function，IMF)分量。

(4)分别计算2组IMF分量的峭度值、相关系数。

(5)综合峭度、相关系数，选取最能反映轴承故障特征的IMF分量c1m,c2n，并以此作为重构小波包系数。

(6)根据重构小波包系数得到重构小波包信号C，对重构信号做包络解调分析，然后用快速傅里叶变换求出包络谱。

(7)根据包络谱分析结果提取滚动轴承早期故障信息。

3 仿真分析

3.1 轴承早期故障特征频率

将基于小波包分解和CEEMD的轴承早期故障特征提取方法应用于实际故障轴承数据。数据来自于美国西储大学实验平台。所用轴承为SKF6205-2RS深沟球轴承，其基本参数见表1。

表1 轴承参数

常见的轴承故障可分为外圈故障、内圈故障和滚动体故障。

内圈故障频率计算公式：

(5)

式中：n为转速；Z为滚珠个数；d为滚动体直径；D为轴承节径；α为接触角。

外圈故障频率计算公式：

(6)

滚珠缺陷故障频率计算公式：

(7)

计算得到该轴承故障特征频率，见表2。

表2 轴承故障特征频率

3.2 轴承内圈故障信号分析

内圈故障振动信号的时域波形如图2所示，可以看出时域图中出现明显的周期性冲击成分，对比正常轴承信号，虽有明显不同，但只能判断轴承是否存在缺陷，无法得知轴承缺陷所在位置。

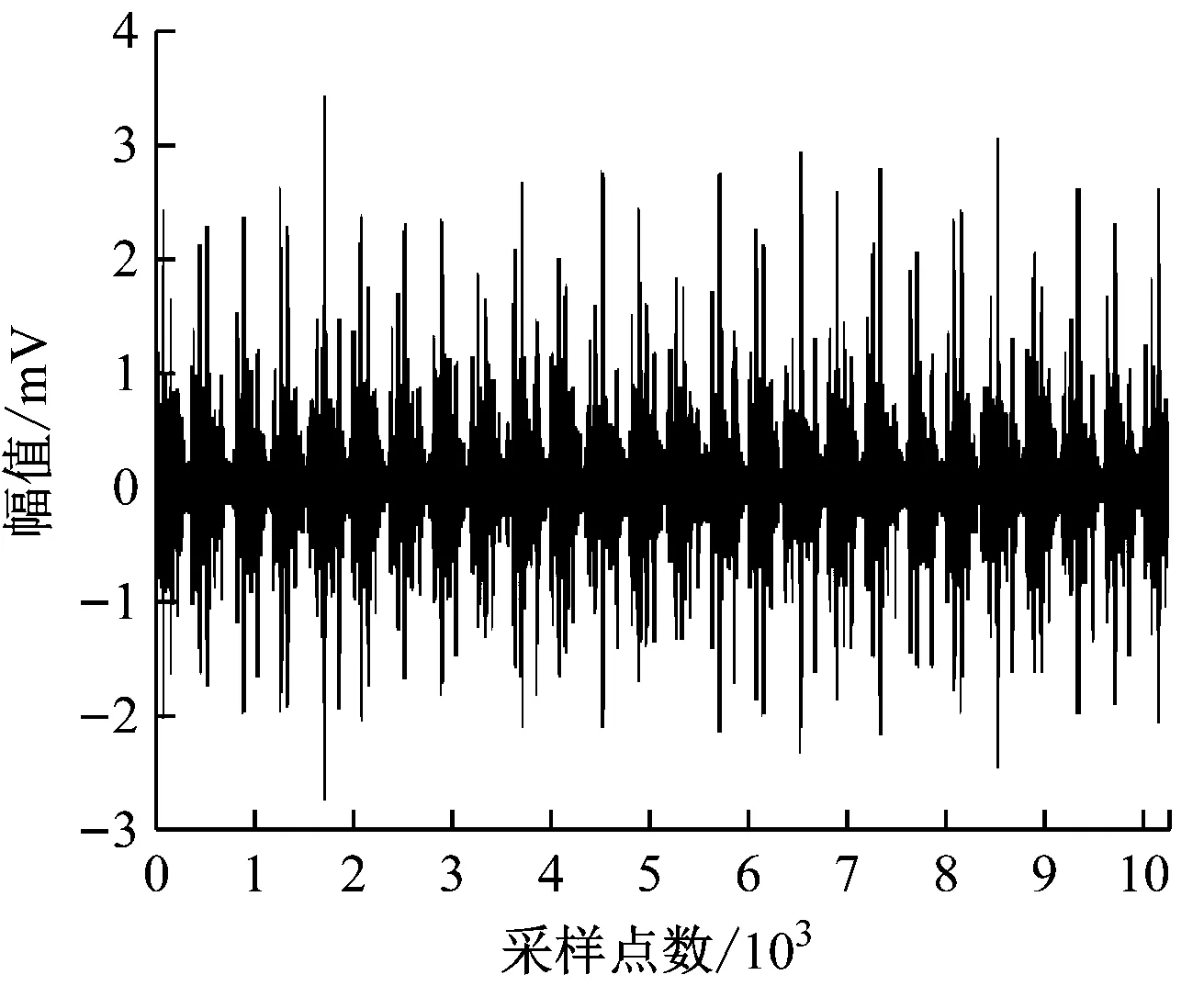
图2 内圈故障振动信号时域波形

3.2.1 谱峭度分析

内圈故障信号谱峭度如图3所示。将信号峭度值划分成7个level，以缩小区间范围，计算最大峭度值。从图3可看出，信号中心频率fc为4 125 Hz，带宽Bw为750 Hz，即频率在[3 375 Hz，4 875 Hz]范围内的峭度值最大。峭度值越大，即偏离正常值3的程度越大，故障概率也就越大。因此，选择该频段对故障信号进行带通滤波，滤波后的频域信号如图4所示，结合时域图可以看出滤波后的信号具有良好的降噪效果。

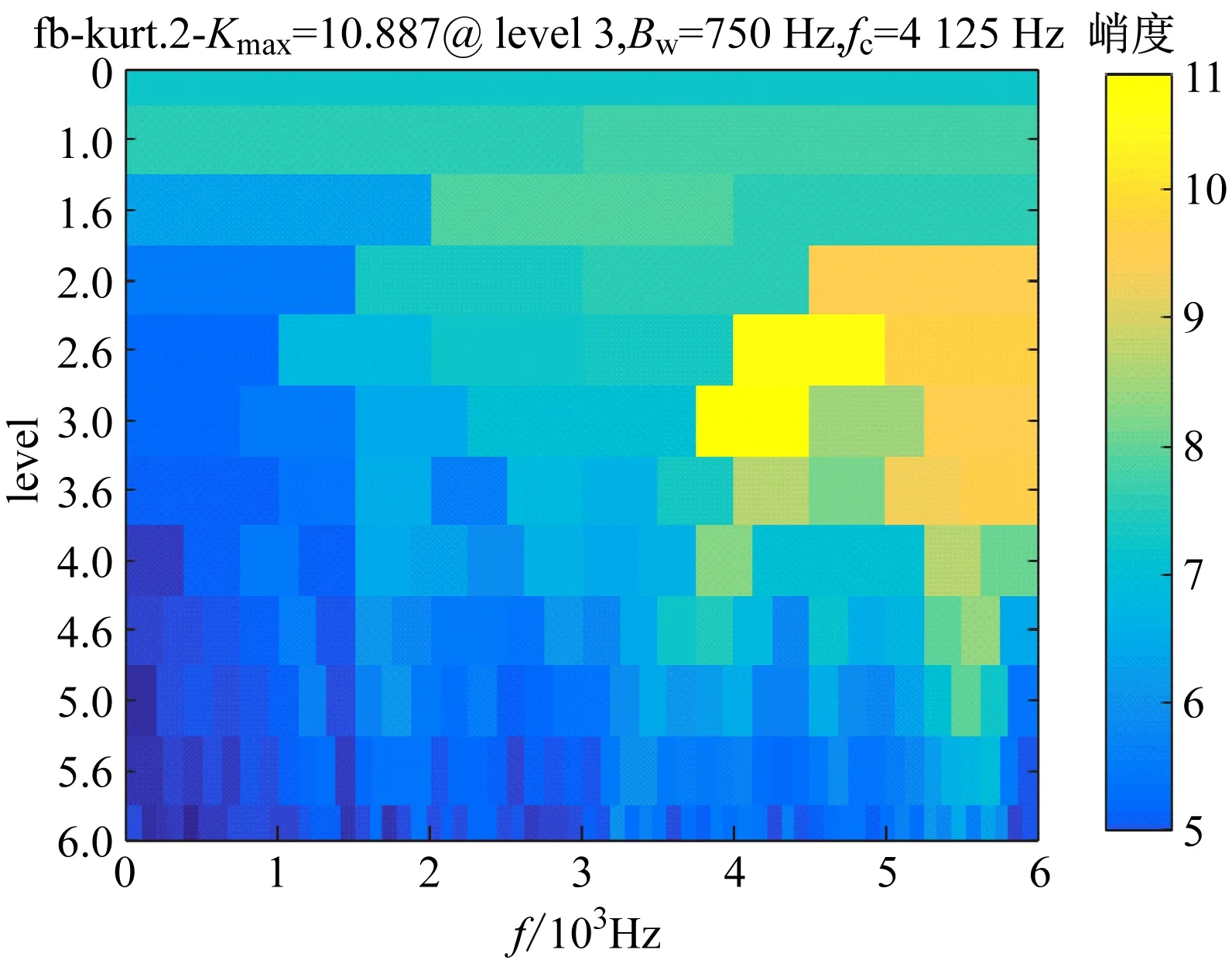
图3 内圈故障信号谱峭度

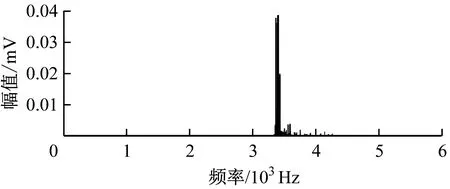
(b)滤波后

3.2.2 信号分解

选择db5小波基对轴承故障信号实行1层小波包分解，分解结果包含低频近似信号s1和高频细节信号s2两个部分。分别对信号s1，s2进行CEEMD分解，如图5、图6所示。

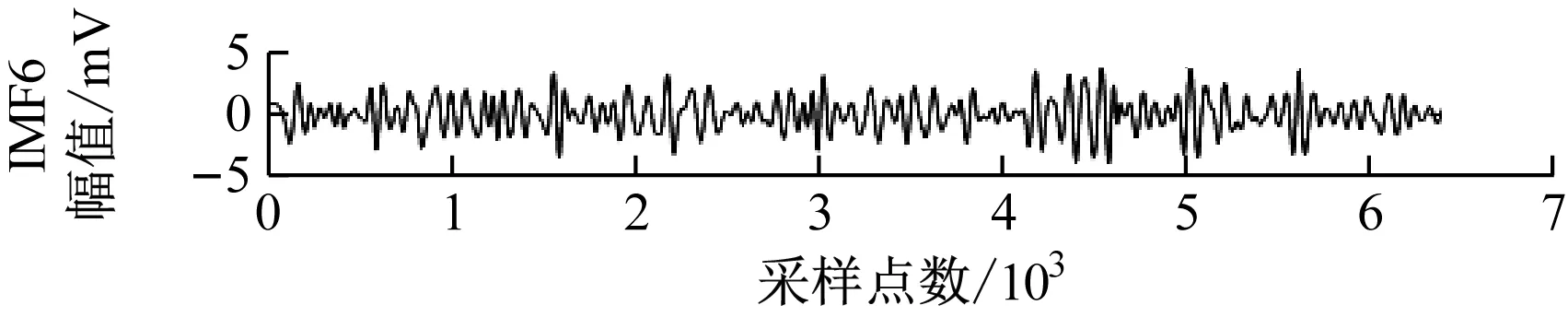
图5 信号s1 CEEMD分解

对信号s1，s2的IMF分量进行分析，分别求各IMF分量与原信号的相关系数及各IMF分量峭度，结果见表3和表4。综合考虑峭度和相关系数来选取最能反映轴承故障特征的IMF分量。选取信号s1的IMF1、IMF2分量，信号s2的IMF1分量，作为小波包分解树的重构系数，得到小波包重构信号。

图6 信号s2 CEEMD分解

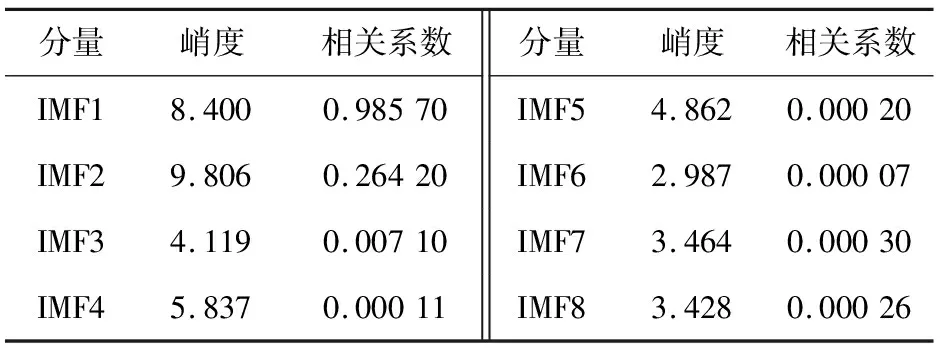
表3 信号s1 经CEEMD分解后的IMF分量

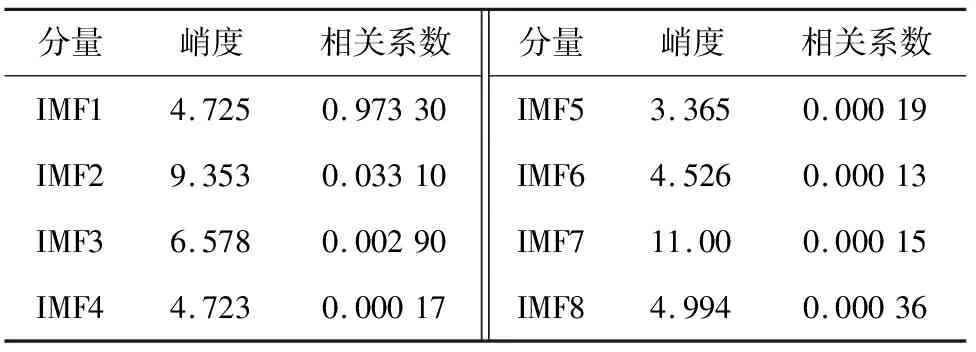
表4 信号s2 经CEEMD分解后的IMF分量

3.2.3 故障特征提取

对重构信号进行Hilbert和傅里叶变换，得到其包络谱，如图7所示。从图7可看出，重构信号包络谱只含有转频(30 Hz)、2倍转频(60 Hz)、内圈故障特征频率(161.9 Hz)及其2次谐波(323.7 Hz)、3次谐波(485.6 Hz)，故障特征频率明显，能够准确判断出轴承内圈出现故障。

采用传统包络信号解调分析方法，即对原始轴承内圈故障信号进行解调，结果如图8所示。从图8可看出，用传统解调算法能够检测到内圈故障特征频率(161.9 Hz)，但在特征频率及其谐波附近出现了接近幅值的干扰频率。故障特征频率淹没在噪声等其他谱线中，不利于故障特征提取。

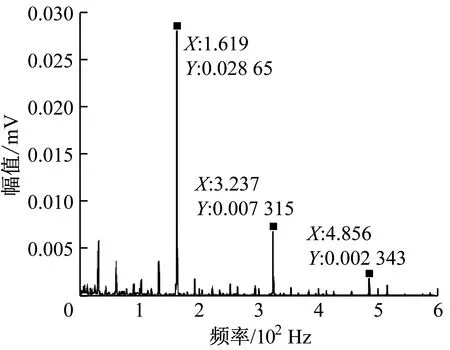
图7 内圈故障重构信号包络解调

图8 内圈故障信号包络谱

3.3 轴承外圈故障信号分析

为验证所提算法的可靠性，将其应用于轴承外圈故障特征提取中。对外圈故障信号进行快速谱峭度分析，结果如图9所示。从图9可看出，最大峭度频带中心频率为2 875 Hz，带宽为250 Hz，频率在[2 625 Hz，3 125 Hz]范围内的谱峭度最大，对该频率范围内的信号进行滤波分析，得到滤波后的频域信号，如图10所示。

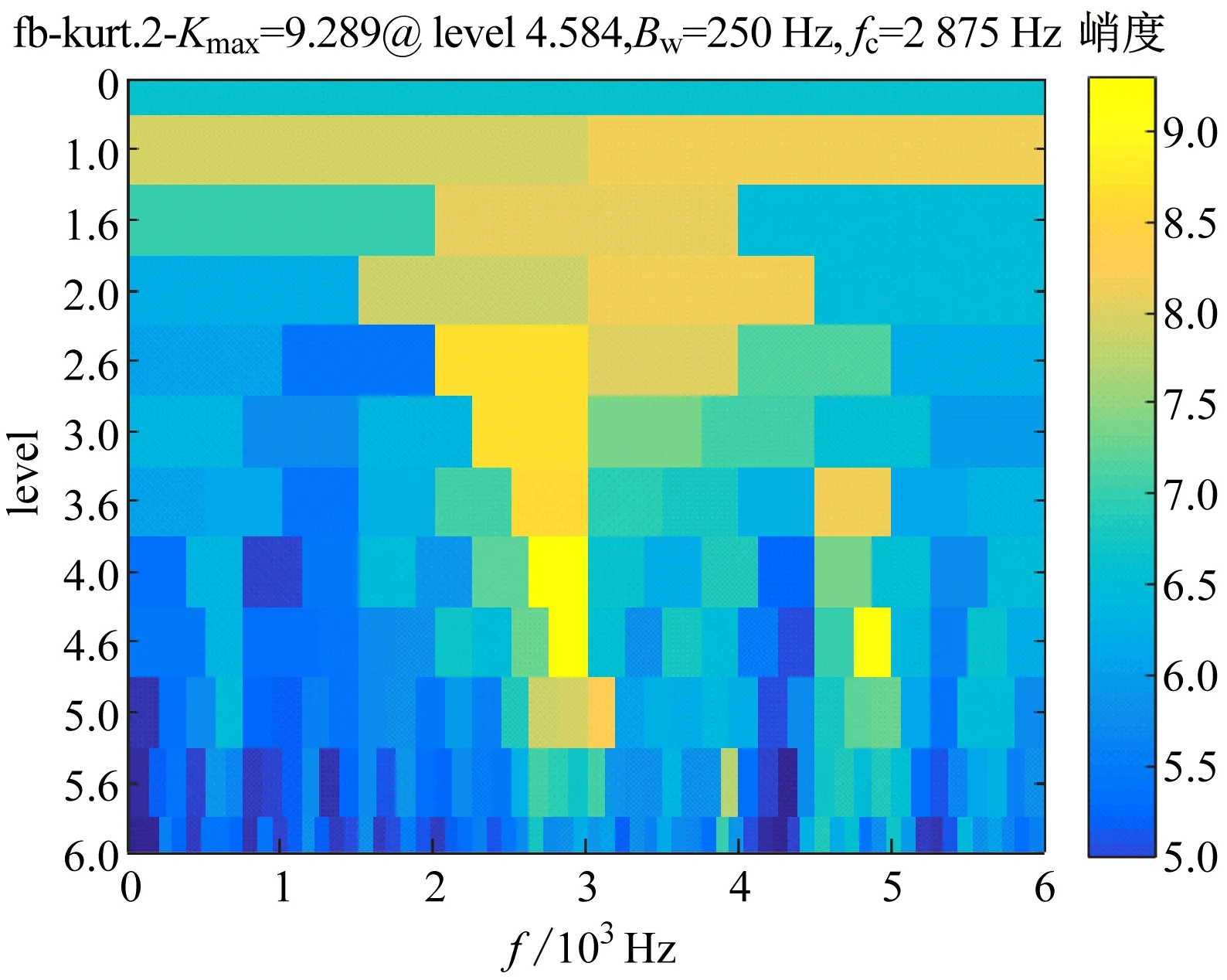
图9 外圈故障信号谱峭度

选择db5小波基对轴承故障信号进行1层小波包分解，分解结果包含低频近似信号s3和高频细节信号s4两个部分。分别对信号s3，s4进行CEEMD分解并对得到的IMF分量进行分析，分别求各IMF分量峭度及其与原信号的相关系数，选取信号s3的IMF1和信号s4的IMF1分量作为小波包分解树的重构系数，得到小波包重构信号。对重构后的信号进行Hilbert和傅里叶变换，得到其包络谱，如图11所示。从图11可看出，重构信号包络谱只含有转频(30 Hz)、外圈故障特征频率(107.7 Hz)及其2次谐波(215.3 Hz)、3次谐波(323 Hz)，能够滤除干扰成分，外圈故障特征频率明显，能够准确判断出轴承外圈故障。

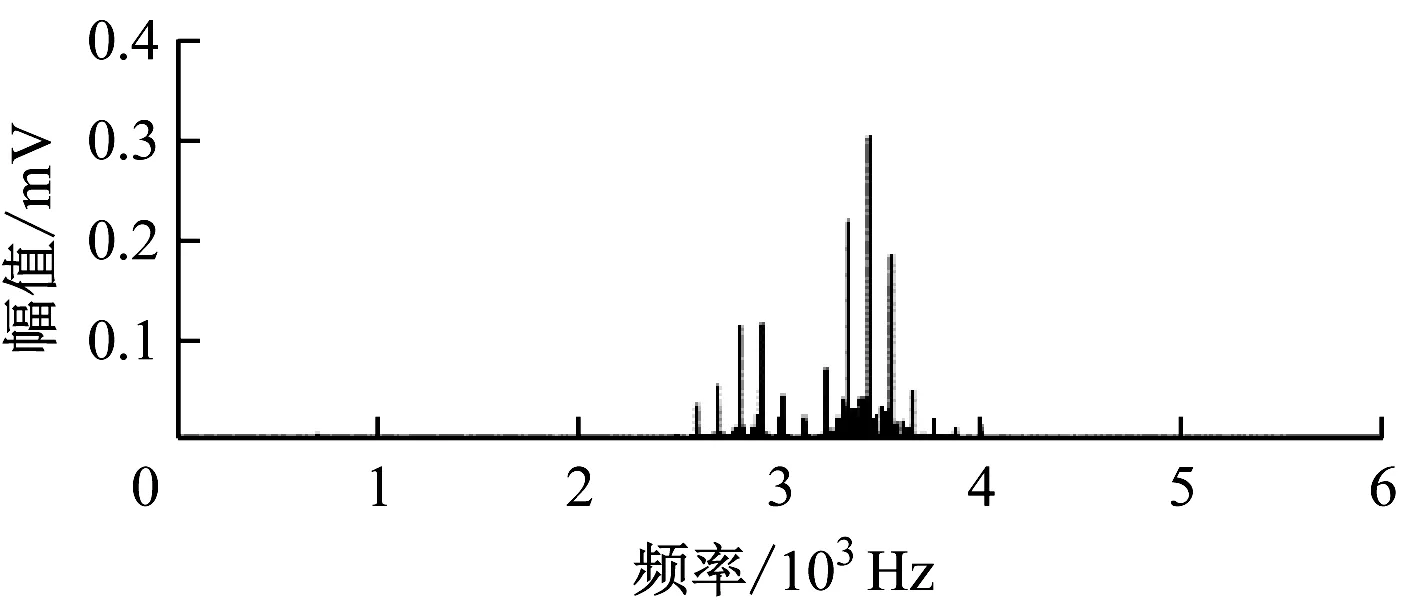
(a)滤波前

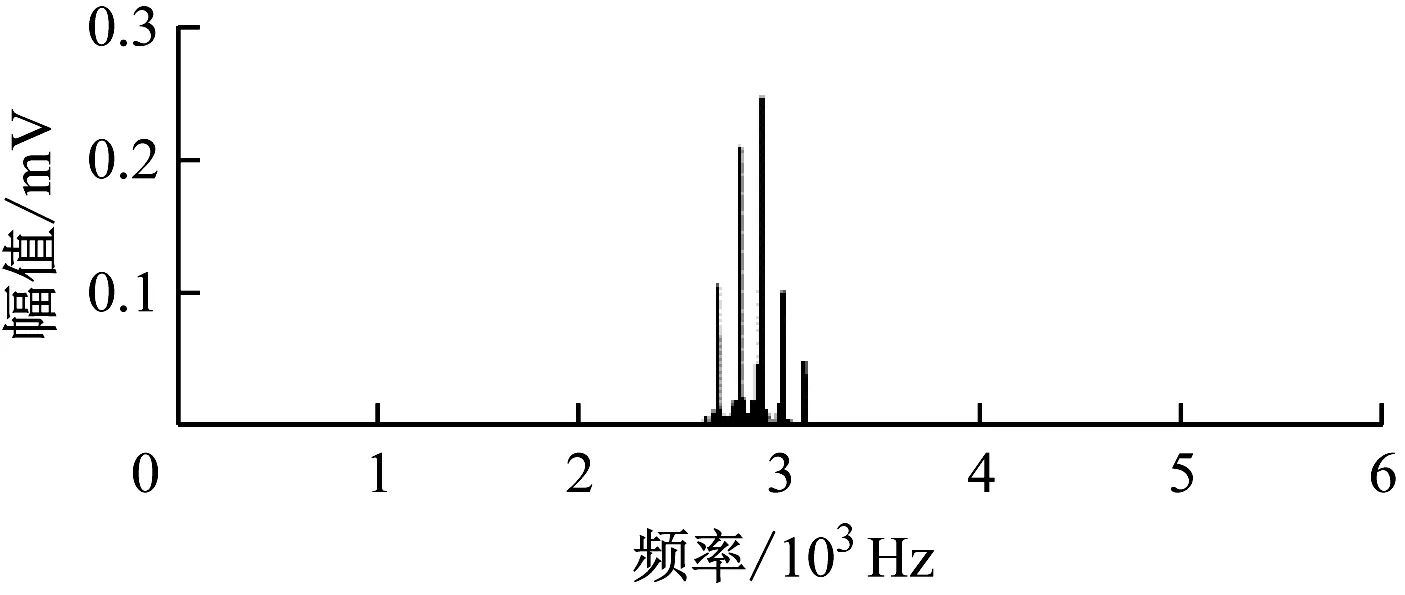
(b)滤波后

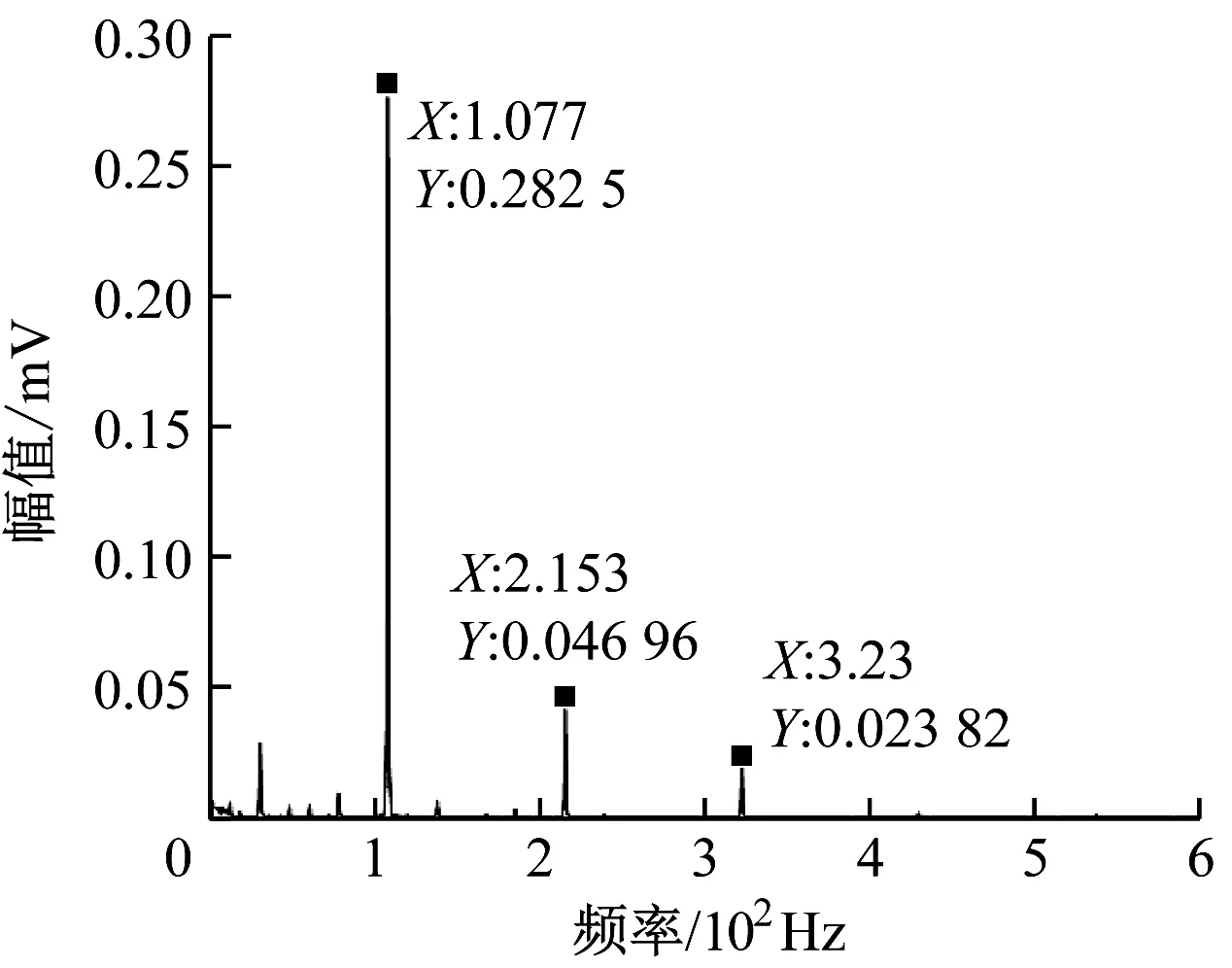
图11 外圈故障重构信号包络解调

采用传统包络信号解调分析方法，即对原始轴承外圈故障信号进行解调，结果如图12所示。从图12可看出，传统包络解调谱线能够检测到外圈故障特征频率(107.7 Hz)，但同样在特征频率及其谐波附近出现接近幅值的干扰频率。故障特征频率谱线不突出，不利于故障特征提取。

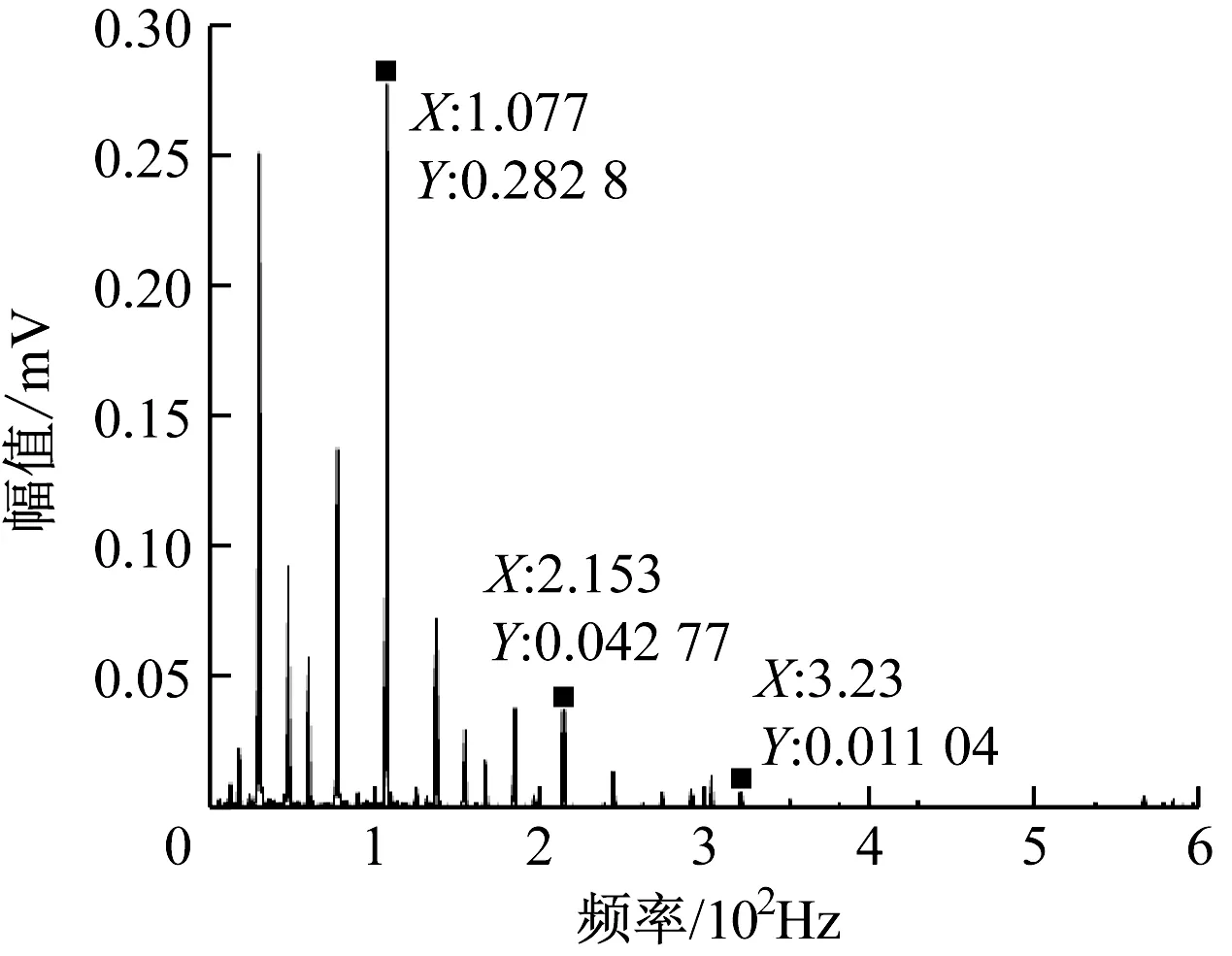
图12 外圈故障信号包络谱

综上，本文提出的方法能够有效提取轴承故障特征频率，对于早期微弱轴承故障信号能够及时、准确进行预判诊断。

4 结语

(1)对传统包络解调算法进行改进，提出了基于小波包分解和CEEMD的轴承早期故障特征提取方法。对原始信号进行谱峭度分析，优化滤波器设计，降低了背景噪声的干扰，同时最大限度保留轴承故障特征信息。

(2)将CEEMD与小波包分解相结合，应用于轴承早期故障检测，解决了经典EMD分解存在的模态混叠、无效分量问题；利用小波包分解对数据进行多层次分析，增强故障冲击信号，准确提取特征频率，避免信号能量损失。

(3)仿真结果表明，相较于传统包络解调算法，重构后信号的背景噪声得到抑制，故障特征分量突出，验证了所提方法的可行性、有效性。限于实验条件，无法对煤矿实测数据进行分析，下一步工作重点是对实测数据进行故障特征识别，将算法移植到嵌入式平台，对轴承运行状况进行实时监控。