基于半监督MPSVM的电力系统暂态稳定评估

曲锐，王世荣，辛文龙

(1.广东电网有限责任公司佛山供电局，广东 佛山 528000；2. 长春工业大学 电气与电子工程学院，吉林 长春 130000)

暂态稳定评估是电力系统安全稳定分析方法的重要组成部分[1]。随着我国电力系统规模的不断扩展，新能源的大规模并网、电力电子设备的广泛应用、大区域互联系统的复杂程度不断提高，给电网稳定运行带来严峻挑战，为避免类似美国、加拿大、西欧大停电事故的再度发生[2]，寻求准确有效的电力系统暂态稳定评估方法具有重要意义[3]。

目前，暂态稳定评估方法主要以时域仿真[4]为主、直接法[5]为辅。时域仿真法具有较高的准确性，而直接法可寻求系统暂态稳定裕度等优点，已在电力系统暂态稳定评估领域得到了大量研究和应用，并取得很多研究成果[6]。随着研究的深入，时域仿真法和直接法2项技术框架的不足也逐渐显现出来，主要包括：①时域仿真法需要求解电力系统的大量代数和非线性方程，具有计算速度较慢和无法定量描述的不足，很难满足在线实时评估的实际需求[4]；②直接法在确定稳定裕度时，极限能量的求取受非线性时变因素的影响，无法适应复杂的系统网络拓扑，通用性很差。人工智能方法兼顾时域仿真和机器学习的优势[7-11]，具有精度高、耗时短、维度低等优点，已在电力系统实时评估中得到广泛应用[12-14]。

现有支持向量机(support vector machine, SVM)[15-16]、广义特征值近端支持向量机(generalized eigenvalue proximal support vector machine, GEPSVM)等人工智能方法为监督学习模式，其泛化性能依赖于是否具有足够的样本标记信息[17-18]，只采用有标记的样本数据进行模型训练；然而，现实世界中的许多学习问题，例如自然语言分析[19]、垃圾邮件过滤[20]等有标记数据的获取通常较困难，而未标记数据的收集更容易，当标记信息量不足时监督分类器的评估性能则不是很理想。电力系统暂态稳定的历史状态信息很难表征复杂多变的稳定状态情况，而广域量测信息可很好地表征系统运行情况，且广域量测数据相对容易获取；因此，电力系统暂态稳定评估的标记数据不足或不准而未标记数据无法充分利用问题急需解决。

为解决大量未标记数据和较少标记数据的暂态稳定评估模型训练问题，可采用半监督学习进行模型训练[17]。流形正则化(manifold regularization，MR)具有较好的优化结构[21]，其在MR框架中引入了2个正则化项，分别用于处理分类器的复杂性和流形的平滑性。文献[22]首先将监督非平行近端分类器扩展到半监督模型，并提出拉普拉斯孪生SVM，实验结果可证明其有效性；但拉普拉斯孪生SVM的挑战在于2个高维二次规划问题的求解，计算效率较低。

针对上述问题，提出一种半监督近似流形支持向量机(manifold proximal support vector machine，MPSVM)用于暂态稳定评估模型，该模型不仅引入MR技术从输入样本数据内部捕获尽可能多的几何信息，并通过最大距离理论表征电力系统稳定类和不稳定类之间的差异，即：①通过求解2个特征值问题确定最优超平面，有效避免复杂的矩阵求逆计算；②采用贝叶斯非线性分层模型进行参数优化，有效提高评估性能；③MPSVM可充分利用无标签进行模型训练，有效提高数据利用率和评估性能。采用IEEE 39标准系统和鞍山电网的仿真分析验证所提评估模型的有效性和准确性。

1 近似流形支持向量机

1.1 MPSVM的基本原理

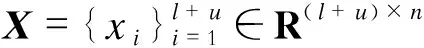
采用二维样本来分析不同分类器的分类原理，此处每个样本包含2个特征，横轴为特征1取值范围，纵轴为特征2取值范围，如图1所示。假设120个样本中只有3个有标签样本(包括2个正类和1个负类)，其余样本为无标签样本，如图1(a)。如果仅采用这3个有标签样本进行模型训练，SVM和GEPSVM最优超平面训练结果如图1(b)和图1(c)所示，误分类的几率较大，而利用无标签和有标签样本的训练结果如图1(d)，可有效改善评估性能。

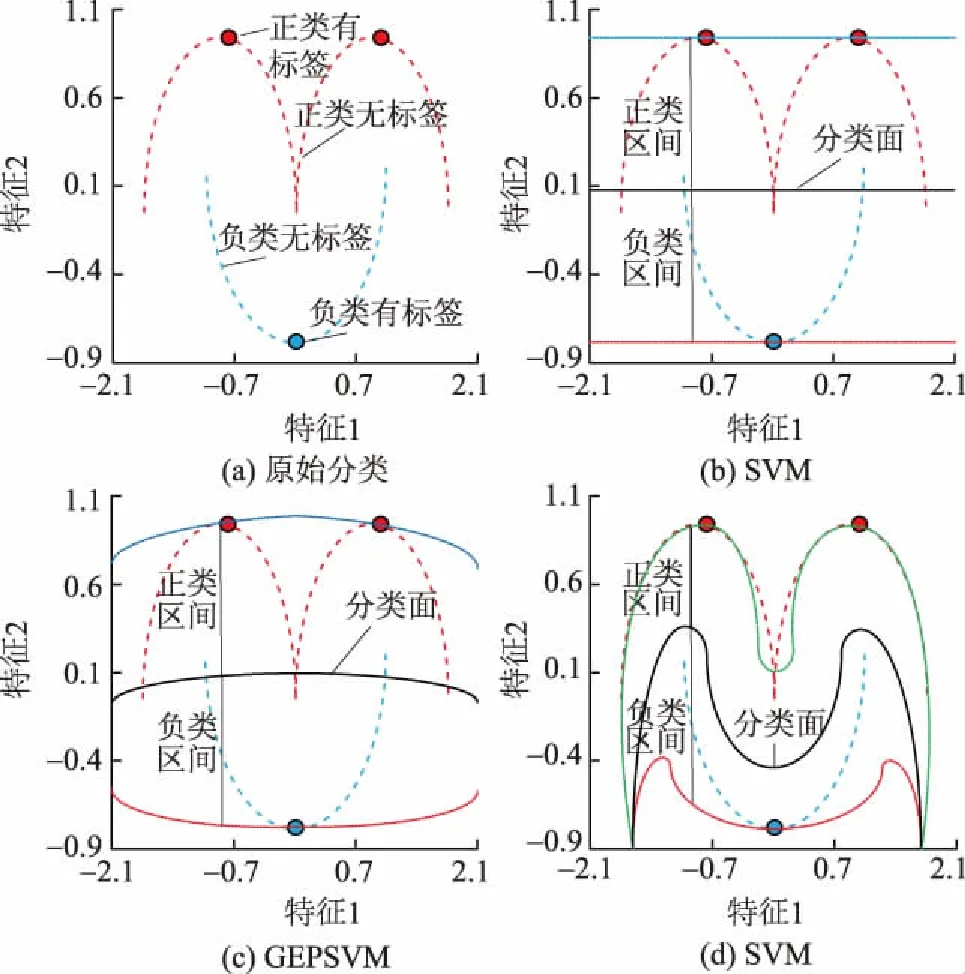
图1 分类器SVM、GEPSVM和MPSVM的分类原理Fig.1 Classification principles of SVM, GEPSVM and MPSVM

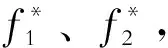
(1)

(2)

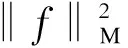
鉴于暂态稳定评估的模型构建为非线性优化问题，特引入MPSVM的非线性模型。利用2个核函数构建近端超平面：

(3)

式中：X′为输入样本数据矩阵的转置;x′为输入样本矩单个样本的转置;ω1和ω2为法向量分量；b1和b2为偏差分向量；K(·,·)为核函数，例如径向基核函数K(u,v)=e-γ‖u-v‖2,核参数γ>0，进而可得如下所示MPSVM的非线性优化问题：

(4)

(5)

式中：A∈Rm1×n和B∈Rm2×n分别为正类“+1”和负类“-1”有标签样本，m1+m2=l；e1、e2、e为单位矩阵；c1>0为经验风险惩罚参数;c2>0为MR参数;L为拉普拉斯乘子。

令Hφ=[K(A,X′)e1]，Gφ=[K(B,X′)e2]，Jφ=[K,e]，v1=[ω1;b1]，v2=[ω2;b2]，上述优化问题可转化为：

(6)

s.t.‖v2‖2=1.

(7)

可通过求解如下方程的特征值λ1、λ2和特征向量，来确定式(6)和式(7)优化问题的解：

(8)

(9)

优化问题的最优解即为式(8)和式(9)最小特征值的特征向量。进而确定(ω1,b1)和(ω2,b2)，当输入测试样本x∈Rn，类别标号为i(i=“+1”,“-1”)，并可以通过如下判别函数来确定分类结果：

(10)

1.2 基于贝叶斯非线性分层模型的最优参数选择

贝叶斯非线性分层模型可通过最大化参数分布的后验，确定最优参数值。贝叶斯非线性分层模型的推断过程[23]如图2所示。

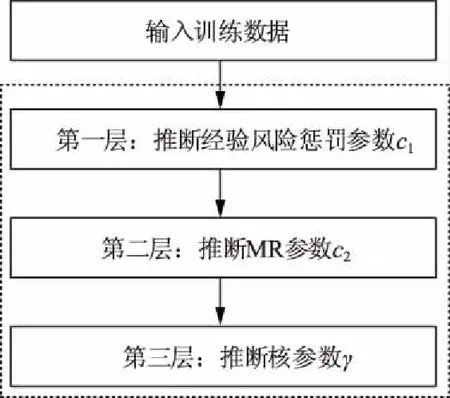
图2 贝叶斯非线性分层模型Fig.2 Bayesian nonlinear layered model

1.2.1 第一层推断

第一层贝叶斯推断可解释为经验风险惩罚参数c1的贝叶斯推断。将式(6)和式(7)的分类模型定义为H，训练数据集用D表示，D的分布为p(D|c1,c2,H)，参数的先验概率为p(D|c2,H)，假设正则化参数c2给定，经验风险惩罚参数c1的后验概率可通过贝叶斯准则的第一层推断获得，若训练样本独立同分布，且p(D|c1,c2,H)服从高斯分布，则贝叶斯式如下：

(11)

假设

(12)

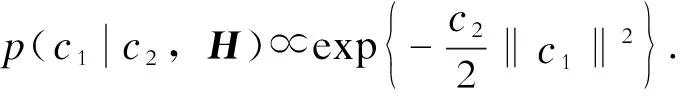
(13)

得到：

(14)

(15)

式(11)—(15)中：yi为第i个样本的输出数据；Cconst为常数。

式(15)的后2项与经验风险惩罚参数c1无关，因此式(15)的优化训练结果可转化为最大化c1的后验概率，进而获得c1的最优值c1MP。

1.2.2 第二层推断

第二层贝叶斯推断可解释为MR参数的贝叶斯推断，通过最大化p(c2|D,H)∝p(D|c2,H)p(c2|H)来选择MR参数c2。假设p(c2|H)平坦，正则化参数c2可由最大化p(D|c2,H)来确定。若在c1=c1MP时，正则化参数的后验概率服从高斯分布，则c2可通过对c1积分求得：

(16)

其中:

(17)

而Ec1,MP、ED,MP分别为Ec1、ED在c1=c1,MP时的取值，由文献[6]可知c2的最优值不必通过最大化lnp(D|c2,H)求解，只需令式(16)对c2偏导数为零,即

2c2Ec1,MP=γ.

(18)

式中γ=k-c2tranceΛ-1。

(19)

(20)

式中：I为单位矩阵；T为调制矩阵；φ(xi)为中继调制矩阵。

若用ρi表示Z的特征值，通过对矩阵进行特征向量分解，可得到：

(21)

(22)

式中k为调制因子。

进一步计算p(D|c2,H)的值，并通过迭代计算得到MR参数c2的最优取值。

1.2.3 第三层推算

第三层贝叶斯推断可解释为核参数的贝叶斯推断，可通过计算模型训练数据集D的后验概率和贝叶斯参数估计理论对核参数进行推断估计，获得MPSVM核参数的最佳值。D的后验概率为

(23)

2 基于MPSVM的暂态稳定评估

2.1 构建原始特征集

同步相量测量单元作为现代电力系统的量测仪器，可持续不断地采集系统运行数据,见表1[24]。

表1 同步相量测量单元数据Tab.1 Synchronization phasor measurement unit data

由故障后的实测数据，构建表征电力系统动态特性的原始特征集[8]，并应用特征选择方法对原始特征集进行特征压缩，进而确定与暂态稳定特性具有较大强相关的12维特征，见表2,其中包含故障初始时刻t0和故障清除时刻tcl的系统特征。

表2 数据集的输入特征量Tab.2 Inputcharacteristic quantity of the data set

由多次故障实测数据确定的特征集，构建成电力系统暂态稳定评估的样本集，并将样本集随机分为用于模型训练的训练集和模型有效性验证的测试集，采用第1.1节介绍的MPSVM进行电力系统暂态稳定评估。

2.2 暂态稳定评估流程

由上述分析可知，本文所提MPSVM评估方法的暂态稳定评估流程如图3所示，其中ROC为接受运行特性曲线。

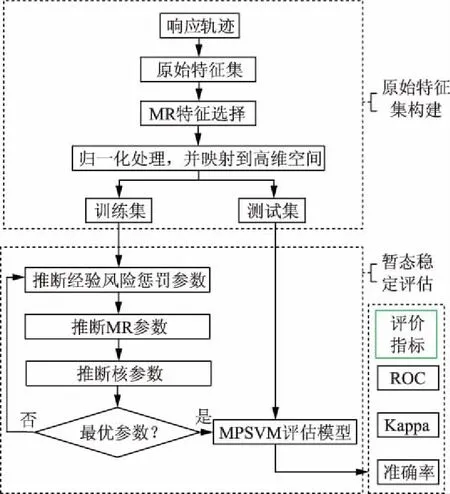
图3 暂态稳定评估流程图Fig.3 Transient stability assessment flow chart

评估流程主要分为3步：①采用特征选择方法对原始特征集进行特征压缩；②采用贝叶斯非线性分层模型优化参数，改善评估性能；③基于训练集对MPSVM进行离线训练，构建暂态稳定评估模型，同时计算评价指标值。

2.3 评价指标

准确率指标定义为评估正确样本数与样本总数的比。Tij表示第i类被评估为j类样本数，其中i={0,1}，j={0，1}，则准确率为

(24)

统计值指标D可用于评价评估分类和实际分类的一致性，即

(25)

接受运行特性曲线(receiver operating characteristic curve，ROC)指标R包括评估结果的误报率(false positive rate，FPR)函数fFPR和评估结果的命中率(true positive rate，TPR)函数fTPR，且：

(26)

(27)

综合评价指标可表征所提分类器模型在不同评价角度的平均性能，且

(28)

3 算例分析

3.1 IEEE 39节点系统

利用电力系统仿真软件PSD-BPA进行仿真计算获得电力系统的潮流和稳定运行数据，发电机采用二阶模型，负荷为恒阻抗负荷，故障类型为三相短路，故障开始和清除时刻分别为0.1 s和0.3 s，图4为IEEE 39的系统图，其中G表示发电机。

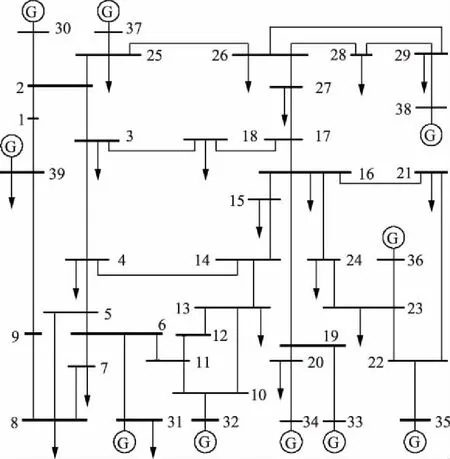
图4 新英格兰10机39节点系统Fig.4 New England 10-machine 39-node system

将测试系统的相对功角差最大值Δδmax作为暂态判据，Δδmax≥360°表示系统失稳；Δδmax<360°表示系统稳定。把获得的2 400个样本构成样本集，随机选取样本集中的1 200样本用于构建评估模型，其余样本用于暂态稳定评估来获得评价指标。该算例分析如下：

a)MPSVM评估模型的准确性分析。采用4种分类器进行暂态稳定评估，4种分类器包括C-SVM、nu-SVM、GEPSVM和MPSVM，评价结果见表3。

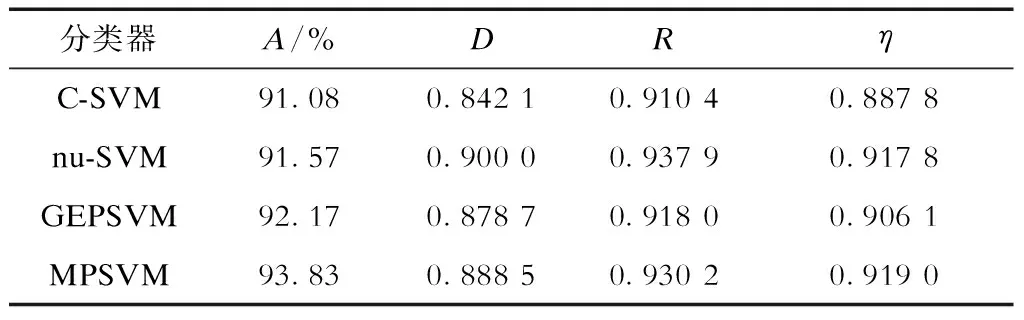
表3 4种分类器的评价指标Tab.3 Evaluation indicators of 4 classifiers

由表3可知:对比准确率指标A、ROC指标R、D指标，可以发现MPSVM的准确率为93.83%，综合评价指标值η为0.919 0，均分别高于其他3种分类器，但准确率指标未超过95.00%，初始参数时评估性能有待进一步提升。

b)利用贝叶斯非线性分层模型优化参数提高评估性能。通过贝叶斯非线性分层模型的第二层推断确定最优MR参数及第三层推断确定最优核参数后MPSVM的暂态稳定评估性能，见表4。

表4 贝叶斯参数优化后MPSVM的评估精度Tab.4 Evaluation accuracy of MPSVM after Bayesian parameter optimization

由表4可知：经过贝叶斯非线性分层模型优化参数后的总体评估性能有所改善，第一层优化后由93.83%提高到94.40%，综合指标由0.919 0提高到0.925 0，比未优化前略有提高；第二层优化选取最优MR参数后，评估准确率由94.40%提高到95.25%，综合指标由0.925 0提高到0.934 6；第三层进一步优化选取最优核参数后，评估准确率由95.25%进一步提高到96.83%，综合指标由0.934 6进一步提高到0.957 6。可见不同参数对评估性能的影响较大，合理选择参数对提高评估准确率具有重要意义。贝叶斯参数优化后4种分类器的评估精度见表5。由表5可知经贝叶斯参数优化后C-SVM、nu-SVM和GEPSVM的综合评价指标都有所提高，但仍低于MPSVM的综合评价指标，进一步说明MPSVM较现有分类器具有更高的评估性能。

c)MPSVM的核函数分析。采用3种核函数分析其对MPSVM分类器的影响，3种核函数包括多项式、线性和径向基核函数，不同核函数的评价指标见表6。

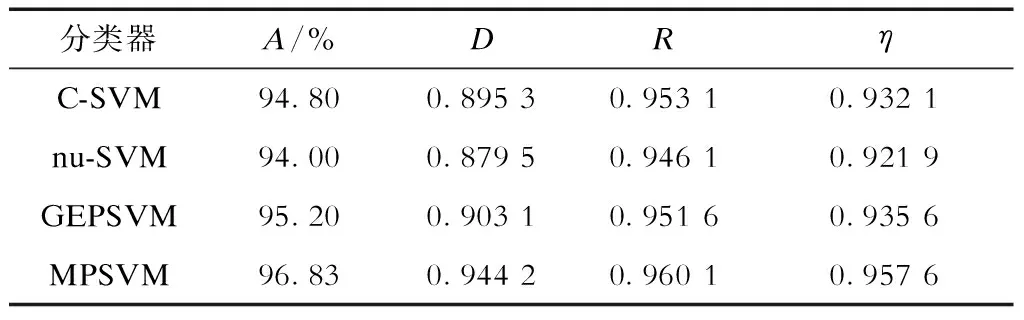
表5 贝叶斯参数优化后4种分类器的评估精度Tab.5 Evaluation accuracy of 4 classifiers after Bayesian parameter optimization

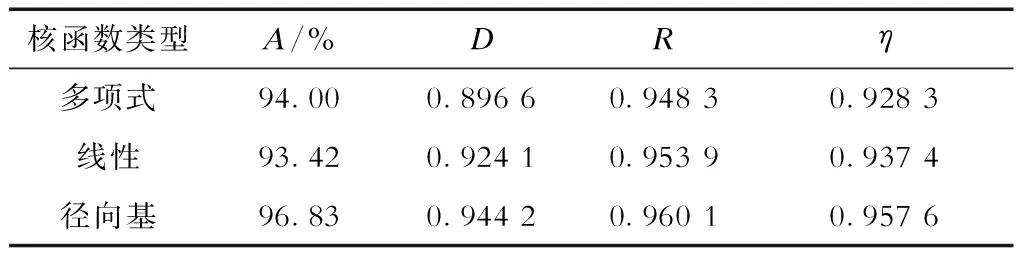
表6 3种核函数的MPSVM评价指标Tab.6 MPSVM evaluation indicators of three kernel functions

由表6可知：MPSVM采用多项式核函数的综合评价指标为0.928 3，在3种核函数中的综合评价指标最小，但也高于表3中C-SVM、nu-SVM和GEPSVM的综合评价指标；采用径向基核函数的综合评价为0.957 6，具有最高的综合评价指标，因此可选择径向基核函数作为MPSVM的核函数。

3.2 鞍山电网实际系统

鞍山电网地处辽宁电网中南部，随着辽宁电网的快速发展，网架结构不断加强，复杂性也不断加剧，其整体稳定性问题不断出现，鞍山电网的区域接线如图5所示。

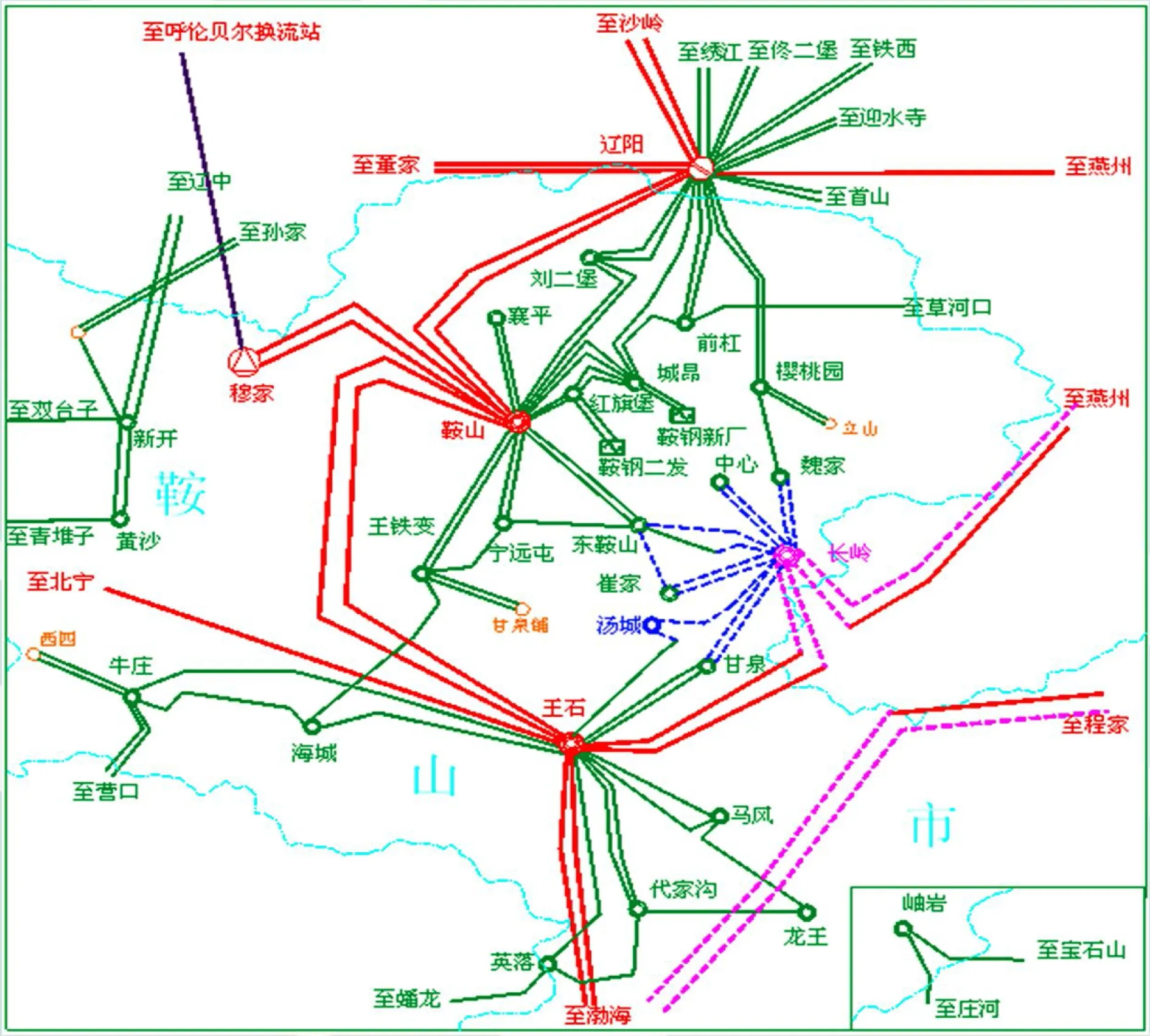
图5 鞍山电网地区接线图Fig.5 Anshan power grid area wiring diagram

从鞍山电网共获得1 000样本来构成样本集，随机选取样本集的3/4作为训练集，其余作为测试集，暂态稳定评估结果见表7。

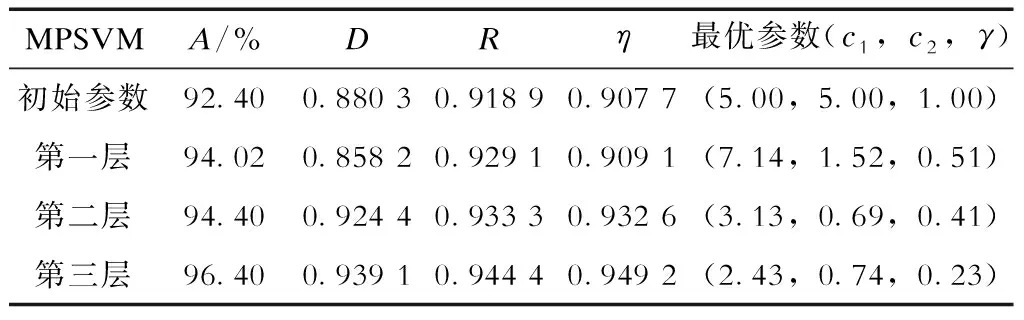
表7 鞍山电网的暂态稳定评估结果Tab.7 Transient stability assessment results of Anshan power grid

由表7可知:在鞍山电网中通过贝叶斯非线性分层模型进行第一层参数优化后，评估准确率由92.40%提高到94.02%；第二层优化选取最优MR参数后，评估准确率由94.02%提高到94.40%，综合指标由0.909 1提高到0.932 6；第三层优化选取最优核参数后，评估准确率由94.40%提高到96.40%，综合指标由0.932 6提高到0.949 2。可见在实际系统通过合理选择参数可有效提高评估准确率。

4 结论

本文提出一种基于半监督MPSVM的电力系统暂态稳定评估方法，通过IEEE 39标准系统和鞍山电网的仿真分析，得出如下结论：

a)根据广域量测信息采集的故障后信息，计算与电力系统稳定性相关的原始样本集，并采用特征选择方法进行特征压缩，可在原始样本集的基础上搜索最优特征子集，进一步减少特征冗余信息，降低特征维数。

b)利用贝叶斯非线性分层模型确定MPSVM的最优参数，可有效改善暂态稳定评估的性能，分析不同核函数的评估性能，同时得出径向基核函数具有最高的评估准确率。

c)采用半监督学习模式，可有效利用无标签样本数据信息，提高评估准确率，相较于现有分类器SVM、GEPSVM等具有较高的评估性能。

本文所提的暂态稳定评估方法可有效利用电网的无标签数据信息来提高评估准确率，可以作为电力系统暂态稳定预警的基础。如何将所提方法应用含大规模风电并网系统的暂态稳定评估，将是下一步工作的重点。