一类抽象函数试题的命题手法探究
杨苍洲 许银伙
(1.福建省泉州第五中学 362000;2.福建省泉州外国语中学 362000)

从题设的结构展开联想,一般可以顺利构造出新函数,并使该新函数的导函数已知.但是,在寻找原函数的过程中却遇到原函数不容易找出,甚至无法找出的麻烦.
那么,这类问题如何解决呢?下面我们来研究其解题方法和命题手法.

A.有极大值,无极小值
B.有极小值,无极大值
C.既有极大值又有极小值
D.既无极大值又无极小值


因此,当x>2时,h′(x)>0,h(x)单调递增;当0 又h(2)=e2-2g(2)=e2-2[23×f(2)]=0,所以h(x)≥0,f′(x)≥0,故f(x)在(0,+∞)单调递增.因此f(x)既无极大值,又无极小值,选D. 结合对试题的解题手法的研究,笔者认为此类试题的命题方法如下,可分五步完成. 步骤一:设定两函数f(x),g(x)的关系.如,本题中设定g(x)=x3f(x). 步骤四:设定f(x)的单调性、极值情况.如,本题设定f(x)在(0,+∞)单调递增. 现只需h(x)=ex-3g(x)恒大于等于0,下面研究函数h(x). 根据对此类问题的命题手法的研究,笔者尝试以此手法进行试题的命题创作: 首先,我们设定g(x)=x2f(x),g′(x)=x2lnx.因此可得 [x2f(x)]′=x2lnx,即得xf′(x)+2f(x)=xlnx. 接着,我们来研究f(x)在(0,+∞)可能的单调性与最值情况,据此设置其他条件并进行选项的设定. 下面研究函数h(x)=x3lnx-2g(x)的情况,由h′(x)=3x2lnx+x2-2g′(x)=(lnx+1)x2. 整理可得试题如下. A.f(x)在(0,+∞)上单调递增 B.f(x)在(0,+∞)上单调递减 答案:A. 一道新题的诞生,让我们体验了成功的喜悦,却又意犹未尽.于是,我们让思维再次扬帆起航,再次走进命题的世界. 接着,我们来研究f(x)在(0,+∞)可能的单调性与最值情况,据此设置其他条件并进行选项的设定. 由f(x)=g(x)·ex,得f′(x)=[g′(x)+g(x)]ex=[exlnx+g(x)]ex. 下面研究函数h(x)=exlnx+g(x)的情况. 又因为f′(x)与h(x)同号,现设定f′(1)=h(1)=0,此时g(1)=0,f(1)=0. 当x>1时,f′(x)>0,f(x)单调递增;当0 整理可得试题如下. 新题2:设定义在(0,+∞)的连续可导的函数f(x)的导函数是f′(x),且满足f′(x)-f(x)=e2x·lnx,f(1)=0,则x>0时,( ). A.f(x)在(0,+∞)上单调递增 B.f(x)在(0,+∞)上单调递减 C.f(x)有最小值0 D.f(x)有最大值0 答案:C一、命题方法探究



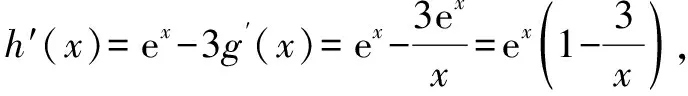
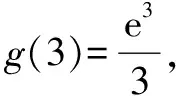

二、新题命制








