倡导教学评一致性 提升高三数学复习效率——以多面体外接球问题微专题为例

陈建设

(福建省南安第一中学 362300)

教学评一致性，指的是教师的教、学生的学以及统辖在一个标准之下的对教与学的评价，具有高度的相关性.具体而言，就是教什么、学什么、考什么是一致的；如何教、如何学、如何考是一致的；教到哪种程度、学到哪种程度、考到哪种程度是一致的；教学设计、教学实施、教学效果是一致的.高三数学复习课的常见误区就是重视知识面的覆盖而轻视知识点的落实，这与教学评一致性的思路是相背的，因此，笔者建议在高三复习过程中，可针对高考热点和学生的知识薄弱点开展微专题复习，下面就是以多面体外接球问题为例的高三数学复习微专题.

典型题例

例2(2012·课标卷·11)已知三棱锥S-ABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，SC为球的直径，且SC=2，则此棱锥的体积为( ).

图1

详解示范

图2

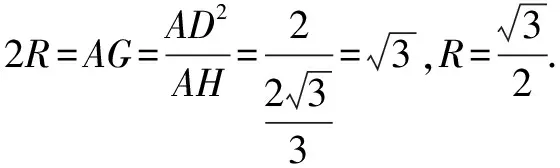
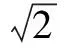
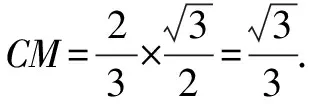
图3 图4

图5

解后反思立体几何是高中数学的重点内容，是考查空间想象能力的重要载体.与球有关的问题是考查的重点之一，求多面体外接球半径的常见方法如下：

(1)勾股定理法 (通性通法，也是高考最常考的)

①思路：关键是找球心，画出截面图，构造与R有关的直角三角形(如图5).②说明：球心在过多面体各面外心且垂直该面的垂线上，其中，直角三角形外心在斜边中点，锐角三角形外心在三角形内，钝角三角形外心在三角形外. (如图6)

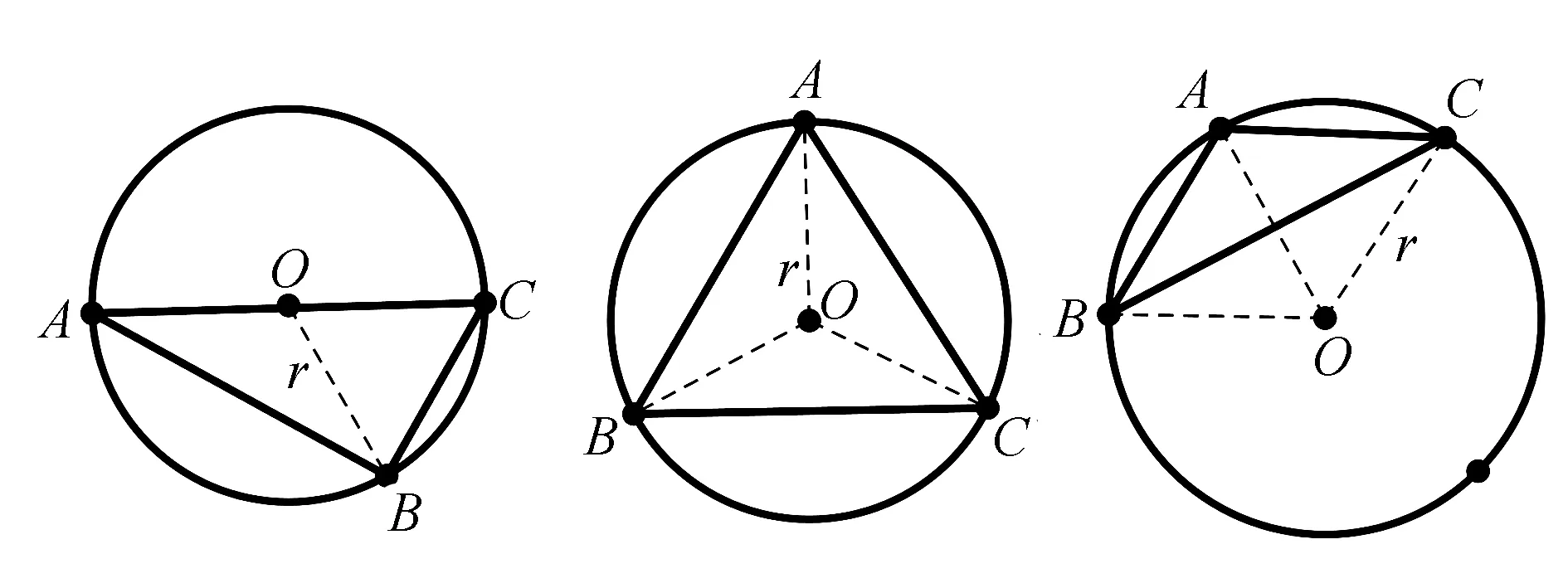
图6

(2)补形法(适用特殊棱锥)

①三棱锥的三条侧棱两两垂直，可以补形为一个长方体(如图7).②四面体的对棱相等，可以补形为一个长方体(如图8).

图7 图8

③棱锥有一条侧棱垂直底面，可以补形为直棱柱(如图9)

图9