利用Lagrange乘数法求函数最值问题

季佳佳

(浙江省台州市仙居城峰中学 317300)

特别的，若在单约束条件F(x,y,z)=0下，求f(x,y,z)的极值时，只要构造Lagrange函数L(x,y,z)=f(x,y,z)-λF(x,y,z)即可．

一、单约束条件下的最值问题

例1 (2011年浙江) 设x,y为实数，若4x2+y2+xy=1，则2x+y的最大值____．

解方法一

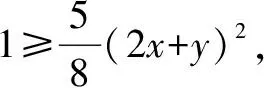
看到这类题，学生的第一反应是用基本不等式的知识去解决，这种思路是对的，但是用不等式的方法是有局限性的，如果碰到更复杂的问题，高中的知识就很难“胜任”，这时，我们就可以看到Lagrange乘数法的巨大威力．

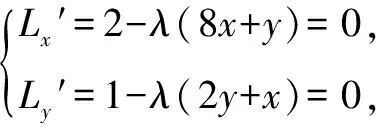
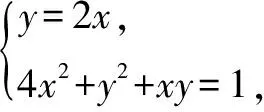
例2 要设计一个容量为V的长方形无盖水箱，试问水箱的长，宽，高各等于多少时，其表面积最小？

解设水箱的长，宽，高分别为x,y,z，则体积V=xyz，表面积S=2xz+2yz+xy．

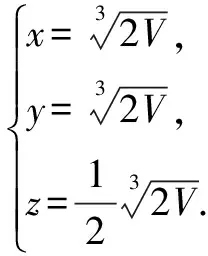
二、双约束条件下的最值问题

例3 (2014年浙江)已知实数a,b,c满足a+b+c=0，a2+b2+c2=1，则a的最大值____．

解由a2+b2+c2=1，得a2+b2+c2-1=0.

构造Lagrange函数L(a,b,c)=a-λ(a+b+c)-μ(a2+b2+c2-1).

以上例子说明了Lagrange乘数法的巨大作用，它能有效回避不等式中复杂的思维过程和代数变形，对提高学生解题能力，树立学生学习数学的信心，拓宽学生思路，提高学生分析问题、解决问题的能力有很大帮助．