恒成立问题中一类难点突破
2020-05-07 03:28:40俞新龙
数理化解题研究 2020年13期
俞新龙
(浙江省绍兴市柯桥区越崎中学 312050)
恒成立问题是高中数学一类重要的题型,大家都学有基本解题针对套路,如f(x)≥a(a为常数)恒成立,则f(x)min≥a;f(x) 综上所述,a≤1-2ln2,从而得实数a的最大值为1-2ln2. 上面每一种情况的讨论不能出任何差错,否则必将前功尽弃!但如果我们用变量分离的方法解该题,则将容易得多. 变量分离也不一定不需要分类讨论,但它确实是一种有效突破方法,请继续看下面例子. 例2设函数f(x)=ax3-3x+1(x∈R),若对任意x∈[-1,1]都有f(x)≥0成立,则a=____. 例3若不等式2xlnx≥-x2+ax-3对x∈(0,+∞) 恒成立 ,则实数a的取值范围是( ). A.(-∞,0) B.(-∞,4] C.(0,+∞) D.[4,+∞) 等价转换函数是否成功的标志是能否求出转换后函数的最值.该题也可以用变量分离法求解如下: 需要注意的是以上突破策略并不是孤立的,有时需要两者配合进行.一、变量分离


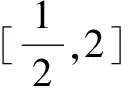
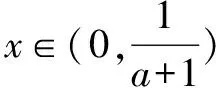

二、等价转换函数
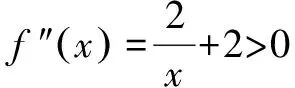

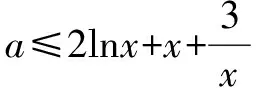
三、利用充分条件

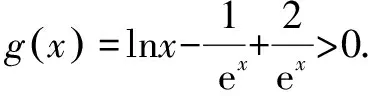

四、作差比较大小
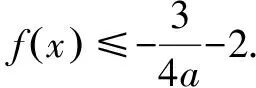

猜你喜欢
新农村(浙江)(2021年9期)2021-09-13 02:55:20
汉字汉语研究(2021年4期)2021-03-09 05:18:54
中华戏曲(2020年1期)2020-02-12 02:29:00
中文信息(2017年12期)2018-01-27 08:22:58
疯狂英语·新策略(2017年7期)2018-01-03 06:51:19
纺织科学研究(2017年8期)2017-09-05 09:46:51
快乐语文(2016年10期)2016-11-07 09:44:43
纺织服装周刊(2016年34期)2016-09-27 02:22:26
中央民族大学学报(自然科学版)(2015年2期)2015-06-09 08:45:18
新课程·小学(2014年7期)2014-10-22 10:08:14

