长大坡道货运列车周期性制动下车轮温升分析

毛保华，龚超奇，张桐，杨彦强

长大坡道货运列车周期性制动下车轮温升分析

毛保华1, 2，龚超奇1，张桐1，杨彦强1

(1. 综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044；2. 北京交通大学 中国综合交通研究中心，北京 100044)

周期性制动是货运列车在长大下坡道运行时的一种常见操纵策略，该过程中车轮会因频繁抱闸而温度上升，过高的温度会危及行车安全。为提高列车运行的安全性，考虑列车周期性制动对热流密度和对流换热系数2个车轮温升关键因素的影响，基于ANSYS软件建立二维车轮“运动—温度”有限元分析模型。对比已有研究实验数据，模型的数字实验结果表明模型有效，且得到：在设定前提下，无电制动力损失时，车轮温度不超过350℃；1台机车电制动力损失和电制动力完全损失时，坡道分别超过−23.7‰和−12.5‰后车轮温度会超过400 ℃；减压量每增加10 kPa，车轮最高温度平均增加13.6 ℃；制动限速每降低5 km/h，车轮最高温度平均降低16.2 ℃。研究结果可为线路坡道设计及电制动失效后的运营组织提供参考。

货运列车；周期性制动；车轮温升；列车管减压量；制动限速

近年来，我国加快了西部地区铁路的建设。西部山区多，地形高差起伏大，铁路线路中经常出现长大坡道。货运列车在长大下坡道运行时，若机车电制动力无法使列车降速，列车将周期性地施加空气制动以控制速度。闸瓦与踏面摩擦时车轮将出现温升现象，过高的温度可能导致车轮损伤和制动效果降低等，危及行车安全。因此，研究长大下坡道货运列车周期性制动车轮温升具有重要意义。车轮温升研究最直接的方法是制动试验，中国铁道科学研究院在1:1制动动力试验台上对Æ915 mm和Æ840 mm货车辗钢车轮进行制动摩擦试验，研究车轮热负荷能力限制[1]。Teimourimanes[2]还进行了地铁列车实际运行试验，通过热电偶采集车轮踏面温度。针对试验方法难以进行参数分析及资金耗费高等不足，有不少学者采用有限元的方法对车轮温升进行研究。彭莉等[3−4]分别考虑列车实际运行数据和列车动力学仿真运行，通过有限元方法模拟了大秦线重载列车全线运行过程中车轮温度场分布。在有限元模型的基础上，针对重载货物列车在长大坡道上紧急制动和恒速制动2种情境下，侯耐[5]研究了车轮和闸瓦的温度变化情况。张金煜等[6−7]考虑车轮周期性旋转时踏面摩擦生热和对流换热交替变化，将旋转热源法与均匀布热法的结果进行对比，并通过试验对结论加以验证；同样考虑非均匀分布的摩擦热流，张乐乐等[8]采用摩擦功率法及摩擦副周向接触长度确定热流密度，分析紧急制动下制动盘的温度场。文永蓬等[9]分析了双S型车轮的弯向、辐板厚度、靠近轮辋处圆弧半径等参数对车轮温升和耦合应力的影响；Walia等[10]还考虑到直线型辐板车轮、运营速度和减速度等。Ertz等[11]考虑将轨道和车轮看作整体，分析车轮沿轨道运动过程中轮轨接触的摩擦热，计算踏面最高温度。许多学者分析了车轮热负荷的影响因素，包括踏面磨耗程度[12]、车辆轴重[13−14]、车轮和闸瓦接触面积[14]。但上述有限元方法主要在列车紧急制动的前提下进行研究，缺乏对列车运行地刻画，也少有周期性制动及相关参数对车轮温度影响的分析。因此，本文以货运列车(2HXD2+50C70，简称列车)为研究对象，在刻画列车长大下坡道周期性制动运行的基础上，利用ANSYS有限元软件建立二维车轮“运动-温度”有限元分析模型，并分析周期制动参数对温升的影响。

1 考虑周期性制动的车轮“运动—温度”有限元分析模型

1.1 周期性制动描述

周期性制动是货物列车在长大下坡道运行时电制动力不足情况下采用的一种安全制动策略，以保证列车速度可控。列车在采取周期性制动时，坡道下滑力大于基本阻力与电制动力之和，仅依靠电制动力无法使列车速度降低，需要周期性地施加空气制动以控制车速，如图1所示。

图1 长大坡道列车周期性制动

本文研究场景为列车制动过程：在指定长度和坡度的下坡道上，列车以制动限速为初速，交替进行制动和缓解地从坡顶运行至坡底。一个完整的制动缓解周期由-减速和-增速2个阶段组成。在点，列车速度达到限速，而仅采用电制动力无法使列车减速；因此，在发挥全部可用电制动力的前提下，以一定的减压量施加空气制动，使列车速度降低。当列车速度降至点时，列车缓解闸瓦以切除空气制动力，在仅施加可用电制动力的情况下增速至限速点；其中，点速度根据-增速阶段列车实际运行时间恰大于列车副风缸恢复至规定压强和制动空走时间来确定。

图1展示了列车运行速度随里程的周期性变化以及制动力的使用情况，该过程可以采用列车运动学方程进行数学化表示。将列车视为刚性质点，并考虑其在无隧道的直线下坡道上运行时，列车运动学方程为：

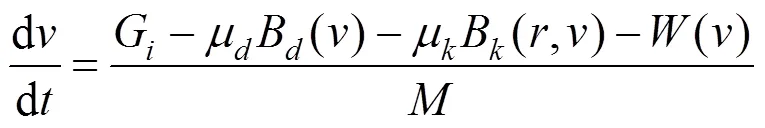
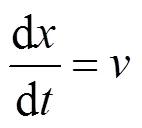
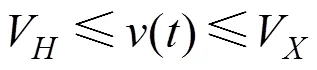
式中：和分别表示列车运行速度和运行里程，与运行时间相关，=()，=()；G表示列车在坡度上的下滑力；为0~2的整数，=2表示2台机车电制动力均正常，=1表示仅1台机车电制动力可以使用，=0表示电制动力完全失效；B()表示速度时一台机车能够发挥的最大电制动力；为0-1变量，=1表示列车处于抱闸制动状态，=0表示列车处于闸瓦缓解状态；表示减压量；B(,)表示速度、减压量时的空气制动力；()表示列车基本阻力表示列车总质量；V和V分别表示最小缓解速度和制动限速，最小缓解速度取10 km/h[15]。

列车经过前一次制动后，需要一定时间等待副风缸空气压强恢复至规定值，才能进行下一次制动。因此，列车增速时间应大于充风时间和空走时间，即：

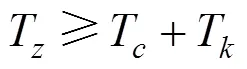
式中：T为列车从缓解速度至制动限速过程的增速时间；T和T分别为列车充风时间和空走时间，按《列车牵引计算》[15]取值。

1.2 车轮有限元模型

车轮有限元模型将车轮离散化为有限数量的单元，再对每个单元的温度进行数值计算，得到车轮温度分布。各网格单元中的最高温度即为车轮最高温度，是以车轮运动随时间变化的。采用ANSYS软件进行模型构建，包括材料参数、几何模型及网格单元、边界条件。

1.2.1 材料参数

材料参数是与温度计算相关的车轮及闸瓦的固有理化属性，包括密度、导热系数和比热。车轮为辗钢车轮，材料密度为7 850 kg/m3，其他材料参数如表1所示。闸瓦为高摩合成闸瓦，材料密度 为2 500 kg/m3，导热系数为1.12 W/(m∙K)，比热为 0.9 J/(kg∙K)。

表1 车轮材料参数

1.2.2 几何模型及网格单元

模型选取直径840 mm的新辗钢车轮，辐板为S型，踏面为标准LM型。由于车轮结构上具有轴对称，并且车轮在列车运行过程中转动速度较快，研究假设输入车轮的摩擦热在闸瓦扫过的踏面圆环面内是均匀分布的，对流换热沿车轮周向也是不变的。因此，车轮温升有限元模型采用二维形式，网格划分采用4节点的二维热单元PLANE55，整体网格大小为4 mm，与闸瓦接触的踏面处的网格为1 mm。最终模型包含1 957个单元和6 204个节点，如图2所示。

图2 二维车轮有限元模型

1.2.3 边界条件

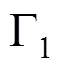
热流边界处热量以热流密度的形式输入车轮，热流密度与列车采用的减压量、运行速度有关。根据摩擦力做功，热流密度可以表示为：

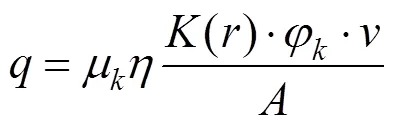
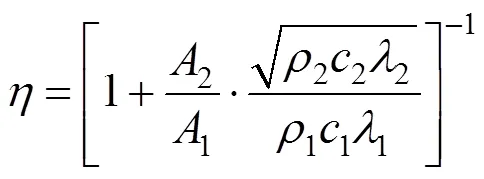
对流换热边界处热量耗散通过对流换热系数反映，列车周期性制动时，影响对流换热系数的主要因素为列车运行速度。因此，对流系数可用经验公式[9]计算：

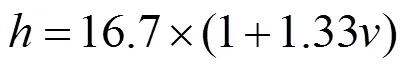
1.3 模型数字实验流程

周期性制动描述列车车轮运动，有限元模型计算车轮温度，式(1)，(5)和(7)通过速度、闸瓦压力、热流密度和对流换热系数将车轮运动和温度联系起来，车轮“运动−温度”有限元分析模型数字试验流程如图3所示。

在“运动−温度”有限元分析模型中，车轮温度是在车轮周期性运动的基础上进行计算的。首先，根据列车周期性制动的减压量、电制动力、坡道、限速及再充风时间等要求，式(1)~(4)分析列车车轮运动，得出各时刻列车速度和闸瓦压力。在此基础上，式(5)~(7)以速度和闸瓦压力计算车轮边界上各时刻的热流密度和对流换热系数。最后，通过ANSYS软件的瞬态热分析功能计算各时刻各网格单元的温度，并统计某时刻各网格单元最高的温度为该时刻车轮最高温度。

图3 模型数字实验流程

1.4 模型验证

为验证模型用于分析列车长大下坡道周期性制动车轮温升的有效性，制动试验所测得车轮最高温度被用于与模型计算结果进行比较。李兰在中国铁道科学研究院制动实验室进行了制动热负荷试验，踏面最高温度平均值为414.6 ℃，最高温度达到446 ℃[13−14]。图4给出了采用上述试验参数时，本文模型与文献[13]试验和计算结果的对比。

图4 本文模型与试验结果对比

由图4可知，文献[13]计算所得车轮踏面最高温度为410.3 ℃，接近多次试验车轮最高温度的平均值414.6 ℃；而本文模型计算所得最高温度为440.3 ℃，接近试验达到的最高温度446 ℃。从列车运行安全的角度考虑，本文计算结果更加接近车轮能够达到最高温度，更能反映车轮温升最严重的情况。因此，本文建立的车轮“运动-温度”有限元分析模型用于分析长大下坡道货运列车周期性制动对车轮温升的影响是可行的。

2 车轮温升数字实验案例及结果

本文以货运列车(2HXD2+50C70)为对象，对其在单一长大坡道上周期性制动进行计算。相关参数说明如下：闸瓦为高摩合成闸瓦，宽度为85 mm；列车总质量为4 900 t；坡道长度为15 km；外界空气温度和车轮初始温度均为40 ℃。周期性制动限速为1 400 m制动距离标准的紧急制动限速，按文献[16]公式计算；减压量为满足能使列车降速的最小减压量。

图5为列车在各坡度长大下坡道上周期性制动时车轮最高温度，计算结果表明，车轮最高温度与下坡道坡度值和电制动力失效的机车台数呈正相关关系。对于5 000 t级货运列车，采用周期性制动运行15 km的情境下，若2台机车电制动力均能正常发挥，车轮温度不超过350 ℃；若仅1台机车电制动力能发挥，坡度超过−23.7‰时车轮最高温度会超过400 ℃；若电制动力完全失效，坡道超过−12.5‰时车轮最高温度会超过400 ℃。

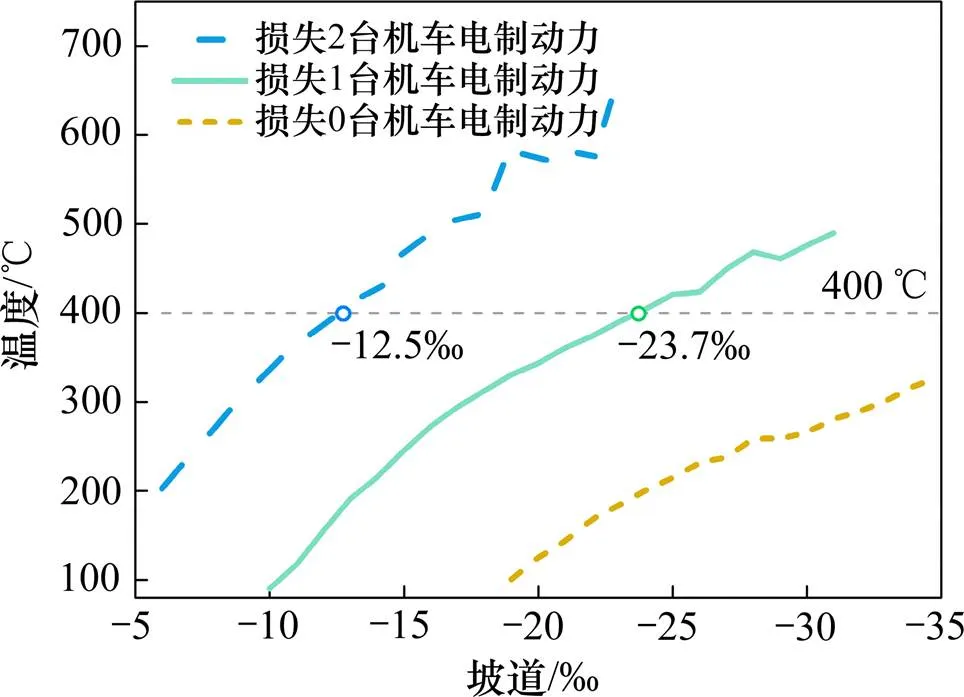
图5 车轮最高温度

列车周期性制动过程中，车轮最高温度随运行里程的变化情况如图6所示。车轮最高温度呈现出先上升后下降的周期性变化，这与列车运行速度变化规律相一致。列车抱闸制动过程中，运行速度降低，输入车轮的摩擦热相应减小，车轮温升速率降低；当速度降低至一定程度，对流耗散的热量超过输入车轮的摩擦热，车轮温度缓慢降低。列车缓解增速过程中，闸瓦离开踏面之初，踏面处与外界空气温差大，对流耗散热量大，车轮最高温度快速下降；随后降温过程缓慢，车轮温度无法在下一次抱闸前完全降到初始温度。因此，随着周期性制动次数的增加，车轮会达到的最高温度会不断升高，但会逐渐趋于稳定。

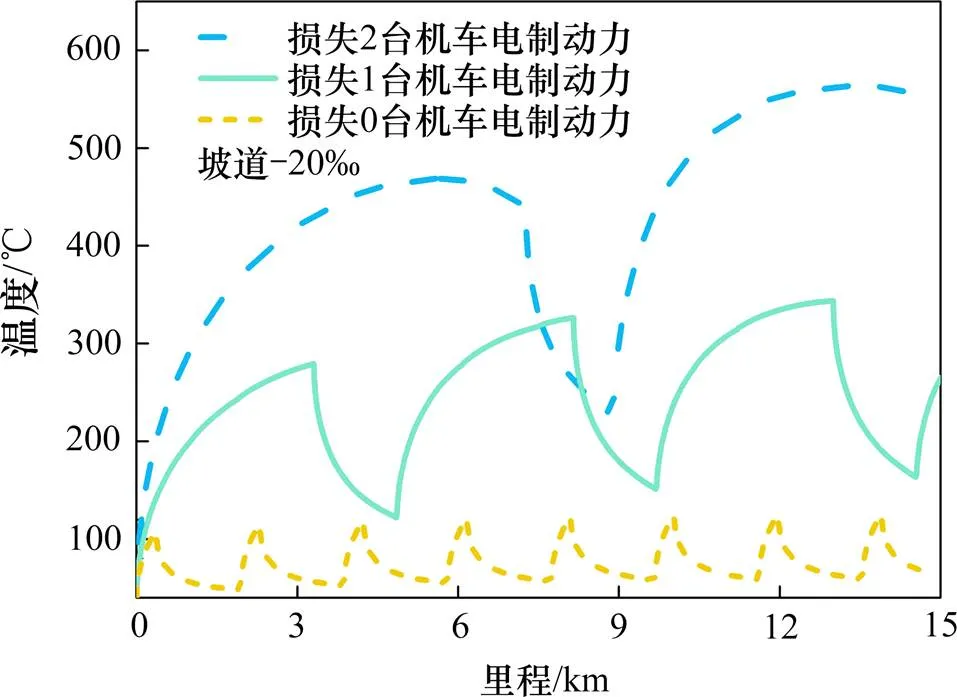
图6 车轮最高温度随制动过程的变化

3 周期性制动参数对车轮温升的影响

列车周期性制动主要受坡度、电制动力大小、减压量、制动限速和缓解速度的影响，但坡道、电制动力大小也是通过减压量和制动限速影响制动过程的，并且当制动限速确定后缓解速度也相应确定。因此，下文着重分析减压量和制动限速对车轮最高温度和温度变化过程的影响。

3.1 不同减压量

改变减压量，变化范围为60~170 kPa，步长为10 kPa；坡道为−20‰，发挥电制动力的机车数为1台，制动限速为91 km/h。如图7(a)所示，车轮最高温度与减压量呈正相关。减压量每增加10 kPa，温度平均增加13.6 ℃；当减压量达到97 kPa时，车轮最高温度会超过400 ℃。

以170 kPa和60 kPa为例，分析减压量对车轮温度随列车运行里程变化的影响，如图7(b)所示。减压量影响列车闸瓦压力和副风缸充风时间，从而影响车轮抱闸温升速率和缓解降温。当采用60 kPa减压量时，车轮抱闸温升速率为68.4 ℃/km；采用170 kPa减压量时，温升速度为589.1 ℃/km。这主要是由于：采用较大减压量时，列车抱闸时闸瓦压力大，使得列车更快减速的同时，输入车轮的摩擦热和热流密度更大。另外，采用170 kPa减压量时，缓解结束后车轮温度降至100 ℃左右，比60 kPa减压量约低40 ℃。原因主要在于：虽然采用大减压量抱闸结束后车轮温度更高，但较大减压量要求更长缓解增速时间以满足再充风，这使得在列车缓解过程中车轮降温更充分。

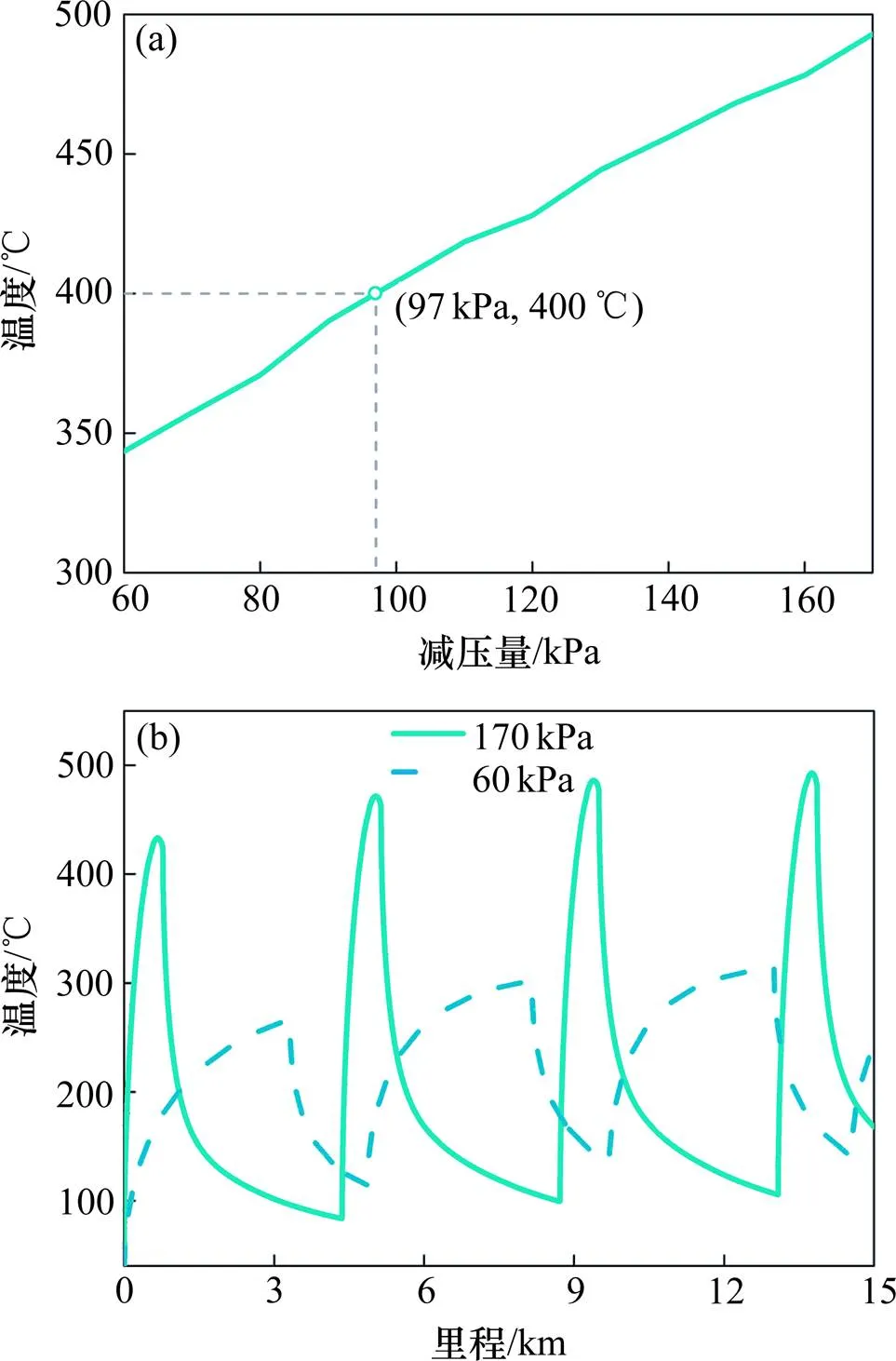
(a) 不同减压量；(b) 温度随里程变化

3.2 不同制动限速

改变制动限速，变化范围为50~91 km/h，步长为5 km/h；坡道为−20‰，发挥电制动力的机车数为1台，减压量为60 kPa。如表8(a)所示，车轮最高温度与限速呈正相关，限速每降低5 km/h，温度平均降低16.2 ℃；当限速降至86.5 km/h时，车轮温度不超过300 ℃。

以90 km/h和50 km/h为例，分析制动限速对车轮温度随列车运行里程变化的影响，如图8(b)所示。制动限速影响闸瓦摩擦系数和车轮制动功率，从而影响车轮温升速率、最高温度和温度变化周期。在15 km的范围内，按90 km/h限速运行时，车轮温度经历4个周期；按50 km/h限速运行时，车轮温度经历9个周期。从第一个温升周期看，90 km/h限速时列车运行3.178 km，车轮温度升至274.3 ℃；50 km/h限速时列车运行0.952 km，车轮温度升至140.4 ℃。原因主要在于：降低限速，平均闸瓦摩擦系数增大，列车减速更快，抱闸状态下列车运行距离更短，车轮温度周期性变化更加频繁；另外，低限速时由于列车平均运行速度低，车轮制动功率低，车轮达到的最高温度更低。

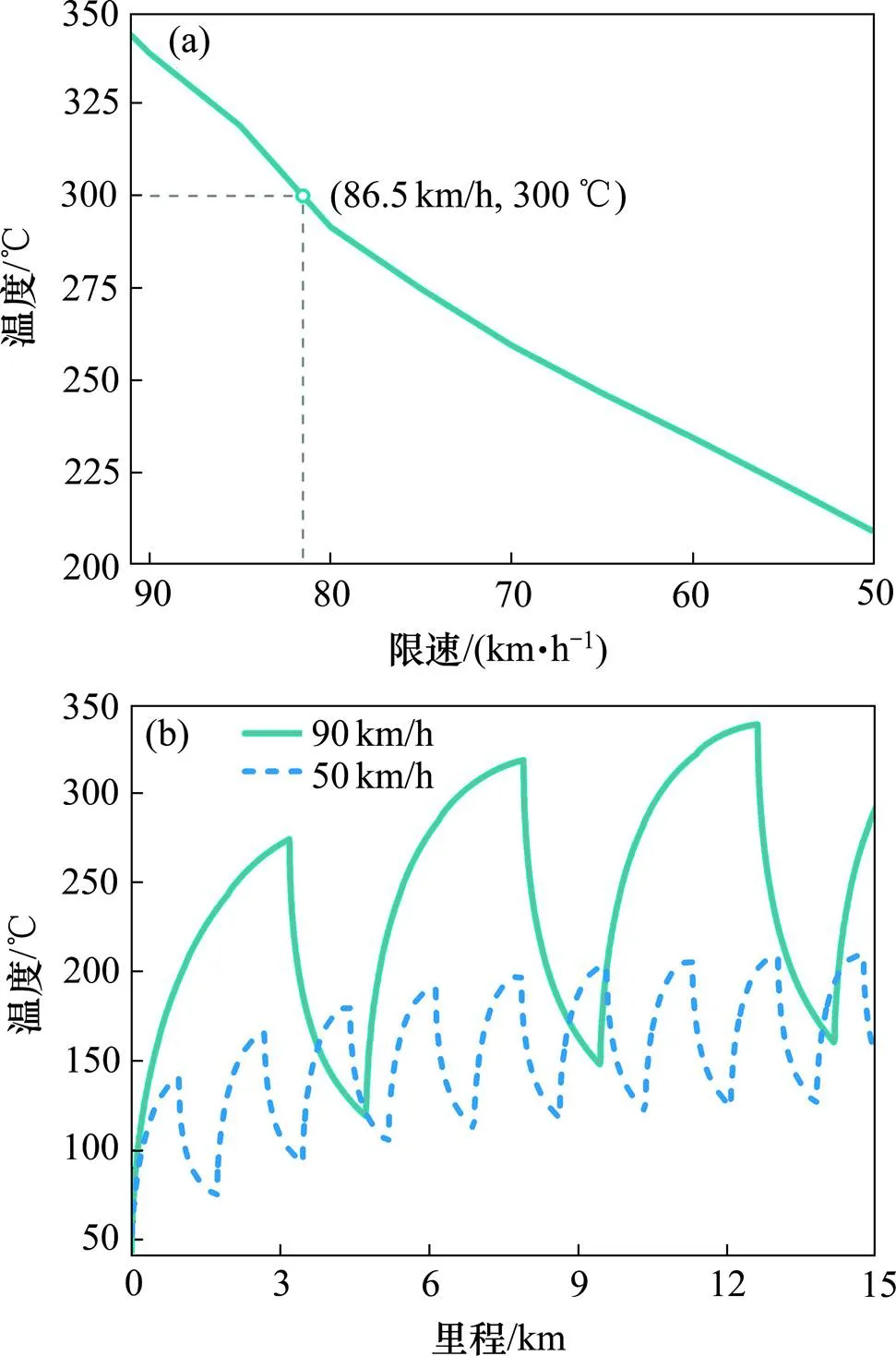
(a) 不同制动限速；(b) 温度随里程变化

4 结论

1) 提出了列车长大下坡道周期性制动下热流密度和对流系数的计算方法，利用ANSYS软件建立二维车轮“运动−温度”有限元分析模型，与已有研究实验数据的对比表明模型能够较好地反映车轮温升情况，验证了模型的有效性。

2) 车轮最高温度与坡道值和电制动力失效的机车台数呈正相关。HXD2双机牵引5 000 t级货运列车在15 km的下坡道运行，无电制动力损失时车轮温度不超过350 ℃；在1台机车电制动力损失和电制动力完全损失情况下，当坡道分别达到−23.7‰和−12.5‰后，车轮温度会超过400 ℃。

3) 车轮最高温度与周期性制动减压量、制动限速呈正相关。在设定前提下，不同减压量影响闸瓦压力和再充风时间，减压量每增加10 kPa，温度平均增加13.6 ℃；不同制动限速影响车轮制动功率和闸瓦摩擦因数，限速每降低5 km/h，温度平均降 低16.2 ℃。

4) 针对列车运营操纵的空气制动过程，可通过采用小减压量并适当降低运行限速来缓解车轮温升，提高行车安全。列车在长大下坡道进行制动操纵时，应尽量采用电制动力对车速加以控制。当电制动力不足而需要空气制动补偿时，宜采用较小的减压量并适当降低运行限速，以缓解车轮温度上升速率，降低车轮所达到的最高温度。

[1] 马大炜. 货车车轮热负荷的研究[J]. 铁道机车车辆, 1999, 19(5): 1−4. MA Dawei. Research on wheel heat load of freight car[J]. Railway Locomotive & Car, 1999, 19(5): 1−4.

[2] Teimourimanes S, Vernersso T, Lunden R, et al. Tread braking of railway wheels-temperatures generated by a metro train[J]. Proceedings of the Institution of Mechanical Engineers Part F—Journal of Rail and Rapid Transit, 2014, 228(2): 210−221.

[3] 彭莉, 谢基龙, 郑红霞. 大秦线全程制动条件下货车车轮温度及热应力场的数值模拟[J]. 北京交通大学学报, 2007, 31(1): 37−40. PENG Li, XIE Jilong, ZHENG Hongxia. Numerical simulation of temperature and thermal stress field of wagon wheel under Omnidistance Braking in Daqin Line[J]. Journal of Beijing Jiaotong University, 2007, 31(1): 37−40.

[4] 李兰, 蔡国武, 郭刚. 轮轨滚动接触和制动热负荷耦合作用对重载车轮踏面裂纹萌生寿命的影响[J]. 中国铁道科学, 2019, 40(3): 89−96. LI Lan, CAI Guowu, GUO Gang. Coupling effect of wheel-rail rolling contact and braking thermal load on crack initiation life of heavy haul wheel tread[J]. China Railway Science, 2019, 40(3): 89−96.

[5] 侯耐. 重载货车车轮踏面制动热负荷研究[D]. 成都: 西南交通大学, 2008. HOU Nai. Heat load analysis of heavy-haul freight car wheel for thread braking[D]. Chengdu: Southwest Jiaotong University, 2008.

[6] 张金煜, 虞大联, 林鹏. 基于旋转热源法和均布热源法的列车踏面制动温度场分析[J]. 机械工程学报, 2018, 54(6): 93−101. ZHANG Jinyu, YU Dalian, LIN Peng. Analysis of temperature field of train tread braking based on rotating heat source method and uniformly distributed heat source method[J]. Journal of Mechanical Engineering, 2018, 54(6): 93−101.

[7] 应之丁, 李小宁, 林建平, 等. 列车车轮踏面制动温度循环试验与温度场仿真分析[J]. 中国铁道科学, 2010, 31(3): 70−75. YING Zhiding, LI Xiaoning, LIN Jianping, et al. The temperature cycle test of wheel tread braking for freight trains and the simulation analysis of the temperature field[J]. China Railway Science, 2010, 31(3): 70−75.

[8] 张乐乐, 杨强, 谭南林, 等. 基于摩擦功率法的列车制动盘瞬态温度场分析[J]. 中国铁道科学, 2010, 31(1): 99−104. ZHANG Lele, YANG Qiang, TAN Nanlin, et al. Analysis of the transient temperature field of train brake discs based on friction power method[J]. China Railway Science, 2010, 31(1): 99−104.

[9] 文永蓬, 周伟浩, 徐小峻, 等. 考虑热力耦合的轨道车轮辐板参数优化研究[J]. 铁道科学与工程学报, 2016, 13(10): 2042−2050. WEN Yongpeng, ZHOU Weihao, XU Xiaojun, et al. Study on parameter optimization for the rail wheel considering thermal-mechanical coupling[J]. Journal of Railway Science and Engineering, 2016, 13(10): 2042− 2050.

[10] Walia M S, Esmaeili A, Vernersson T, et al. Thermomechanical capacity of wheel treads at stop braking — A parametric study[J]. International Journal of Fatigue, 2018, 113: 407−415.

[11] Ertz M, Knothe K. A comparison of analytical and numerical methods for the calculation of temperatures in wheel or rail contact[J]. Wear, 2002, 253: 498−508.

[12] 文永蓬, 徐小峻, 尚慧琳, 等. 考虑热力耦合的轨道车辆车轮建模与仿真[J]. 交通运输工程学报, 2016, 16(5): 30−41. WEN Yongpeng, XU Xiaojun, SHANG Huilin, et al. Modeling and simulation of railway vehicle wheel considering thermo-mechanical coupling[J]. Journal of Traffic and Transportation Engineering, 2016, 16(5): 30− 41.

[13] 李金良, 肖楠, 谢基龙. 重载货车车轮踏面制动辐板热应力分析[J]. 机械工程学报, 2012, 48(12): 133−138. LI Jinliang, XIAO Nan, XIE Jilong. Thermal stress analysis of the heavy-haul freight car’s wheel web plate under the wheel tread braking[J]. Journal of Mechanical Engineering, 2012, 48(12): 133−138.

[14] 李兰, 常崇义. 基于热—机耦合的大轴重车轮踏面制动热负荷仿真分析[J]. 铁道机车车辆, 2014, 34(2): 25−30. LI Lan, CHANG Chongyi. Thermal load analysis of wheel tread for heavy axle load freight car under braking conditions on the basic of thermal-mechanical coupling model[J]. Railway Locomotive & Car, 2014, 34(2): 25− 30.

[15] TB/T 1407.1—2018, 列车牵引计算[S].TB/T 1407.1—2018, Railway train traction calculation[S].

[16] 刘海东, 苏梅, 彭宏勤, 等. 城市轨道交通列车制动问题研究[J]. 交通运输系统工程与信息, 2011, 11(6): 93− 97. LIU Haidong, SU Mei, PENG Hongqin, et al. Braking performances of urban rail trains[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(6): 93−97.

Analisis of wheel temperature rise of freight trains on long ramp under periodic braking

MAO Baohua1, 2, GONG Chaoqi1, ZHANG Tong1, YANG Yanqiang1

(1. Key Laboratory of Transport Industry of Big Data Application Technologies for Comprehensive Transport,Beijing Jiaotong University, Beijing 100044, China; 2. Integrated Transportation Research Centre of China, Beijing Jiaotong University, Beijing 100044, China)

Periodic braking is a common operational strategy for freight trains running on the long downhill ramp, during which wheel temperature will rise due to frequent air braking, and the excessive temperature can endanger the driving safety. In order to improve the safety of train operation, considering the effect of periodic braking on heat flow density and convective heat transfer coefficient, this paper establishes a two-dimensional wheel “movement-temperature” finite element analysis model based on ANSYS software. Compared with the existing experiment results, the model is verified by carrying out numerical experiments. Under the premise of the paper’s setting, the results show that: the wheel temperature will not exceed 350 ℃ with no electric braking force loss and the wheel temperature will exceed 400 ℃ when the ramp exceeds −23.7‰ and −12.5‰ respectively for half and complete electric braking power loss. When the pressure reduction increases by 10 kPa, the maximum temperature of the wheel goes up by 13.6 ℃ on average, and while the braking speed limit decreases by 5 km/h, the maximum temperature of the wheel goes down by 16.2 ℃ averagely. The results can provide reference for the route design of ramp and the operation organization after electric braking failure.

freight trains; periodic braking; wheel temperature rise; train pipe pressure reduction; braking speed limit

U270

A

1672 − 7029(2020)04 − 0980 − 08

10.19713/j.cnki.43−1423/u.T20190647

2019−07−17

国家自然科学基金资助项目(71971021)

毛保华(1963−)，男，湖南祁阳人，教授，博士，从事城市轨道交通、运输组织理论与方法及综合交通发展理论研究；E−mail: bhmao@bjtu.edu.cn

(编辑 蒋学东)