高中数学几何问题探究

刘建国

(保定市顺平县职业技术教育中心 河北 顺平 072200)

数学知识变化莫测，使得数学世界变得丰富多彩。就如简单的两条直线就有平行、重合、共面、异面等多种关系，简单的一条线、一个面也可以组成多种位置关系。课时学生对于几何类问题的解答，受到自身空间想象能力和逻辑思维能力多种能力的影响。因此，为了培养学生的这些几何能力，对高中几何几种题型进行了分析探讨。

1.利用几何图形的平行、垂直位置关系解决立体几何问题

通常情况下，几何图形的平行问题主要分为线与线之间的平行关系、线与面之间的平行关系和面和面之间的平行关系几种问题。解决这三类问题通常会用到平行公理、线面平行性质定理、线面垂直性质定理和线面平行性质定理几块知识内容。其中判断线面平行问题是，最常使用的方法就是线面平行定理。然而如何在一个平面中找到一条直线的平行线是学生倍感苦恼的问题，需要我们教师加以引导，让他们学会用性质定理分析问题、解决问题。另外三垂线定理和逆定理在解决几何位置关系中，发挥了重要的作用，在高中中出现的频率也相对较高。添加辅助线是培养学生利用已知条件探索解决问题办法的有效途径之一，也是学生需要掌握以及熟练运用的。

2.立体几何空间角解题技巧

立体几何里面空间角的问题是高考必考内容，所以说对这块内容的学习是重点。空间角分成异面直线所成角、直线与平面所成角、二面角几种形式。利用定义求空间角也常用方法，既利用空间角的定理来寻找空间几何体的结构特征，从而顺利将空间角转换成平面角，把立体几何转变到平面几何问题上来，有效降低了解题难度。其关键点在：第一根据空间角的定义来找到角。找角主要是在已经知道的空间角上添加辅助线找出空间角里的平面角。第二证角。我们找到角以后还要证明这个角就是题目中要求的角。第三步求角。把找到的角放在平面中，然后再利用定理来求角。

空间角的问题通常线面角出题率较高，我们可以利用传统方法解答此类问题。如下题：

证明：∵地面ABCD为矩形，又∵AD垂直于PD。CD与PD相交于D点，∴AD与平面PCD垂直，而AD属于底面，所以底面和平面PDC也垂直。

对于异面直线所成的角这类问题，解题的关键所在就是利用几何定义找到解题突破点，异面直线所构成的角，从定义我们知道这个角就是由空间中任意一点到两个异面直线的平行线构成的，那么从空间中所取的这个点就是解题的突破点。一般情况下我们选择一条线段的端点或中点、等分点。如下题：

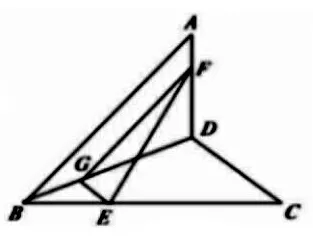
那么，解答此题的时候，我就把B点和D点连接起来，取了上面一个点G，使得BG:GD=A:2.这样就找到了题目的突破口。

3.立体几何中空间距离的计算方法

在高中立体几何中，空间距离主要涉及到点到直线的距离、异面直线间的距离、点到平面的距离三个方面。对于求点到直线距离的问题，我们通常采用三垂线定理得到三角形来求解，另外还可以利用面积相等的原理来求解；对于异面直线间空间距离问题，可以找出两条异面直线的公垂线，转换到线段长度问题上来；对于点到平面距离的问题，通常是从这点出发，做平面的垂线。也可以利用“三棱锥体积法”来解决此类问题，然而在我们直接接找点到平面垂线比较困难的时候，就从点所在直线中，找到另外一点到平面的距离，这样就可以把点到平面的距离求解转移到直线到平面距离问题上来进行求解。

4.平面图形翻折与立体图形展开问题技巧

平面图形经过翻折或者我们在解题过程中把立体图形展开解题是立体几何解题常用方法，也是高考常考的热点问题，需要我们教师长期地引导学生熟练掌握此解题方法。我们在解题时沿着某一条直线，把平面图形翻折得到一个立体图形，那么这条直线其实就是图形旋转的一个轴。对于此类问题的解答，首先要弄清变化了的量和位置关系，找到变化的内容和没有变化的内容，然后把没有变化的条件集中起来，都在立体图形中进行分析，这样就把条件和问题结合成为一个比较明朗的立体几何问题。

立体几何解题时，把立体几何问题转变成平面几何问题，能够有效降低难度，使得学生思维顺利进行迁移。把立题几何展开以后，得到一个平面图形，然后弄清楚立体几何中相关点、面在展开后的关系，这就是解决展开立体几何问题的突破点。如下题：

求上图长方体中，一个蜘蛛从从A点到B点的最短距离是多少。那么此问题就可以把立体图形展开，把表面积的位移问题转化成平面里的位移问题。

总之，在高中几何问题的学习中，需要教师采用科学的手段，帮助学生学习有效解决问题的方法，使得他们的立体空间想象能力得到提升。同时也培养学生发散思维，使他们能够顺利进行问题的转换，降低解题难度，使学生在高考中能够顺利找到问题的突破点，快速解决问题。