基于排错等待延迟的广义动态集成神经网络模型*

惠子青,刘晓燕,严 馨

(昆明理工大学信息工程与自动化学院，云南 昆明 650500)

1 引言

随着计算机技术的高速发展，软件系统的规模和复杂度在不断上升，并因其在航天、医疗、军事等安全关键领域的广泛应用，使得计算机软件的可靠性和安全性对人们变得非常重要。软件系统失效不仅会导致重大的经济损失，严重时还可危及社会和人身安全，因此如何保障软件系统的可靠性成为近年来软件工程的研究热点之一。

为了能够准确评估软件的可靠性，现已开发出上百种应用于实际项目的软件可靠性增长模型SRGMs(Software Reliability Growth Models)[1]。软件可靠性增长模型主要分为2类：第1类是带参数模型，如传统的G-O模型[2]、Pham模型[3]、Yamada-TEF[4]等。这些模型相对理想化，且模型的通用性和预测精度不高。第2类是无参数模型，如动态加权组合模型DWCM(Dynamic Weighted Combinational Model)[5]、广义动态集成模型GDIM(Generalized Dynamic Integrated Model)[6]、基于测试效率的神经网络结构TE-ANN(Testing Efficiency Based Neural Network Architecture)[6]等。近年来人工神经网络ANN(Artificial Neural Networks)仿真的出现，为软件可靠性评估和预测提供了一条新途径。由于神经网络仅需要将历史故障数据作为输入且不需要任何假设条件，因此相比传统的软件可靠性模型神经网络模型具有显著优势。人工神经网络为软件可靠性评估和预测提供了非常有效的解决方案。Karunanithi 等[7,8]首先提出神经网络模型可应用于软件可靠性增长预测和不同复杂度模型的开发。Khoshgoftaar等[9,10]介绍了静态可靠性建模的方法，其使用神经网络结构预测软件中的故障数量。Sherer[11]使用神经网络有效预测了NASA项目中的软件故障。Khoshgoftaar等[12]比较了“神经网络”和“参数化模型”软件可靠性预测的方法和性能。Cai 等[13]发现了输入层和隐藏层神经元数量以及隐藏层数量对网络结构的影响。Su 等[14]从软件可靠性建模的数学角度解释了神经网络，并通过设计网络结构的不同元素将神经网络应用于传统的软件可靠性建模。魏霖静等[15]提出了一种基于Logistic增长的神经网络测试方法。由于上述提到的神经网络方法均假设故障被检测出以后被立即排除，这个假设与实际情况并不相符。在实际测试中，故障排错等待延迟是不可忽略的，因此如何考虑故障排错等待延迟问题，建立更加贴近实际测试过程的神经网络模型，是目前工作的研究方向。

为了更加准确地描述软件故障修正的过程，本文针对故障排错等待延迟现象，提出了一种考虑故障排错等待延迟的神经网络模型RWD-SRGM(Removal Waiting Delay Software Reliability Growth Model)。该模型综合考虑软件工程的多样性，利用神经网络的方法构建广义动态集成网络模型，并结合故障排错等待延迟现象完成故障的检测和预测。本文其余部分安排如下：第2节简要介绍了神经网络的基本概念以及ANN的建模机理；第3节介绍了排错等待延迟的概念和考虑排错等待延迟的广义动态集成神经网络模型；第4节介绍了参数估计的方法和实验结果分析；第5节是总结与展望。

2 预备知识

2.1 神经网络概述

ANN是受生物神经系统行为启发而出现的一种非线性、自适应的信息处理系统[16]。ANN通过构造大量高度互联的神经元，使它们协同工作，用于处理和解决复杂全局行为的特定问题。神经网络模型由3个部分组成[17]：神经元、拓扑结构和学习算法。

(1)神经元：是一种有多个输入或输出的装置，具有接收输入信号、处理信号和产生输出信号的功能。神经元的数学模型如图1所示。

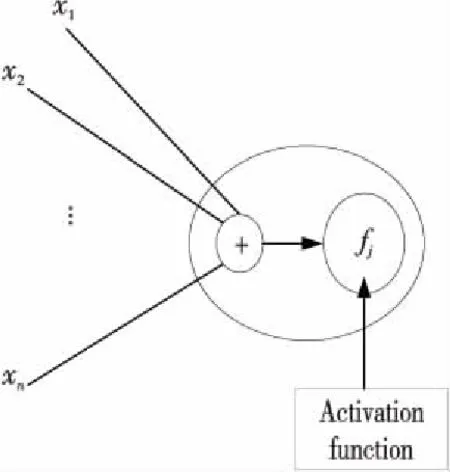
Figure 1 Mathematical model of neuron图1 神经元的数学模型

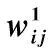
Figure 2 A multilayer feedforward neural network图2 多层前馈神经网络

(3)学习算法：描述了一个动态调整权值的过程，在学习阶段，各神经元进行规则学习，权参数调整，再通过非线性映射关系拟合以达到训练精度；判断阶段则是利用训练好的稳定网络读取输入信息，通过计算得到更好的近似输出结果。

2.2 ANN的建模机理-以G-O模型为例

首先用简单前馈神经网络结构的S_SRGM(Simple SRGM)来说明神经网络方法与传统的SRGM的映射关系。S_SRGM由1个神经元组成,其包括输入层、隐藏层和输出层，如图3所示。

Figure 3 Feed-forward network with single neuron in each layer图3 单神经元前馈网络图

在基于非齐次泊松过程NHPP(Non-Homogeneous Poisson Process)的故障检测模式中，累计故障次数N(t)通过强度函数λ(t)和累计故障数的期望值m(t)=E(N(t))来定义。m(t)通过式(1)得出：

(1)

基于NHPP的模型都是假设在(t,t+Δt)内检测出的故障总数与软件中剩余故障的数量呈正比，由以下微分方程表示：

(2)

其中,b(t)为故障检测率函数，a(t)为故障总数函数。

单神经元前馈网络模型和传统NHPP模型之间的映射关系如下所示：

(1)β(t)相当于SRGM的均值函数m(t)。

(2)w1是软件失效率。

(3)w2是故障检测率。

(4)隐藏层中α(x)的输出相当于分布函数。

例如，如果在隐藏层中构造1个具有激活函数α(i)=1-e-i的神经网络，在输出层中构造1个线性激活函数β(i)=i，并且在隐藏和输出中没有偏置。那么，权重为w1的隐藏层输入为：

x(t)=w1t+b1

(3)

其中,b1是偏置。

隐藏层的输出可以表示为：

h(t)=α(x(t))=1-e-x(t)

(4)

如果偏置b1可以忽略，本文假设其为零，那么隐藏层的输出为：

h(t)=1-e-w1t

(5)

现在输出层的输入是：

y(t)=h(t)w2+b0

(6)

如果偏置b0可以忽略，假设其为零，则输出层的输出为：

g(t)=β(y(t))=w2(1-e-w1t)

(7)

式(7)就是用神经网络方法构建的G-O模型。如果假设w1=b，w2=a，则式(7)与传统的G-O模型相对应。使用神经网络对传统SRGM建模的步骤如图4所示。

Figure 4 Steps for SRGM to construct a neural network图4 SRGM构建神经网络的步骤

故障排错等待延迟是软件测试工作中不可忽略的一个重要问题。现有的神经网络模型一般不考虑排错等待延迟时间，或者认为其故障排错等待时间为一个常数值，这是非常不切合实际的。

3 考虑排错等待延迟的GDIM

Figure 5 Timeline of fault detection & correction图5 故障检测与修正时间轴

3.1 故障排错等待延迟的概念

定义1 故障排错等待延迟RWD(Removal Waiting Delay)指故障被检测后，等待故障修正人员开始进行故障重现、故障诊断和代码修改之前的时间段[18]。

在实际的测试过程中，故障的复杂度不同，修正所需要的资源和时间也不同，我们首先给出软件故障影响严重性级别，Defamie等[19]给出了西门子公司的故障级别严重性分类方法，如表1所示。

Table 1 Software failure severity level表1 软件故障严重等级

Gokhale等[20]把软件系统中的故障分为了m种类型，从m～1软件故障的严重级别依次增大，即1的严重级别是最高的，m的严重级别是最低的。根据M/M/1排队模型，假设软件失效故障服从参数为λ的泊松过程，软件故障检测时间服从参数为μ的指数分布。严重级别为j的缺陷被分配给每个维修人员的比率表示为:

(8)

其中,N表示软件测试人员的个数。

对于严重级别为j的缺陷，每个维修人员的利用率表示为:

(9)

缺陷维修可采用2种策略：非抢占式优先权和抢占式优先权。本文采用非抢占式优先权，其工作流程为：级别越高的故障排队越靠前，正在维修的故障不受排队故障故障级别的影响，如正在维修低级别的故障，虽然高级别的故障到达队列，但只有低级别维修故障结束后才能开始高级别故障的维修。因此，严重级别为j的故障，其平均维修时间tj可以表示为：

(10)

3.2 考虑排错等待延迟的GDIM推导

3.1节详细叙述了故障排错等待延迟的概念以及故障平均维修时间tj的推导过程，在本节将具体介绍关于考虑排错等待延迟的神经网络模型的建立过程。

3.2.1 提出模型的假设条件

(1)软件故障检测时间服从指数分布。

(2)任意时刻软件故障是由软件中存在的故障引起的。

(3)软件故障之间相互独立。

(4)在软件测试周期，软件修正的故障数量一直小于被检测的故障数量。

(5)软件系统产生的每个故障都会被修正，且修正过程和检测过程互不影响。

(6)GDIM中隐藏层的第1个单元和输出层的每个单元中没有偏差，且隐藏层中的其他神经元都具有偏差cj-1(j=2,…,n)。

3.2.2 一般的GDIM模型

广义动态集成模型GDIM[6]是一种使用软件故障复杂度的集成模型，定义任何软件都可以包含n种不同类型的软件故障，且每个故障的排除策略不一样，其故障类型可依据延迟时间来区分。如果故障检测、定位和排除之间的时间延迟忽略不计，则称其为简单故障；如果检测和定位之间存在时间延迟，则称其为困难故障；如果故障检测、定位和排除之间存在时间延迟，则称其为复杂故障。

本文研究包含3种故障类型的GDIM，这种类型的神经网络在输入和输出层中有1个神经元，在单个隐藏层中有3个神经元，如图6所示。

Figure 6 3 layer network structure of GDIM图6 广义动态集成模型的3层网络结构

隐藏层中3个神经元的激活函数是：

α1(x)=1-e-x

(11)

(12)

(13)

输出层单神经元的输出是：

g(t)=w21(1-e-w11t)+

(14)

如果将式(14)中权重w1j用第i类故障的故障检测率bj(j=1,…,n)替换，权重w2j用系统中未被检测出的第i类故障的总数aj(j=1,…,n)来替换，则具有3种类型故障的神经网络的均值函数可以表示为：

m(t)=g(t)=a1(1-e-b1t)+

(15)

其中γj=cj-1,j=2,…,n。

3.2.3 考虑排错等待延迟的GDIM

根据假设条件，本文将故障平均维修时间tj引入到GDIM中，并将考虑排错等待延迟的广义动态集成神经网络模型命名为RWD-SRGM，其均值函数m(t+tj)可以表示为：

m(t+tj)=a1(1-e-b1(t+tj))+

(16)

4 实验与分析

为了充分、有效地评价RWD-SRGM的拟合性能和预测性能，本文还选取了Logistic增长曲线模型[15]进行仿真实验与分析。表2给出了本文中提到的所有软件可靠性增长模型。

4.1 模型的评价指标

为了验证RWD-SRGM的性能，分别采用了3种不同的的评价准则[21],对模型拟合结果进行评价，分别为均方平方误差MSE(Mean Square Error)、确定系数R-square(Coefficient of determination)和相对误差RE(Relative Error),如式(17)～式(19)所示。

(17)

其中,mc(ti)和m(ti)为实际失效故障数据和预测失效故障数据。MSE的值越小，表明模型的拟合性能越好。该MSE仅用于比较不同模型在同一数据集上的应用效果。

(18)

(19)

其中,mc(ti)和m(ti)分别为实际失效故障数据和预测失效故障数据。RE曲线越靠近x轴，模型拟合故障数据的能力越好。

为了验证RWD-SRGM的性能，首先需要应用极大似然估计法进行模型的参数估计。本文所提到的4种模型参数估计值如表3所示，其中GDIM和tj共同提供了RWD-SRGM的最优参数估计值。

Table 2 Summary of some SRGMs and their m(t)表2 软件可靠性增长模型和m(t)

Table 3 Model/parameter estimation表3 模型/参数估计值

4.2 实验结果分析

本文采用了实时指令系统故障数据集(DS1)[22]和IBM入门开发软件包故障数据集(DS2)[23]2组失效数据集，对RWD-SRGM进行了统计学分析和模型拟合度分析，2个失效数据集的测试周期分别为25周和12周。表4给出了各模型在2组失效数据集上的拟合结果。

Table 4 Comparison of simulation results with different models表4 不同模型的拟合结果对比

由表4可见，在使用实时指令系统故障数据集(DS1)仿真时,与其它模型对比可以看出：(1)RWD-SRGM的MSE值最小,为18.32；其次是Logistic-SRGM,为23.58；最差是传统G-O模型，为28.26；(2)RWD-SRGM的R-square值为0.986 1，最接近1；其次是Logistic-SRGM,为0.975 2；最差是传统G-O模型，为0.952 6。

图7显示了各模型对于DS1数据集的最佳拟合曲线对比图。显而易见，RWD-SRGM的拟合曲线比其它3种模型的拟合曲线更优，次优的模型是Logistic-SRGM，其原因可以解释为总故障数a(t)随时间基本满足指数增加的事实；排名第3的模型是GDIM；性能最差的模型是传统G-O模型，其原因可以解释为，虽然传统G-O模型是最经典的模型，但由于其假设a(t)和b(t)为常量，使得其性能是4种模型里面最差的。这与图7中传统G-O模型的拟合曲线偏离真实失效数据集的程度相符合。

图8显示了4种SRGM在DS1数据集上的RE对比曲线。显然RWD-SRGM的RE下降最快，趋近于x轴；次优的模型是Logistic-SRGM；排名第3的模型是GDIM；性能最差的是传统G-O模型，它在前期严重地偏离了x轴。其余3个模型预测结果基本相同，尤其在t=15时曲线开始向x轴无限逼近。

Figure 7 Four fitting curves on the DS1 dataset图7 DS1数据集上的4种拟合曲线

Figure 8 RE results on the DS1 dataset图8 DS1数据集上的RE结果

由表4可见，在使用IBM入门开发软件包故障数据集(DS2)进行仿真实验时,与其它模型对比可以看出：(1)RWD-SRGM的MSE值最小，为5.89；其次是GDIM，为8.22；最差是传统G-O模型，为12.75。(2)RWD-SRGM的R-square值为0.977 2，最接近1；其次是GDIM,为0.968 2；最差是传统G-O模型，为0.965 8。

图9显示了各模型对于DS2数据集的最佳拟合曲线对比图。显而易见，RWD-SRGM的拟合曲线比其它3种模型的拟合曲线更优，次优的是模型GDIM，排名第3的是Logistic-SRGM，性能最差的是传统G-O模型。由图9可以看出，4个模型的拟合效果差别并不大，其原因可以解释为当数据集较小时，神经网络无法充分训练，导致其拟合性能和预测性能与传统G-O模型的差异性并不明显。

Figure 9 Four fitting curves on the DS2 dataset图9 DS2数据集上的4种拟合曲线

图10显示了4种SRGM在DS2数据集上的RE对比曲线，显然RWD-SRGM的RE下降最快，趋近于x轴，次优的是GDIM模型，排名第3是Logistic-SRGM，性能最差的是传统G-O模型。RE曲线在t=8时，开始逐渐收敛于x轴，呈现加强的趋势。这是因为在3/4测试时间以后，测试环境和技术开始趋于稳定状态，使得模型的拟合和预测性能开始变好。

Figure 10 RE results on the DS2 dataset图10 DS2数据集上的RE结果

2组故障数据集上的实验结果表明：Logistic-SRGM在DS1上的拟合性能较好，但在DS2数据集上的拟合偏差较大，这说明一个模型不可能适用于所有的数据集。由于测试人员对测试过程认知的差异，以及所使用的模型、参数估计方法的不同，使得各模型在不同数据集上的性能差别较大。但总体来说，本文所提出的RWD-SRGM，在DS1和DS2 2组数据集上都表现出了良好的拟合性能和模型通用性

5 结束语

本文针对软件测试过程中的排错等待延迟问题，提出了一种考虑排错等待延迟的神经网络模型RWD-SRGM，其在DS1和DS2 2组数据集上都显示出最优的拟合效果。由于所提模型的可靠性评估指标显著高于其它模型的，从而证明了RWD-SRGM在软件可靠性预测方面具有更高的预测精度和更好地模型适用性。RWD-SRGM相较于其它模型具有以下优势：(1)对故障数据集的拟合效果更优。(2)结合了故障排错等待时间，解决了在故障检测过程排错等待延迟问题，更好地贴近了实际。(3)在均方平方误差、确定系数、相对误差3个评价指标上均表现出更高的性能，即可靠性更高。

未来的研究方向表明，如何考虑更多真实的测试环境要素，建立通用性更高、预测精度更准确的软件可靠性增长模型，已成为当前研究中亟待解决的问题。具体来说，我们将进一步深入研究故障检测、故障排除、故障引进、排错等待延迟等影响软件可靠性评估精度的重要因素。与此同时，我们将结合其实际应用进行分析，例如测试资源管控、软件最优发布时间等问题，更好地将理论与实际应用结合起来。