C-Canny算法和改进单层神经网络相结合的面部特征点定位*

付文博，何 欣，于俊洋

(1.河南大学软件学院,河南 开封 475000；2.河南省智能数据处理工程研究中心,河南 开封 475000)

1 引言

面部多特征点定位是计算机视觉领域的重要问题，许多任务都依赖于面部特征点定位的结果，如面部表情分析、面部识别等。虽然面部特征点定位在近几年来被广泛研究，并且取得了巨大的成功，但是在处理复杂环境中的定位问题时(Semantic ambiguity)[1]，由于受到各种干扰因素的影响，图像具有复杂多样性，因此面部特征点定位仍面临巨大的挑战。卷积神经网络CNN(Convolutional Neural Netowrk)已被证实是一种可行的解决方案，CNN通过对面部图像进行旋转、平移、缩放，使得模型对姿态旋转更具鲁棒性。然而，在处理遮挡、光线不足等面部轮廓难以区分的图像时[2,3]，因其无法识别面部区域，CNN表现却不好。为解决上述问题，本文设计了一种单层VGG(Visual Geometry Group)神经网络[4 - 7]与Canny算法相结合的网络结构，能够在预测阶段对面部区域进行重定位，在消除面部噪声区域干扰的同时，提升特征点定位的准确性，在ibug提供的300-w[5]与300-vw[6]开源数据集上取得了较好的预测结果。

2 相关研究

面部特征点定位大致分为2个方向：传统方法与深度学习的方法。其中，典型的传统方法包括基于模型的方法和基于回归的方法。

2.1 基于传统方法(ASM、AAM，ERT,LBF)

基于传统方法的面部特征点定位主要分为基于模型的方法与基于回归的方法2类。其中，基于模型的方法主要是由Le等[8]提出的ASM(Active Appearance Model)、AAM(Active Appearance Model)模型。该模型对人脸、手、心脏等几何形状的物体，通过若干关键特征点的坐标依次串联，形成1个形状向量进行后期预测。然而ASM和AAM也存在一些不足，如处理多样性较强的面部表情时，单一的线性模型难以拟合现实场景数据中的复杂非线性变化，使得这类基于模型的方法鲁棒性较差。基于回归的方法主要是由Kazemi等[9]提出的基于ERT(Ensemble of Regression Trees)回归方法下的面部特征点定位，目前DLIB框架使用的正是此方法。这种方法通过建立残差回归树来使人脸形状从初始随机定位点集逐步回归到真实形状，并通过各关键点附近的随机森林来学习，最终得出LBF(Local Binary Feature)特征。虽然这种基于回归的方法能够有效定位特征点，但是判定结果的准确性高度依赖于前期的人工初始化定位工作。

2.2 基于深度学习的方法

在深度学习方式下的面部特征点定位，目前聚焦于基于2D卷积核下的神经网络结构设计与基于3D卷积核下的神经网络结构设计。基于2D卷积核的神经网络结构，典型的有由Liu等[1]提出的基于VGG神经网络结构与Sun等[2]提出的Cascade级联神经网络结构。这类基于2D卷积核的网络结构可以定位多角度下的面部特征点，但是在处理有遮挡、像素不高的图像时，定位结果较差。基于3D卷积核的神经网络结构，典型的有由Sagonas等[5]提出的3DMM(3D Morphable Models)网络结构，该网络结构对2D面部图像进行3D建模，并将3D空间的坐标轴分别定义为XT、YT和ZT，通过学习图像中的非可见面部信息，提升特征点定位的准确性。但是，这种3DMM网络结构遭到Tran等[10]的质疑：当图像向高维度转换时，图像会大概率地出现病态变异。虽然3D卷积的准确性已得到了业界认可，但是过高的病态图像比例也会大幅降低网络的预测效率。

由此可得，上述几种神经网络在面部特征点定位方面都有着可改进的空间。因此，本文设计了一种基于2D卷积核的单层神经网络结构，该结构经过大量的训练与调参，在面部特征点定位方面与上述一些基于深度学习的网络模型[1,3,4]相比有了较大的提升。

3 网络设计与面部特征点定位

3.1 网络设计

本文设计的神经网络除输入输出层之外还包含7个卷积层、4个池化层和1个全连接层，在1次或2次卷积操作以后紧跟1个池化层进行特征提取。本文设计的CNN结构参数如表1所示，结构图如图1所示。

Table 1 Neural network parameter表1 神经网络结构参数

Figure 1 Convolutional neural network structure in this paper图1 本文CNN结构图

本文神经网络输入层的参数是(128,128,3)的彩色图像以及与之相对应的面部特征点坐标集合，其中每一幅图像中包含68个面部特征点。为方便网络分批次迭代训练，需对每一幅图像中对应的68个特征点坐标(x,y)进行一元展开合并处理，变为(x1,y1,…,x68,y68)这样的格式类型。网络层数的确定参考了Cascade神经网络模型[7]，该模型采用双层网络结构，其目的是进行人脸相似度判断。而本文研究的是面部特征点定位，因此在原有网络模型的基础上进行改进，设计出一种基于单层VGG-16的神经网络结构[4]。其卷积输出的计算方法如式(1)所示：

N=(W-F+2P)/S+1

(1)

其中，N为输出图像的维度，W为每一层图像的输入维度，F为卷积核参数，S为步长，P为扩充的边缘像素数。每一次卷积计算以后结合ReLU激活单元进行输出：

ReLU=Max(0,wTx+b)

(2)

其中，w是神经元的权重值，x是图像，b是偏移量。输入的图像信息经过每层卷积、池化计算后，其维度会相应减小。本文选取ReLU激活单元对每层输出值进行极大值保留,从而使得神经网络在后续的训练过程中可以正常更新参数，并避免梯度消失。最终，在训练结束后可获得局部最优解。

3.2 数据归一化处理

ibug网站所提供的300-w与300-vw数据集中，每一帧图像都有对应的pts文本。该文本记录了面部特征点的坐标。利用这些面部特征点集合，可以定位图像中的面部矩形区域。其面部区域的左上角与右下角坐标的计算方法如式(3)所示：

(x1,y1)∈(min(x),min(y))

(x2,y2)∈(max(x),max(y))

(3)

其中,xi和yi分别为面部68个特征点对应的横坐标和纵坐标：

(xi,yi)={(x1,y1),…,(xm,ym)}

(4)

m为图像中特征点的样本总数，max和min分别代表求集合内的最大值和最小值。

为了避免神经网络在训练过程中出现过拟合的现象(overfit)，本文又在式(3)的基础上进行2像素的扩充，这样面部特征点不会出现在图像的边界上，同时神经网络在训练过程中也可以学习一些背景图像的信息，增强了网络结构的健壮性。图2a为归一化处理前的图像，图2b为归一化处理后的图像。

Figure 2 Facial area relocation图2 面部区域重定位

3.3 CNN与Canny相结合的C-Canny算法

在测试集中，由于无法依靠pts文件进行面部区域重定位，因此如何定位基于3.2节的面部边缘扩充2像素的矩形区域，是本文所设计的神经网络在预测阶段的重要环节。为解决重定位问题，本文提出了一种C-Canny面部边缘检测算法，该算法可以显著地提高神经网络处理非训练集图像(wild photo)的准确性。C-Canny算法流程如图3所示。

Figure 3 Flow chart of C-Canny algorithm图3 C-Canny算法流程

3.3.1 面部区域预处理

首先，利用Haar分类器[9]进行面部区域初定位。Haar分类器又称Viola-Jones分类器，是Viola和Jones分别在2001年提出的算法。该分类器由Haar特征提取、离散强分类器和强分类级联器组成。其核心思想是提取人脸图像的Haar特征并使用积分图对特征进行运算，最终定位面部区域。虽然该算法具有一定的时效性，但是得出的面部区域与本文采用的基于面部边缘扩充2像素的图像相比，有着较大的差异。因此，本文借助Canny算法进行矩形边缘缩进，取得与网络模型训练阶段相类似的图像规格。Canny算法流程如下所示：

获取测试集输入图像的灰度格式，并进行高斯模糊处理：

(5)

F(x,y)=G(x,y)*F(x,y)

(6)

其中,F(x,y)为输入图像，G(x,y)为高斯函数,σ为正态分布的标准差。高斯函数与原图像进行卷积运算，消除灰度图像中的高斯白噪声干扰。之后利用Sobel算子计算梯度，获取到面部边缘集合。图4展示了边缘集合在图像中的具体位置(已将边缘集合进行描白处理)。其中图4a为没有经过消噪处理的图像，图4b为经过高斯模糊处理的灰度图像。经对比可得，经过高斯消噪处理的灰度图像能够较好地定位面部边缘。

Figure 4 Comparison of Gaussian blur图4 高斯模糊处理对比图

3.3.2 图像非极大值抑制

面部图像经3.3.1节处理后，还需进行非极大值抑制的工作。该过程是为了消除边缘集合中的伪边缘点，进一步细化面部边缘区域，得到更为准确的边界集合。

由3.3.1节Sobel算子处理后的图像，可以获得基于图像像素点的梯度幅值与梯度方向2个集合：

(7)

(8)

其中,gx,gy为Sobel算子计算出的图像内像素点的水平方向与垂直方向的梯度值。式(7)为图像信息的梯度幅值，式(8)为图像的梯度方向。

经过Sobel算子与8连通处理后的图像会出现基数较大的伪边缘点集合，因此为了去除掉这些伪边缘点，还需进行双阈值下的非极大值抑制。

因为每一幅图像的灰度分布值是不固定的，所以需要结合对应图像像素点的灰度分布直方图来进行高、低双阈值选取。3.3.1节的处理过程将原始图像转换为了由边界信息组成的特征点集合，其值域满足统计决策理论，因此可以借助Otsu算法来获得全局最佳的双阈值，其计算公式如式(9)所示：

(9)

其中，σ代表类间方差，σG代表全局方差，k1与k2代表图像像素值。Otsu算法以直方图中的方差、均值、均方差为参数，可以快速地计算出基于直方图统计的全局最优的2个阈值。如式(9)所示，Otsu算法将k1与k2的关系设置为3∶1的比例，然后将像素点集合中的灰度最小值赋给k2，计算出当前ψ的结果值并记录。之后，依次将k2向上取值，直到k1的值大于最大的灰度值。这时，取最大ψ值下的k1与k2为全局最优的滞后双阈值。

最后，进行非极大值抑制处理:

GH(x,y)=GNH(x,y)-GNL(x,y)

(10)

其中，GNH代表灰度值小于k1的像素点集合，GNL为灰度值大于k2的像素点集合。该表达式得出的结果为强边界点集合，其意义为：除去了强边缘点集中的弱边缘点，只保留真正的边缘点集合。这些细化后的面部边界信息，可为面部区域再定位打下基础。

3.3.3 面部区域再定位

由3.3.2节得出的新的面部轮廓点集合如式(10)所示，可以采用本节的方法获取基于面部边界扩充2像素的矩形区域，进而取得与训练阶段同规格的面部图像，提升面部特征点定位的准确率。由式(10)得到的细化后的面部边缘点集合如式(11)所示：

U(x,y)={x,y|x,y∈GNH(x,y)}

(11)

将集合U(x,y)经过面部区域再定位处理，可得到最终的面部区域。面部区域再定位伪代码如算法1所示。

算法1 面部区域再定位

输入：U(x,y)。/*经过C-Canny算法处理后的边缘点集合*/

输出:(sw,sh,w,h)。/*面部区域左上角坐标，图像的宽度与高度*/

步骤1 取细化边缘集合中中间行的最右节点：

w=(max(U(x,y))-min(U(x,y))).shape[0];/*shape[0]意为取(x,y)中的x*/

h=(max(U(x,y))-min(U(x,y))).shape[1];/*shape[1]意为取(x,y)中的y*/

sw=min(U(x,y).shape[0];

sh=min(U(x,y).shape[1];

midRow=sh+h/2;

步骤2 验证midRow所在行边缘节点的可用性：

if min(U(sh,midRow)) > 0.25 and min(U(sh,midRow)) < 0.75:/*人脸区域大小适中，满足重定位条件，移动图像左上角坐标点*/

sw=min(sh,U(midRow)).shape[0];

sh=min(sh,U(midRow)).shape[1];

跳转到步骤3；

else:

C-Canny算法找不到边界信息，图像质量不理想，跳过并返回步骤1，继续处理下一帧图像。

步骤3 平移面部区域：

/*处理面部图像区域，使其居中显示，并扩充2像素边缘宽度*/

w=w-sw+1;

h=h-sh+1;

sw=sw-1;

sh=sh-1;

面部区域再定位算法的实际表现如图5所示，其中图5a为在训练集上基于pts文件获得的面部图像与定位结果，图5b为在测试集上使用C-Canny算法处理后的面部图像与定位结果。两者均为基于面部边界扩充2像素的图像，将这些图像输入到本文设计的网络结构中，都能够较好地预测出面部特征点。

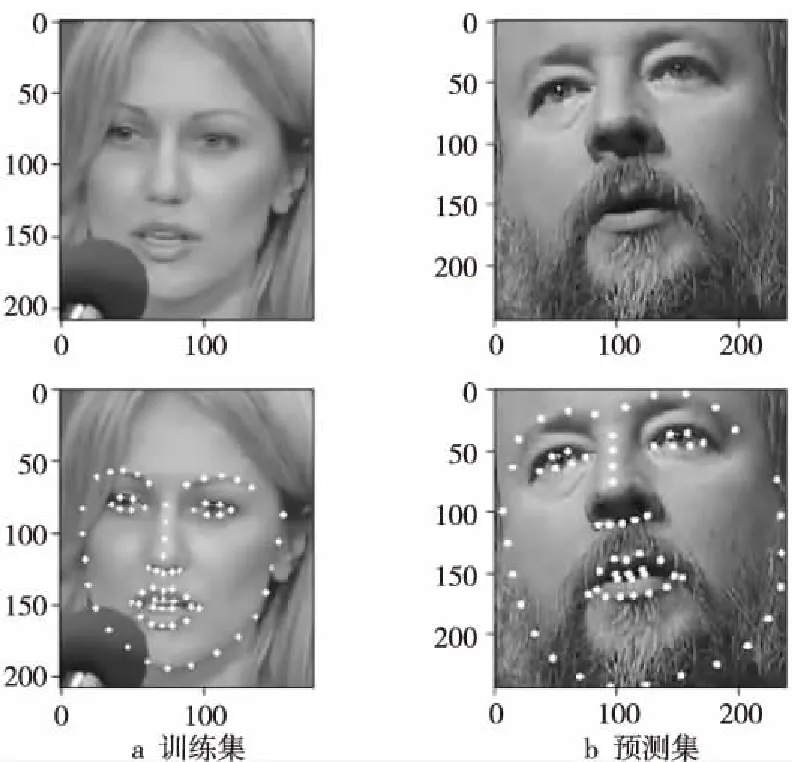
Figure 5 Relocation results on train dataset and predict dateset图5 训练集数据与预测集上的定位结果

4 实验与分析

4.1 实验数据

本文使用的实验数据是ibug网站提供的300-w[5]和300-vw[6]开源数据集。在300-w数据集中，每一帧图像都有着与之对应的pts文件,它记录着对应图像中的面部特征点坐标。而在300-vw的数据集中，面部图像是以avi格式的视频流文件进行存储的，本文通过FFmpeg工具将每一组视频流文件按帧分割成与pts文件一一对应的图像，总计得到了约22万个训练样本，排除掉不能识别面部区域的图像，最终得到了约20万个训练样本。

特征点信息如图6所示。

Figure 6 Landmarks of face图6 面部特征点分布图

4.2 评价指标

本文采用的损失函数是均方误差MSE(Mean Square Error),其定义如式(12)所示:

(12)

(13)

其中，yi是真实数据，Yi是预测的数据，wi为大于0的权重参数。在数理统计中,均方误差是指参数估计值与参数真值之差平方的期望值，是衡量“平均误差”的一种较方便的方法，可以评价数据的变化程度。MSE的值越小，说明神经网络结构具有越高的准确性。

4.3 训练方法

本文采用基于Tensorflow自定义的estimator框架进行网络训练，使用的编程语言是Python。因为训练样本数多达20万，为加速网络结构的训练速度，本文将实验样本数据转换为TFRecord文件类型。该文件类型采用的是tf.data数据格式，tf.data以并行输入的方式进行训练，达到加速I/O流的效果。训练样本按3∶1∶1的比例分为训练集、验证集和测试集，以提升网络模型的鲁棒性。实验环境为：NVIDIA 1066显卡与Intel i5 8300 CPU。训练总次数为20万次，其中单次训练的随机样本数为512个，并对输入样本采用0.2的舍弃因子，以避免过拟合的现象发生。

网络训练过程中的损失函数时序值如图7所示。在迭代训练5 000次以后，损失函数已经处于0.01～0.06。虽然在17 000次有1次较为剧烈的波动，但是其值依然很低(0.07)，仍是一个可以接受的范围。

4.4 结果与分析

图8为在数据集300-w和300-vw上，本文设计的网络结构与部分已有方法的实验结果对比。

与一些传统方法(ESR，LBF等)相比，本文所设计的网络结构取得了更低的损失函数值(降低了22.3%)，但与级联型神经网络(CasCNN)相比，在total dataset上的损失函数值略高(7.49%)。原因在于本文网络的训练过程中并未使用全集样本进行训练，而是采用随机样本训练的方法。该方法能够较好地避免模型在训练期间出现过拟合现象，代价则是在全局预测阶段使损失函数的值略高。本文设计的网络与级联型网络在common dataset上的损失函数相持平(4.85%)，出现这种现象的原因是:级联型的网络层基数较大，在训练过程中经过多层的卷积、池化运算，其损失函数在训练集上会呈现较低的结果值，但是该值不能作为评价神经网络优劣性的指标，因为其无法等同于在测试集上也能取得较低的均方误差值。从图8本文网络结构与CasCNN在challenge dataset中的数据对比也可得出：本文网络结构在处理非训练集时更具准确性与鲁棒性，并且因使用的是单层神经网络结构，在训练难度上明显优于级联型神经网络，方便网络模型后续更好地调参与优化工作。

图9a展示的是UVXYZ神经网络[11]的定位结果，图9b是SAN神经网络[12]的定位结果。

Figure 9 Prediction results of UVXYZ and SAN图9 UVXYZ神经网络和SAN神经网络的预测结果

图10为本文方法的预测结果。与基于3D卷集核的UVXYZ神经网络[11]相比，本文设计的网络结构因使用的是2D卷集核，能够避免图像向高维空间转换的时耗，提升了约15%的模型响应速度，并且能够准确定位数目更多的面部特征点。当处理面部有遮挡的图像时，使用SAN神经网络[12]会出现边缘轮廓点定位不准确的问题，而本文的网络结构借助Canny算法进行面部区域重定位，较好地避免了这种问题的发生，并在均方误差值上与SAN神经网络相比降低了约20%。

Figure 10 Prediction results of method in this paper图10 本文方法预测结果

综上所述，由本文设计的网络模型训练20万次即可达到一个较为稳定的结果，在面部特征点定位方面与现有的一些方法相比将均方误差降到了0.028，并将准确率提升了约15%。

5 结束语

进一步的工作将继续关注面部特征点定位研究，特别是对于3D卷积核的改进，不断优化本文的神经网络结构，使其能够准确定位如高曝光、低暗度、高遮挡等极端条件下的面部特征点。最终将特征点定位与面部识别结合在一起，实现基于视频流的活体检测系统。