价格随机条件下看涨期权折扣契约的应急供应链协调研究

黄冬宏，吴双胜，刘 浪

(华东交通大学 经济管理学院，江西 南昌330013)

随着经济的高速发展，供应链上的节点企业在获取高额利润的同时也面临诸多不确定因素带来的冲击，原有的平衡状态被打破。而供应链上的参与者作为理性的“经济人”在决策时必然以自身利润最大化为行为准则，进而导致双重边际化效应，使整个供应链利益受损。通过分析以往的文献[1-2]发现契约机制能很好地应对这一现象。数量折扣契约作为一种常用契约，是指上游供应商根据购买量给下游零售商相应折扣，旨在通过订货量实现对价格的控制。期权作为一种重要的金融工具能在规避风险的同时提高资产投资效率。鉴于此，有学者运用期权的方法展开对供应链风险管理的研究，如文献[3-4]。

目前，关于采用契约机制协调供应链的研究主要建立在单个因素基础上[5-9]。文献[5]以短生命周期产品为研究对象，考虑在随机需求的情况下零售商对短生命周期产品的定价和订购量的联合决策。文献[6]在随机需求的前提下构建了一种供应链随机模型来研究滞销品的销售问题，并采用目标与惩罚契约来协调供应链。文献[7]考虑具有贸易信用违约风险时运用数量折扣契约协调供应链的问题。文献[8]探讨了随机需求下供应商管理库存(vendor managed inventory，VMI)系统中供应商与多个零售商之间的相互作用，并通过仿真验证了该系统的有效性。文献[9]研究了在集中决策和分散决策下市场需求中断对零售商销售价格的影响，最后用数值分析对结果进行了检验。

在实际的市场经济活动中，当突发事件发生时，不仅市场需求会急剧变化，生产成本、供应链成员的风险态度等也可能会发生一定程度上的改变。因此，多因素扰动下如何通过构建契约实现供应链的协调更具现实意义[10-13]。文献[10]在需求不确定的前提下，研究零售商厌恶风险和制造商风险中性的二级供应链协调问题。文献[11]探究了零售商和供应商均风险厌恶且二者的厌恶程度不一样的供应链绩效问题，发现供销双方不同的风险厌恶程度对整个供应链系统的绩效有很大影响。文献[12]研究发现，当市场环境变化导致生产成本和市场需求同时发生改变时，调整期权契约能够使供应链再次协调。文献[13]在供应商的产量和零售商的需求量均为随机的情况下，研究了零售商和供应商在分散决策下的生产和采购问题。

以上研究都是在商品价格稳定的前提下展开的，没有考虑商品的价格受外来因素的冲击而发生变化的情况。文献[14-20]拓展了研究的前提条件，探究了在价格随机的前提下，通过相应的契约机制以及对基准情况下的模型进行改进使得原本失衡的供应链系统重新达到协调。而这些都是建立在单个契约的基础上展开的研究，并没有将不同种契约组合起来使用。

随着问题的复杂化程度不断加深，单一的契约模型已不能协调复杂情况下的供应链。将2种甚至多种契约糅合在一起使用成为研究的重点[21-24]。文献[21]采用合作博弈的方法，以批发价格机制为基准，建立了期权合约模型，研究了基于期权合约的制造商-零售商供应链协调问题，其研究结果表明期权合约可以协调供应链，实现帕累托最优。文献[22]研究了用期权的方式使回购契约模型达到供应链协调。文献[23]将期权合同机制引入救济物资供应链管理中，设计了一个具有2个交付步骤的期权合约，并建立了一个期权定价模型来估计供应链中2个成员的同一期权合约的不同价值。文献[24]将单向期权扩展为双向期权，并为双向期权的二级供应链系统开发了一个供应合同，分析了双向期权对零售商订单策略的反馈效应。

通过浏览期权与契约相结合的文献可知，将期权与数量折扣契约融合使用的研究极少。实际中，零售商可以通过购买一定数量的看涨期权的方式将市场风险过渡到供应商。而供应商作为博弈的主导者，可以借助数量折扣契约设计一系列订货量和批发价的组合清单来刺激零售商增加订货量，从而达到抑制自身风险过大的目的。2种契约的融合避免了一方风险过大的情况产生，实现了风险共担。对于协调供应链和巩固供销双方的合作关系都有一定的现实意义。

综上可见，虽然有一部分学者将价格随机波动引入到供应链管理领域，但是将价格随机与期权契约相结合的供应链协调研究较少，将价格随机、期权契约以及数量折扣契约相结合的研究则更少。因此，本文通过设置恰当的机制将价格随机以及这2种契约机制合理地糅合在一起，形成新的契约机制，以此来协调供应链，并对协调效果进行比较。

1相关参数及含义

本文模型中涉及到的参数及经济含义如表1所示。

表1相关参数及含义Table 1 Relevant parameters and implications

2价格稳定条件下的应急数量折扣契约模型

假设供应链成员均为风险中性和完全理性，销售商品为短寿命周期产品。零售商、供应商以及整个供应链系统的期望收益函数分别为

市场需求因突发事件而发生波动，同时市场价格保持稳定，此时，批发价为

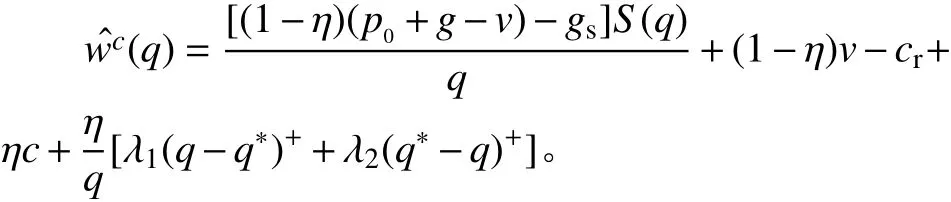
此时，数量折扣契约能协调供应链。(详见文献[18])。

3价格稳定条件下的应急看涨期权契约模型

以突发事件导致市场需求发生随机变化，而商品的市场价格保持不变为前提条件，将看涨期权契约引入到协调供应链管理领域。零售商作为理性的“经济人”，为确保自身在承担较低风险的同时获取高额利润，会按照期权订购和固定订购相融合的策略来确定订货量，按批发价w确定其固定订购量q，同时购买数量为m的期权，根据销售季节的市场需求状况决定是否执行看涨期权。此外，为保证模型的有效性，模型中的相关参数须满足

零售商、供应商和整个供应链的期望收益函数分别为

对式(4)分别求q、m一阶导数和二阶导数，得

由式(8)、式(10)和式(11)可得海塞矩阵

由式(8)可知

根据式(13)和式(14)，可知Hr为负定。故，分散决策模式下，零售商存在唯一的最优订货策略

由式(15)分析可得：供应商的价格策略(co,ce)对零售商的订货量有影响。由式(16)分析可得：随着批发价w(q)的增加，固定订购量将减少。当分散决策模式与集中决策模式下的最优订货量相等时，供应链重新达到协调。对集中决策模式下的供应链系统进行求解。

1)当q+m＞q*时，供应链期望收益函数为

对式(18)分别求q、m的一阶导数和二阶导数，得

由式(20)、式(22)和式(23)可得海塞矩阵。

根据式(25)和式(26)，可知Hh负定。因此，在集中决策下整个供应链系统能达到帕累托最优，即必然存在一组最优的订货决策令式(19)和式(21)为0，可得

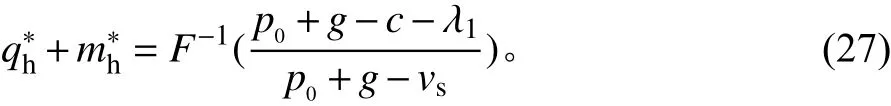
当集中决策和分散决策同时达到帕累托最优，即2种决策相一致时，供应链重新达到协调。联合式(15)和式(27)可得供应商的价格策略(co,ce)满足

0≤q+m≤q*

2)当 时，供应链期望收益为

对式(29)分别求q、m的一阶导数和二阶导数，得

根据式(31)、式(33)和式(34)可得海塞矩阵

根据式(31)可知

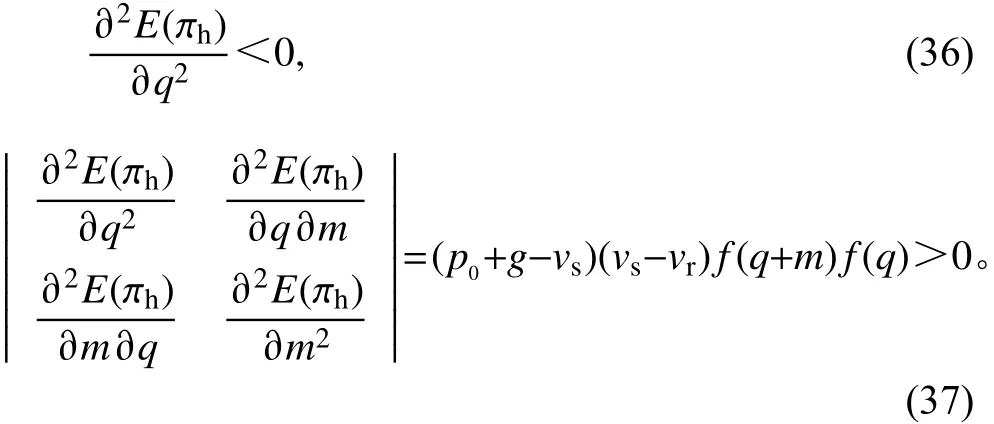
根据式(36)和式(37)，可知Hh负定。故在集中决策下零售商存在唯一的最优订货决策当时，供应链重新达到协调，供应商的价格策略(co,ce)满足

4 价格随机下的看涨期权折扣契约模型

当突发事件给正常运行的供应链系统带来巨大的冲击时，商品的供需关系发生巨大波动。商品价格由原先的p0变为p，并且满足dp=[p0+a(x-q)]dx，其中，a为市场规模数[14-20]。此时，单一的数量折扣契约已不能高效地协调供应链。因此，将数量折扣契约和看涨期权相融合，形成一种新的契约，来协调此种情况下的供应链系统。由此可得期权折扣契约模型。

零售商的期望收益函数为

供应商的期望收益函数为

整个供应链系统的期望收益函数为

对式(39)求关于q、m的一阶导数和二阶导数，得

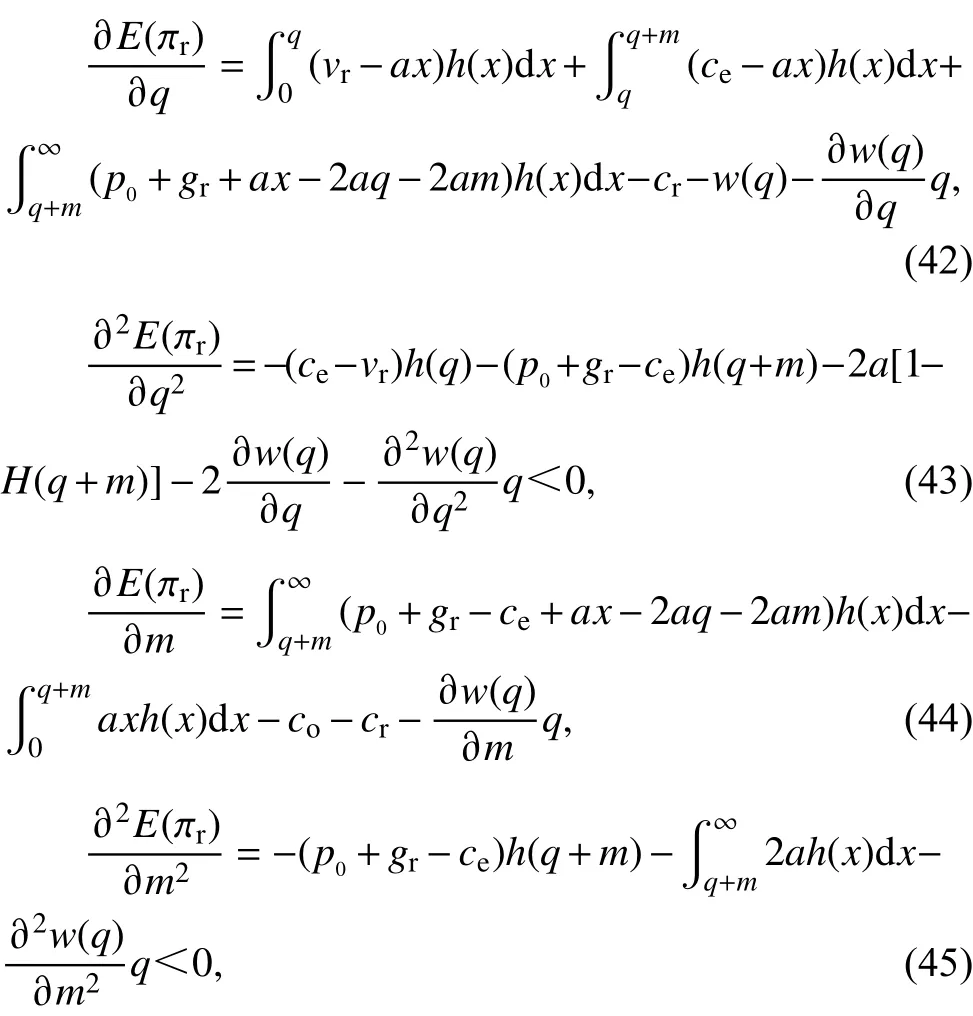
根据式(43)、式(45)、式(46)可得海赛矩阵

由式(43)可知

由式(48)和式(49)可知Hr负定。即零售商存在最优订货策略此时批发价w(q)在满足一定条件的基础上整个供应链系统才能达到协调。即，对于任意的

1)当q+m＞q*时，供应链期望收益为

对式(50)分别求q、m的一阶导数和二阶导数，得

由式(52)、式(54)和式(55)可得海塞矩阵

由式(52)可知

根据式(57)和式(58)，可知Hh负定。故整个供应链系统存在最优订货决策令式(42)、式(44)、式(51)和式(53)为0，并将其联立可得超越方程组，通过对相关参数赋值进行求解。

0≤q+m≤q*

2)当 时，供应链期望收益为

对式(59)分别求q、m的一阶导数和二阶导数，得

由式(61)、式(63)和式(64)可得海塞矩阵

由式(61)可知

根据式(66)和式(67)，可知Hh负定。故零售商存在最优订货量。令式(42)、式(44)、式(60)、和式(62)为0，并将其联立可得超越方程组，通过对相关参数赋值进行求解。

5算例分析

假设生产某产品的各项参数如下：p0=300元，cr=50元 ，cs=100元，gr=10元，gs=10元 ，λ1=10元，λ2=20元 ，a=0.005，vr=30元 ，vs=30元，另设co=10元 ，ce=175元。根据供销双方的易价能力，假定供应链的利润分配系数 η=0.5，不同情况下的市场需求分布不同，具体如下。

1)价格稳定状态下，市场需求服从X～N(10 000,3002)的正态分布；

2)价格随机变化且q+m＞q*时，市场需求服从X～N(20 000,3002)的正态分布；

3)价格随机变化且q+m≤q*，市场需求服从X～N(6 000,3002)的正态分布。

将上述参数及市场需求服从的分布代入超越方程组，用Mathematica软件进行算例仿真，结果如表2所示。

1)当市场遭遇突发事件，造成市场需求扩大、价格随机波动，采用数量折扣契约和看涨期权折扣契约均能实现供应链协调。采用数量折扣契约时，零售商收益、供应商收益、供应链收益由基准情况下的7 33 053、733 053、1 466 106上升为 1 435 760、1 435 760、2 871 520，均同比增加95.86%；采用看涨期权折扣契约时，零售商收益、供应商收益、供应链收益由基准情况下的7 33 053、733 053、 1 466 106上升为1 503 660、1 523 730、3 027 390，对应的收益同比增加105.12%、107.86%、106.49%。

2)突发事件造成市场需求缩小、价格随机波动，采用数量折扣契约协调供应链时，零售商收益、供应商收益、供应链收益由基准情况下的733 053、733 053、1 466 106下降为 392 396、392 396、784 792，均同比下降46.47%。采用看涨期权折扣契约协调供应链时，零售商收益、供应商收益、供应链收益由基准情况下的733 053、733 053、1 466 106下降为300 162、314 637、 614 799，对应的收益同比下降59.05%、57.08%、58.07%。

表2不同情况下供应链协调时的各参数及利润比较Table 2 Comparison of parameters and profits in supply chain coordination under different conditions

3)在价格随机波动的前提下，市场需求扩大时，采用看涨期权折扣契约相较于单一的数量折扣契约而言，固定订货量从1 9 827下 降为1 5 187，批发价却从177.5上升到187.8，同时买进数量为3 372的期权；市场需求缩小时，相对应的固定订货量由6 057下 降至2 614，批发价从178.2上升至202.9，买进数量为1 985的期权。

6结论

1)当突发事件造成市场价格随机波动以及商品的市场需求发生变化时，无论采用单一的数量折扣契约还是采用融合后的看涨期权折扣契约都能协调供应链，但是在协调的效果方面存在一定的差异。当商品的市场需求扩大时，2种契约机制均能有效地提高整个供应链系统及其节点上企业的利润，看涨期权折扣契约具有更好的协调效果，其利润比数量折扣契约单独协调时大约高出10%。此时，作为管理者可以通过看涨期权折扣契约在获取更大利润的同时降低自身的风险，实现双赢。在市场需求缩小时，2种契约机制虽然还能协调供应链，但是均不能扭转整个供应链系统以及供应链参与者利润大幅下降的局面。采用看涨期权折扣契约时的下降幅度更大，比数量折扣契约单独协调时高出约13%。因此，作为管理者可以通过提高产品质量、增加对市场的预测精度以及转换营销策略等方式来扭转这种局面。

2)看涨期权折扣契约增加了整个供应链系统抵抗外来因素冲击的韧性。供应链上的决策者可以通过对市场需求信息的预测决定是否执行期权的方式为自身争取最大的利益；零售商通过购买期权的方式将市场风险转移到供应商，而供应商则通过数量折扣契约来避免自身风险过大。2种契约融合使用，不仅提高了整个供应链系统以及供应链成员的利润，还实现了供应链成员之间的风险担当。

本文在供应链参与者均风险中性、信息对称的前提假设下，以看涨期权折扣契约为工具展开对突发事件下供应链协调的研究。在此基础上，可进一步拓展研究的前提假设，研究供应链参与者风险厌恶、供应商生产成本信息不对称以及零售商销售成本信息不对称情况下的供应链协调问题。