具有工序顺序柔性的车间调度问题研究综述

桂 林，张春江，李新宇

(华中科技大学 数字制造装备与技术国家重点实验室，湖北 武汉430074)

制造业是国民经济的重要支柱，而优化调度是整个制造系统的核心环节。调度的目的是在满足一系列约束的前提下，通过对资源的合理分配，使得某些指标达到最优[1]。学术界对于生产调度问题的研究，通常是在一系列假设的基础上，如工艺流程简单、加工路径固定、工艺约束确定等。但实际的生产加工过程往往具有复杂且可变的工艺路线和工艺约束，加工机器也往往具有不同的功能，因此具有柔性的调度往往更加符合实际的生产特点。化工、建筑、电子、纺织等行业的加工、装配和运输环节都可视为柔性调度问题[2]。因此，对柔性车间调度问题的研究具有理论意义和实际应用价值。

柔性车间调度问题的柔性主要分为3个方面[3]：工艺路线柔性、机器选择柔性和工序顺序柔性。工艺路线柔性是指工件在加工的过程中，有某一个或若干个加工工艺可以替换为其他不同的加工工艺；机器选择柔性是指在车间中有多台加工机器可以满足相同工艺的加工要求；工序顺序柔性是指工件的若干加工工艺在满足工艺约束的前提下仍可以具有不同的加工顺序。本文主要对现有研究中3种具有工序顺序柔性的车间调度问题(混合车间调度问题、分组车间调度问题和部分车间调度问题)的发展现状、存在的问题及未来的发展方向进行综述。

1定义和分类

在以往的研究中，研究人员通常将具有工序顺序柔性的车间调度问题描述为作业车间调度问题(job shop scheduling problem,JSP)和开放车间调度问题(open shop scheduling problem,OSP)2种问题的融合。实质上，这几种问题的不同是由于需要调度的工件具有不同的先后加工约束的工艺性质，因此有必要对不同性质的工件进行定义和分类。具体定义如下，工件类型如图1所示。

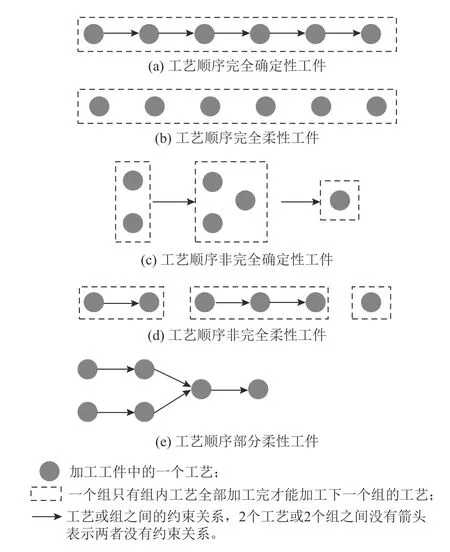
图1工件类型表示Figure 1 Workpiece type representation

1)工艺顺序完全确定性工件是指该工件任意2个加工工艺之间都有先后加工约束关系的工件，如图1(a)所示。这种工件用JCD表示。2)工艺顺序完全柔性工件是指该工件任意2个加工工艺之间都没有先后加工约束关系，加工工序顺序是任意的，如图1(b)所示。这种工件用JCF表示。3)工艺顺序非完全确定性工件是指该工件的所有工艺可以分为若干个组，在同一组内，所有工艺之间不具有先后加工的工艺约束，但不同组之间具有先后加工的工艺约束，如图1(c)所示。这种工件用JNCD表示。JNCD常见于加工、检测一体化车间中，如PCB生产车间。4)工序顺序非完全柔性工件是指该工件的所有工艺可以分为若干个组，在同一组内，所有工艺之间具有先后加工的工艺约束，但不同组之间不具有先后加工的工艺约束，如图1(d)所示。这种工件用JNCF表示。JNCF常见于模块化生产的生产车间中，如装配车间。5) 工序顺序部分柔性工件指的是在工件的所有工艺中，其中一个或若干个工艺与其他一些工艺存在先后加工的工艺约束关系，而与另一些工艺之间不存在先后加工的工艺约束的工件，如图1(e)所示。这种工件用JPF表示。具有工序顺序部分柔性的工件常见于物品回收再利用工业中，如对回收物品的拆卸过程。

当有一组待加工工件分别为JCD、JCF、JNCD和JPF时，则对这一组工件进行加工调度的问题分别为JSP、OSP、GSP (group shop scheduling problem，分组车间调度问题)和PSP (partial shop scheduling problem，部分车间调度问题)。当有一组待加工工件都是由JCD和JCF混合组成时，则对这一组工件进行加工调度的问题为MSP(mixed shop scheduling problem，混合车间调度问题)。在现有研究中，暂时没有关于工件由JNCF组成的车间调度问题的研究，本文暂时将这一类问题归于GSP中，称为GSP(II)。由上文对各种不同类型工件的描述不难发现，JCD和JCF分别是JNCD和JNCF的特殊情况，而JNCD和JNCF同时又是JPF的特殊情况。由此易知，JSP和OSP是MSP的特殊情况，MSP是GSP的特殊情况，GSP和GSP(II)是PSP的特殊情况，具体关系如图2所示。

2混合车间调度

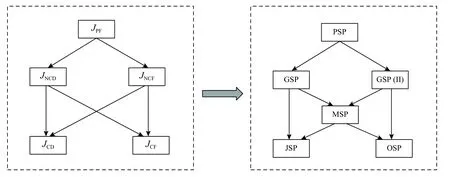
图2工件之间的关系和问题之间的关系Figure 2 Relationship between artifacts and problems

1985年，Masuda等[4]首次提出了MSP的概念。当假设车间中只有2台加工机器时，作者给出了一种精确算法。1987年，Ishii等[5]在上文工作的基础上添加了当机器工作速度可控时的假设条件，并给出了多项式时间内求解的算法。1999年，Shakhlevich等[6]考虑了具有m个加工机器和n个加工工件的MSP，证明了当m=3，n=3时，在工件的操作允许抢占的情况下，该问题为NP-hard 问题。2000 年，Shakhlevich等[7]对MSP的复杂度进行了总结。1998年Cheng等[8]对成批的MSP提出精确算法。2002年，Kis[9]探讨了2个工件分别为JCD和JCF，且工件的操作为非抢占时的MSP 的复杂度。2009 年，Liu等[10]对考虑准备时间和拆卸时间的双机MSP进行研究，并提出了一种近似算法。2010年，Cetinkaya等[11]探讨了批量的双机MSP，并提出了最优求解方法。2015年，Koulamas等[12]研究了当加工机器为3时的MSP，并提出近似算法。2015年，Dugarzhapov等[13]对可抢占的双机MSP提出一种新的多项式时间内求解的精确算法。2018和2020年，Liu等[14-15]对加工机器数为3时的MSP进行了研究，当同一工件在不同机器上的加工时间相同时，提出了4/3的近似算法。对于MSP，学者们大多从问题本身出发，对加工机器数较少或加工工件数为定值的问题进行研究，探索了MSP可用多项式进行求解的问题边界。

由于问题本身实际意义的限制，现有研究中很少有对大规模的MSP进行求解。1994年，Shakhlevich等[16]考虑了2个工件在m台机器上加工的车间调度问题，2个工件分别为JCD和JCF。研究结果表明，当目标函数为最小化最大完工时间或平均流经时间，且不允许工件操作之间的抢占时，该问题为NPhard问题，并提出元启发式求解方法。2000年Ferrell等[17]将一些常见的启发式规则应用于MSP，如先进先出、最短加工时间、非递减松弛和修正松弛法等。2012年，Liu等[18]针对MSP提出一种邻域结构，并使用3种元启发式法对问题进行求解。2016年，Nguyen等[19]使用元启发式法求解了MSP。2018年，Fan等[20]对不同的混合车间类型进行了分类。

对MSP的总结如表1所示。其中，m为加工机器数，n(j)为工序顺序完全确定性工件数，n(o)为工序顺序完全柔性工件数，m1、n1、n2分别为任意的加工机器数和工件数，k和L为一个确定的数值，r为所有工件中最大的加工工艺数。

3分组车间调度

GSP是在1997年的一个数学竞赛中被提出来的。当时的名称为FOPSS(first order parallel shop scheduling)[21]。

1998年之后，Blum等[22-24]对目标函数为最小化最大完工时间的GSP进行求解，定义了关键路径上的领域结构，并使用蚁群优化算法求解GSP。2002年，Sampels等[25]使用多种元启发式算法如蚁群算法、模拟退火算法、禁忌搜索算法等求解GSP。2005年，Liu等[26]对GSP定义了2种邻域结构，用禁忌搜索算法解决了GSP问题，最后又在算法中嵌入模拟退火算法以避免陷入局部最优。此后，Ahmadizar等[27-31]分别在2008年、2010年、2013年、2014年和2017年发表了与GSP相关的研究文章。其中，文献[27-29]研究了工件释放时间和工件加工时间不确定的随机GSP问题；文献[30]研究了带有序列相关准备时间和运输时间的GSP问题；文献[31]研究了带有随机工件释放时间、随机工件加工时间和模糊交货期的GSP问题。2018年，Kemmoe-Tchomte等[32]研究了目标函数为最小化最大完工时间的GSP，并用多次重启多级进化局部搜索算法求解。

在现有文献中，阶段车间调度问题(stage shop scheduling problem,SSP)与GSP具有相同的约束，因此这是同一问题的2个名称。1997年，Strusevich[33]研究了工件之间带有约束的SSP。2002年，Strusevich等[34]研究了加工机器数为3的SSP，并给出近似多项式算法。2003年，Kis[35]研究了工艺路线可变的SSP。2005年，Su等[36]研究了一种特殊的SSP，将工件的所有加工工艺分为2个部分，前一部分的加工工艺都具有先后加工的工艺约束，后一部分的加工工艺都不具有先后加工的工艺约束。2011年，Nasiri等[37]对目标函数为最小化最大完工时间的SSP建立了混合整数规划模型，并用禁忌搜索算法和遗传算法对问题进行求解。2013年，Dong等[38]对工件的前2个加工工艺没有先后加工约束，其他加工工艺具有先后加工约束的问题进行研究，并证明该问题为NP-hard问题。2015年，Nasiri等[39]使用蚁群算法对目标函数为完工时间的SSP进行求解。2019年，Mayer等[40]根据生产实例提出了带有并行机的SSP，并使用遗传算法对问题进行求解。

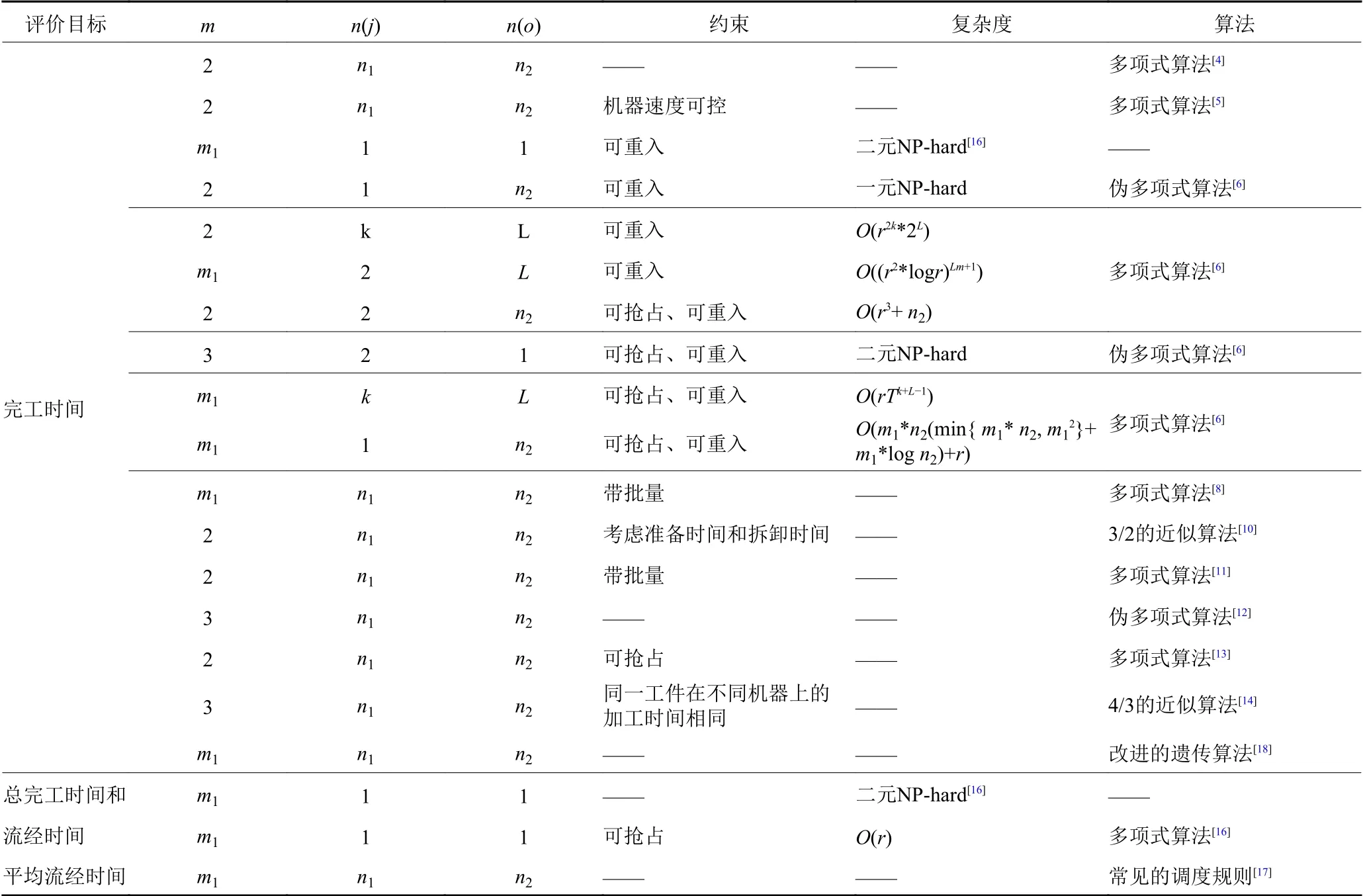
表1 MSP总结Table 1 Summary of MSP

对GSP的总结如表2所示。

4部分车间调度

在已有研究中，对于部分车间调度问题的研究可以归纳为2种类型。一种是从工艺规划角度对单一工件的工序顺序排序；另一种是从工艺规划与调度集成的角度对多个待加工工件的工序顺序排序。本文主要对后一种问题进行讨论和研究。

对于PSP的研究，大多数文献基于一个具体的生产实际展开。2002年，Gan等[41]对模具制造车间的工序顺序安排问题进行研究。2000年，Beach等[42]对具有柔性的车间调度进行综述，其中提及工序顺序柔性是柔性车间调度的一种重要形式。2005年，Ding等[43]提出了一种将遗传算法、神经网络和层次分析法相结合的混合算法，以求解具有多目标的PSP。2008年，Adenso-Díaz等[44]对具有双目标的拆卸车间的PSP进行研究。2011年，Nasiri等[45]对PSP建立了混合整数规划模型，并采用离散搜索和禁忌搜索相结合的方法求解该问题。2012年，Go等[46]提出了一种基于遗传算法解决汽车零部件拆卸序列优化模型；Zhu等[47]讨论了基于产品多样性所引起的复杂混合装配线最优序列的选择问题。2013年，黄学文等[48]总结了该问题中柔性工序顺序的类型和特点。2014年，Bentaha等[49]对工件拆卸时间为已知概率分布的随机变量的PSP进行研究；Quibell等[50]对加工机器数为3的PSP进行了研究，并提出了2种近似算法。2016年，黄学文等[51]提出一种工序顺序柔性描述方法和工件工序顺序的生成方法。2018年，Zubaran等[52]提出很多符合PSP的应用实例。

表2 GSP总结Table 2 Summary of GSP

最后为加深对PSP了解，这里例举文献[48]中某型号轴承的加工实例。该型号轴承的加工需要11道工序，其工序约束如图3所示，工序名称及约束情况如表3所示。箭头始端要先于箭头终端进行加工，如工序1要先于工序2加工，工序3要先于工序5和工序6加工，工序4要先于工序5和工序6加工。而工序3和工序4之间没有工序约束，可以先加工工序3，也可以先加工工序4。

5总结和展望

本文主要讨论了具有工序顺序柔性的车间调度问题。通过对工件类型的分类，本文更加清楚地描述了各种不同的车间类型。之后对研究具有工序顺序柔性的车间调度问题的现有文献进行分类和整理。由文献分析可知，对具有工序顺序柔性的车间调度问题的研究从20世纪80年代开始，研究大体上可以分为3种不同的问题：MSP、GSP和PSP。

图3某型号轴承加工工序约束图Figure 3 A certain type of bearing processing technology constraint diagram

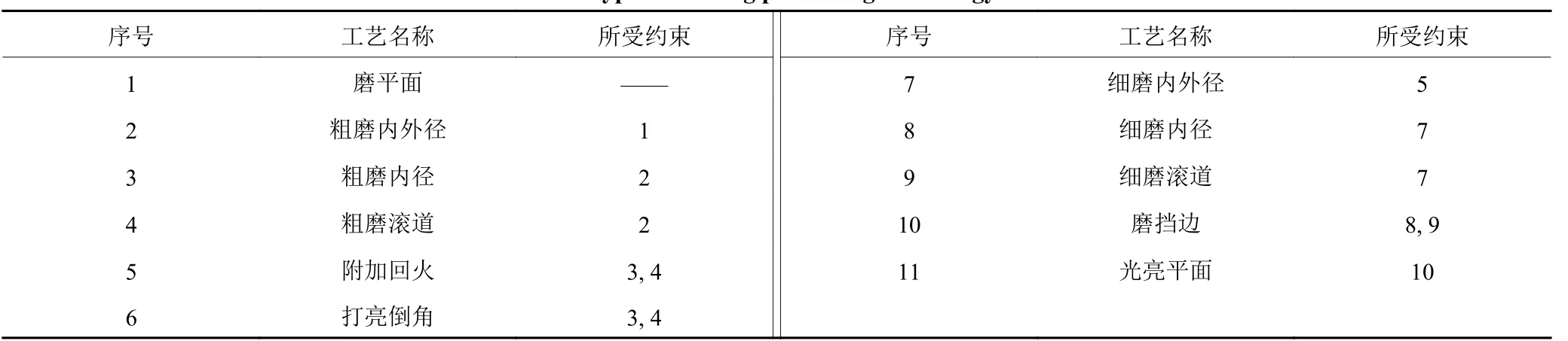
表3某型号轴承加工工序约束表Table 3 A certain type of bearing processing technology constraint table

对于MSP的研究大多关注问题本身。学者们对具有不同加工数量的机器、工件和不同约束条件的问题的复杂度进行了详细研究，并探索了可用多项式求出最优解的问题边界：当加工机器数为2，或当加工机器数和加工工件数为定值，且工件在加工时可抢占，可重入时，该问题可用多项式算法求解；在其他情况下，只能用近似算法对问题进行求解。

相比于MSP，很少有研究人员对于GSP本身进行研究，大多数研究集中于使用不同的启发式算法对具有不同约束条件、不同目标函数的问题进行求解。由于GSP与JSP在一定程度上的相似性，用于求解GSP的元启发式算法大都由解决JSP的元启发式算法改进而来。但GSP中含有“组”的特性，因此，在编码设计时大多用两阶段编码。

对于PSP的研究，本文主要从工艺规划与调度集成的角度对该问题进行分析。现有的研究大多基于一个实际的生产案例进行研究，提出了适用于该具体案例的解决方法。但很少有研究人员对实际问题进行抽象，因此PSP缺少对问题本身的研究和适用于通用问题的算法。

为了以后能够更好地开展具有工序顺序柔性的车间调度问题的研究，以下从4个层面提出现有研究中存在的不足和今后研究的发展方向。

1)问题层面。虽然现有的研究对于MSP和GSP都具有明确的定义，但从生产实际出发，现有的研究对问题挖掘不够充分。在现有研究中，MSP只包含JCD和JCF这2类工件。但在生产实际中，很少存在只具有这2 种类型的工件的加工车间。因此在MSP的研究中，需要在前2种类型工件的基础上，添加其他类型的工件，如JNCD、JNCF等，使问题更加贴合生产实际。对于GSP而言，需要根据问题独有的特性，挖掘出更多的有利于问题求解的知识，如基于问题特性的邻域等。此外，尽管GSP(II)类型的加工车间具有很大的实际应用价值，但到目前几乎没有对该问题的研究，因此在后面的研究中可以加大对该问题的投入。

2)模型层面。相对于其他类型的车间调度问题，具有工序顺序柔性的车间调度的研究较少。其主要原因是到现在为止，没有出现能够有利于问题求解的模型，使得将问题输入到计算机求解时不具有完备性或简洁性。虽然对各类问题，都有精确表达的混合整数规划模型，但该模型在问题求解上并不具有优势。因此需要建立具有问题特性并利于问题求解的模型。

3)约束层面。在以后的研究中，需要在其基础上添加其他的约束条件使得问题进一步贴近生产实际。比如考虑工件运输时间、准备时间、动态生产和多目标等。在添加一系列的约束后，不能仅改变问题求解的目标函数，而需要考虑添加的约束对于问题本身的影响，并在此基础上开发针对该问题和约束的有效搜索机制。

4)算法层面。大多数研究人员使用解决其他车间问题的策略和元启发式算法对具有工序顺序柔性的车间调度问题进行求解，使用的编码方式大多是两阶段编码等，这使得在问题求解时会出现结果质量不高，求解速度较慢等缺陷。因此在今后的研究中，需要在对问题进行深入分析的基础上，设计基于问题特性的编解码方式、邻域结构、求解策略等。