有能力限制的轴辐网络关键枢纽识别模型

李婷婷

(北京大学 城市规划与设计学院，广东 深圳518055)

轴辐网络(hub-and-spoke network)广泛应用于通讯和交通领域[1]。其中，枢纽选址问题[2](hub location problem，HLP)经常用于设计与分析轴辐网络。研究表明[3]，轴辐网络的枢纽很重要。然而，交通运输网络的枢纽因自然灾害、恶劣天气、设备故障、蓄意攻击等可能被阻断(interdiction，即禁止或停止运行)，从而产生严重不良影响。因此，有必要识别轴辐网络的关键枢纽以使阻断发生后损失最小化。

轴辐网络关键枢纽识别问题实质为枢纽阻断问题[4](hub interdiction problem，HIP)，目的在于识别轴辐网络中哪些枢纽被阻断后造成最大损失，即识别关键枢纽。与类似的网络阻断问题[5](network interdiction problem，NIP)、设施阻断问题[6-7](facility interdiction problem，FIP)相比，HIP的研究较少。Lei[8]提出了枢纽阻断中位问题(r-hub interdiction median problem，r-HIMP)，即从现有轴辐网络中识别r个关键枢纽，使得r个枢纽被阻断后轴辐网络中的最小总需求加权路径成本最大，并构建了双层规划模型。Parvaresh等[9]研究了考虑恶意破坏的枢纽网络设计问题，构建了双目标的双层规划模型(下层模型是HIP)，提出了基于模拟退火与禁忌搜索的启发式算法。Ghaffarinasab等[4]提出了3种类型的HIP，包括r-HIMP、枢纽阻断最大覆盖问题(r-hub interdiction maximal covering problem，r-HIMCP)、枢纽阻断中心问题(r-hub interdiction center problem，r-HICP)，分别构建双层规划模型并设计模拟退火算法求解。Ghaffarinasab等[10]对r-HIMP构建了双层规划模型，提出了隐枚举算法求解。Ramamoorthy等[11]对r-HIMP构建了双层规划模型，比较了基于对偶与最近分配约束的将双层规划模型转化为单层模型的方法，设计了Benders分解算法求解。

以上研究均采用双层规划模型解决HIP，然而均未考虑枢纽的能力限制。本文研究有能力限制的r-HIMP(capacitatedr-HIMP，Cr-HIMP)，考虑由于能力限制，枢纽被阻断后部分需求可能得不到满足的情况，构建双层规划模型，通过算例验证方法的有效性，以期为有能力限制的轴辐网络关键枢纽识别问题提供决策参考。

1模型

1.1 问题描述

Cr-HIMP考虑枢纽的能力限制，从现有轴辐网络的p个枢纽中识别r个关键枢纽。当r个关键枢纽被阻断后，使得网络的最小总需求加权路径成本最大，部分需求由于能力限制不能得到满足时则需要相应惩罚。Cr-HIMP涉及袭击者和防卫者两方，属于Stackleberg博弈，袭击者作为领导者，防卫者作为追随者，可以通过双层规划模型描述。其中，上层模型表示袭击者从现有轴辐网络的p个枢纽中挑选r个关键枢纽进行袭击，目标为最大化阻断发生后防卫者的最小总需求加权路径成本，下层表示防卫者在阻断发生后p-r个枢纽仍然正常运行的情况下选择最佳路线，目标为最小化阻断发生后的总需求加权路径成本。

本文假设枢纽被袭击后完全阻断而不能运行，同时遵循HLP的一般假设[12]。

1.2 模型构建

N为所有节点的集合，H为现有枢纽的集合。参数说明如下。p为现有枢纽的数量；r为被阻断的枢纽数量(即关键枢纽的数量)；wij为节点i、j之间的需求；dijkm为从节点i经过枢纽k和m到达节点j的成本，其中dijkm=αcik+βckm+γcmj，α、β、γ分别为集合线路、枢纽线路、疏运线路的折扣系数，cik、ckm、cmj分别为集合线路、枢纽线路、疏运线路的运输成本；θ为单位需求没有得到满足的惩罚成本；Ck为枢纽k的能力。变量说明如下。zk=1表示枢纽k没有被阻断，否则为0；xijkm表示阻断发生后从节点i经过枢纽k和m到达节点j的流量占i、j之间需求的比例；T为下层模型的目标函数值。

Cr-HIMP模型由上层模型(upper level problem,ULP)和下层模型(lower level problem,LLP)组成。

式(1)表示上层目标为最大化阻断发生后的最小总需求加权路径成本；式(2)表示r个枢纽被阻断；式(4)表示下层目标为最小化阻断发生后的总需求加权路径成本；式(5)表示节点i、j间的需求可能不全部满足；式(6)表示枢纽没有被阻断才能有流量通过；式(7)表示通过枢纽的流量不能超过其能力；式(3)、式(8)为变量约束。

1.3模型求解

式(4)等价于

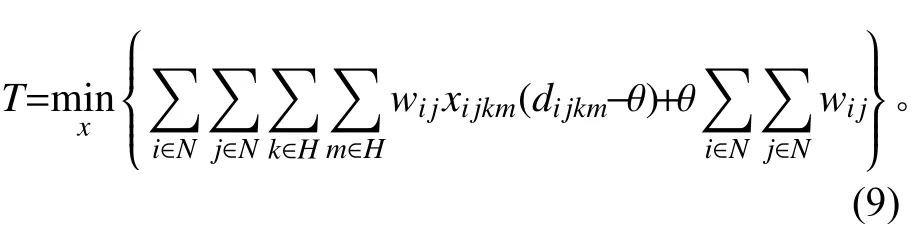
式(5)～(7)分别引入对偶变量λij、ρijk、ηk，LLP的对偶问题如下。

LLP-DF(dual formulation of lower level problem)：

令φij=-λij、δijk=-ρijk、πk=-ηk，则LLP-DF等价于LLP-NDF(new dual formulation of lower level problem)。

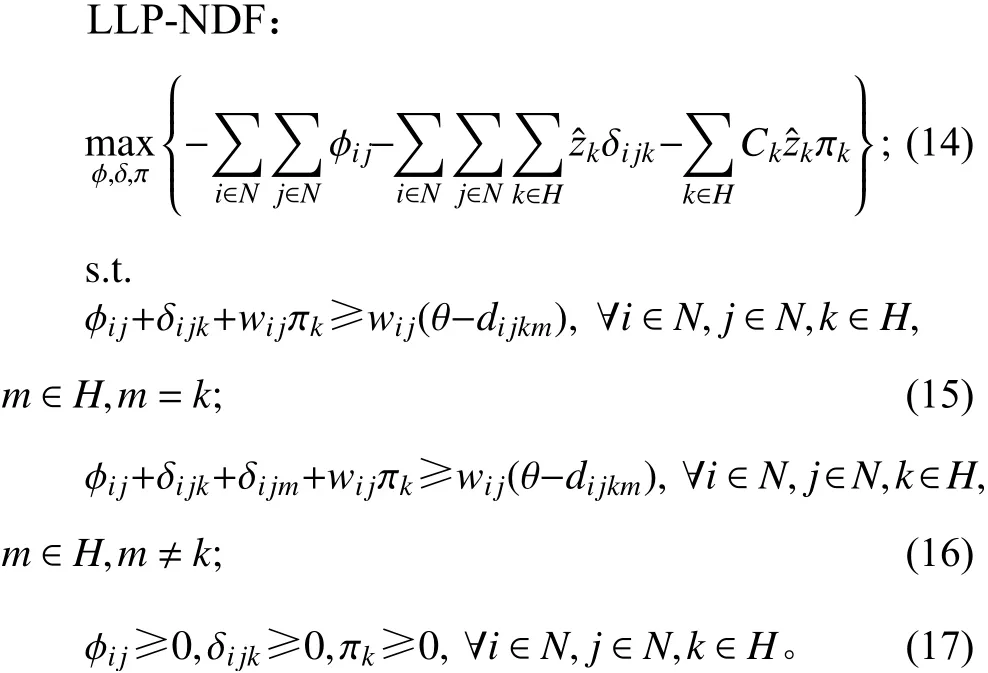
将LLP-NDF与ULP合并，得到max-max问题从而把双层规划模型转化为单层模型Cr-HIMP-S(singlelevel formulation of capacitatedr-HIMP)。

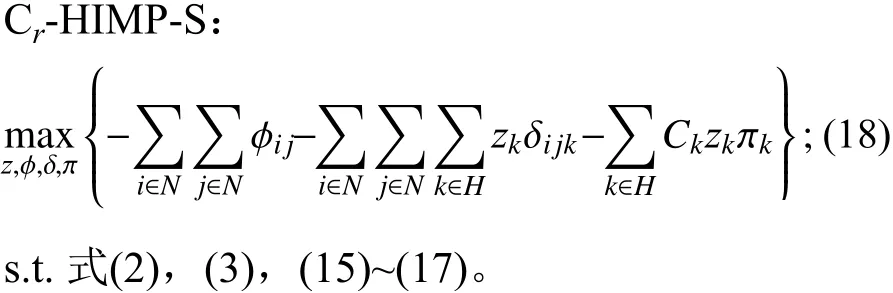
参考文献[13-14]将Cr-HIMP-S线性化，用变量

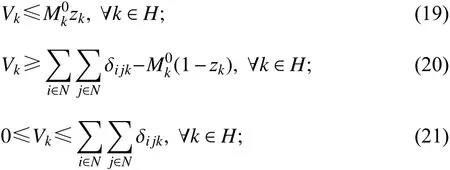
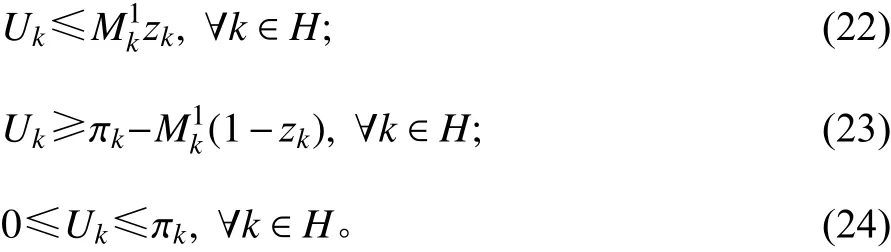
综上所述，Cr-HIMP转化为单层的线性模型Cr-HIMP-SL(single-level and linearized formulation of capacitatedr-HIMP)。

Cr-HIMP-SL：

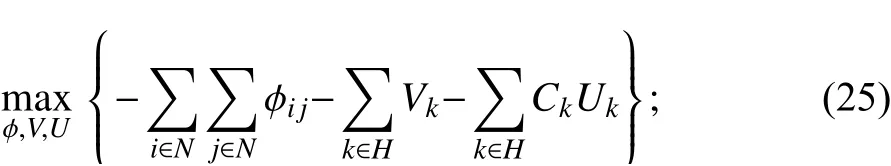
s.t.式(2)，(3)，(15)～(17)，(19)～(24)。

由于ρijk为约束(6)的影子价格，且 ρi jk≤0、δijk=-ρi jk，则δijk表示约束(6)右侧减少1单位后目标函数值变化的量。具体地，对于给定的i、j、k，当zk为1，i、j可以经过或者不经过枢纽k，若i、j间的需求都分配到最长路径i-k1-m1-j，对应的最大路径成本为此情况下目标函数值最大；当zk变为0时不能经过枢纽k，若i、j间的需求都分配到最短路径i-k2-m2-j(k2≠k，m2≠k)，对应的最小路径成本为此情况下目标函数值最小。因此，目标函数值的最大变化量为故

由于ηk为约束(7)的影子价格，且ηk≤0、πk=-ηk，则πk表示约束(7)右侧减少1单位后目标函数值变化的量。具体地，对于给定的k，当zk=1，由于增加1单位能力最多服务1单位需求：1)Ck减少1后，有1单位需求没有满足(被惩罚)，Ck减少1前，该1单位需求分配到k且经过最短路径i1-k-m3-j1(对应的最

短数

路值

径变

成化

本为

为

θ-

ddii11jj11kk mm33

；

=

mi2,

j,i

)mnC{

dk减i

jkm少})，1后

此，情有况1

下单

目位

标需

函求不能分配到k且经过最长路径i2-k4-m4-j2，对应的最大路径成本为di2j2k4m4=i,mj,l≠akx,m{di jlm}，Ck减少1前，该1单位需求分配到k且经过最短路径i1-k-m3-j1(对应的最短路径成本为di1j1km3=mi,j,imn{di jk m})，此情况下目标函数值变化为di2j2k4m4-di1j1km3。因此，目标函数值的最大变化为max{ θ-di1j1km3，di2j2k4m4-di1j1km3}，故πk≤max{θ-di1j1k m3,di2j2k4m4-di1j1km3}，可取Mk1=max{θ-di1j1k m3,di2j2k4m4-di1j1k m3}为πk的有效上界。

综上所述，Cr-HIMP等价于Cr-HIMP-SL，后者为线性规划模型，可以使用商业优化软件求解。

2算例

以CAB数据集(the civil aeronautics board(CAB)data set)[15]为例，该数据包含美国25个城市(如表1所示)之间的航空客流需求与成本。另外，p个枢纽及其能力采用文献[16]的方法生成。为作比较，以下参数取与文献[11]相同的值：p=7，α=γ=1，β ∈{0.9,0.5,0.1}，r∈{1,2,3,4,5}。θ参照文献[17]分别取2 000、3 000、 4 000进行计算。在主频为3.20 GHz的Intel Core i5-6500处理器、内存8 GB、操作系统Windows 10环境下，使用优化软件CPLEX 12.2[18]对模型求解，结果如表2所示。

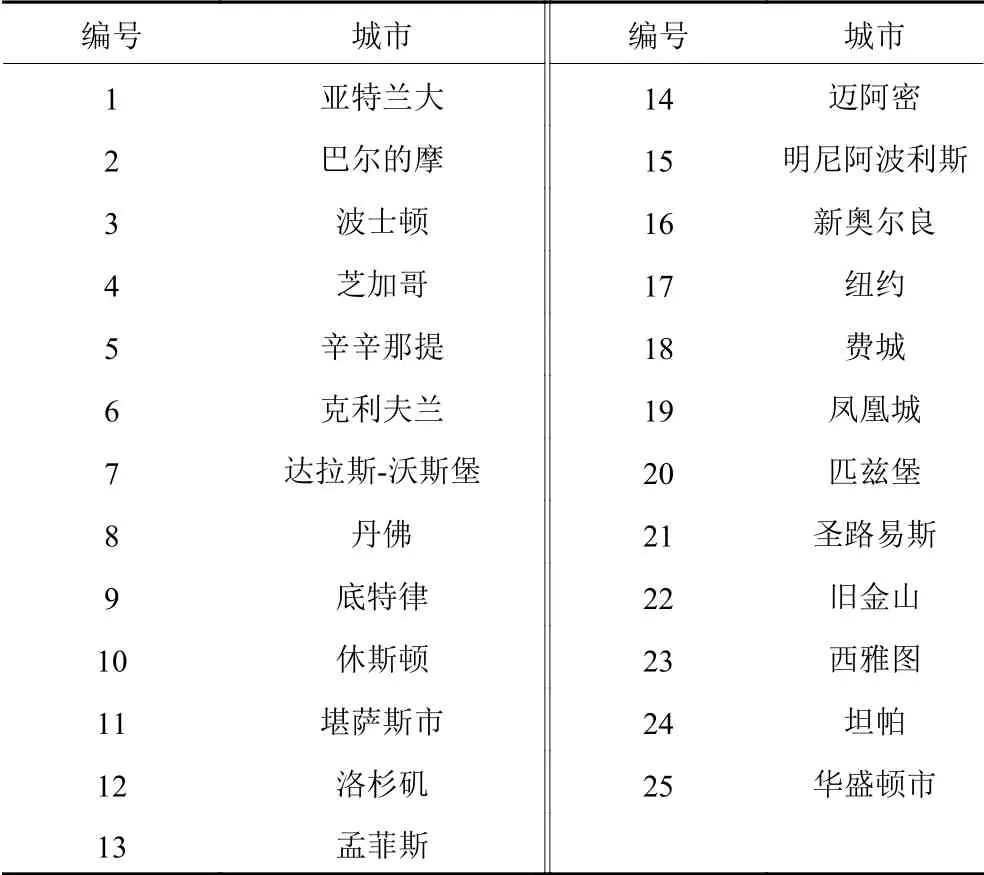
表1 CAB数据集中25个城市的编号[19]Table 1 The ID number of 25 cities in the CAB data set[19]

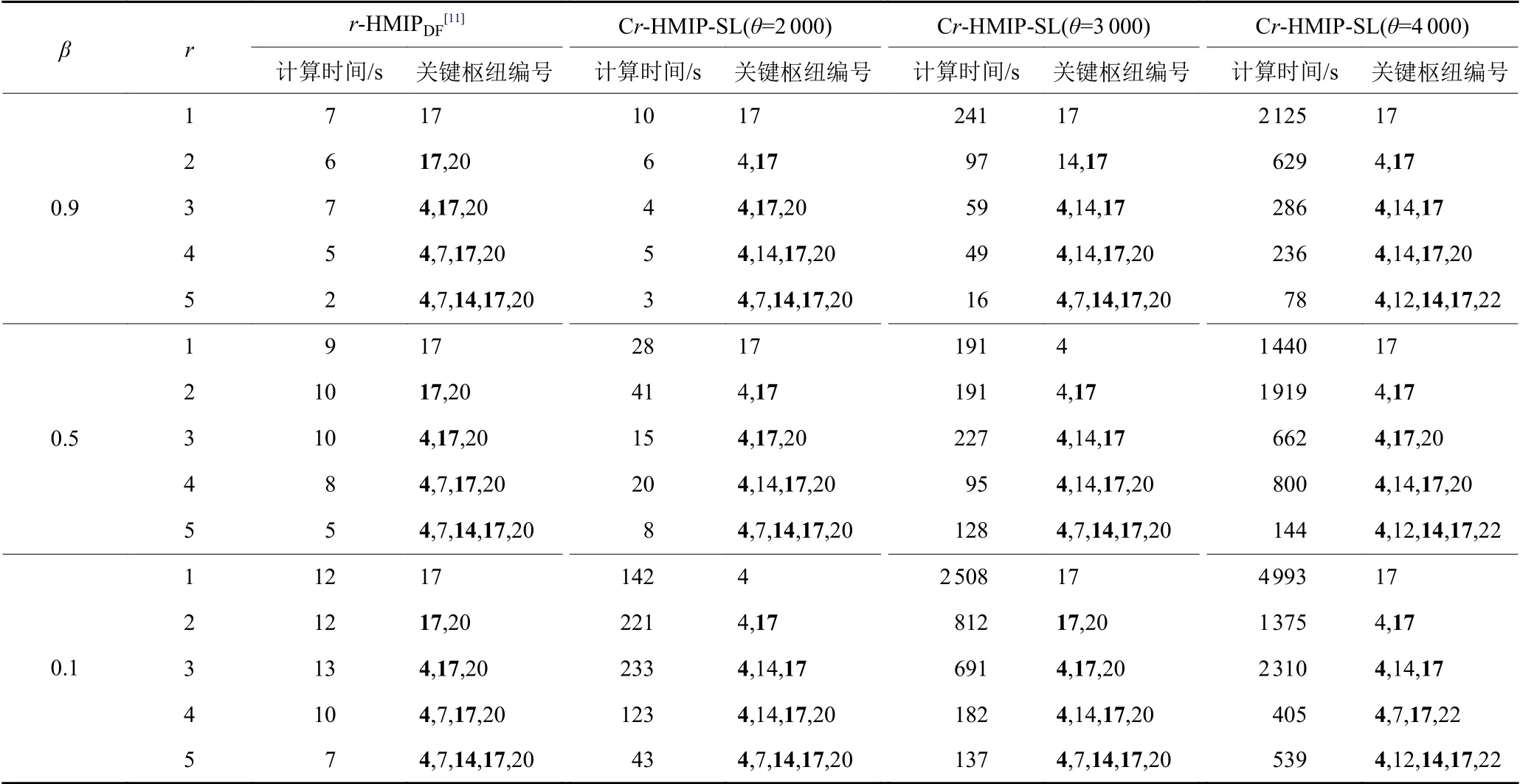
表2模型r-HMIPDF[11]与C r-HMIP-SL的求解结果比较Table 2 Comparison of the results of models r-HMIPDF[11]with C r-HMIP-SL

对于25个城市、7个枢纽的轴辐网络：文献[11]不考虑枢纽能力限制，模型r-HMIPDF[11]的约束数量为 4 390，变量数量为 5 015；本文考虑枢纽能力限制，模型Cr-HMIP-SL的约束数量为30 668，变量数量为 5 029。可见，考虑枢纽能力限制使约束数量和变量数增多。如表2所示，Cr-HMIP-SL计算时间普遍比r-HMIPDF[11]长，r-HMIPDF[11]计算时间均在15 s以下，Cr-HMIP-SL计算时间最长超过1h(当β=0.1、r=1、θ= 4 000时)。求解模型r-HMIPDF[11]与Cr-HMIP-SL得到的关键枢纽编号在某些情况下不相同，说明考虑能力限制与不考虑能力限制的关键枢纽识别结果会有差异。例如，当β=0.9、r=4，r-HMIPDF[11]对应关键枢纽编号为“4”“7”“17”“20”，而Cr-HMIP-SL对应“4”“14”“17”“20”。

对模型Cr-HMIP-SL，从表2看出，随着β减小或r减小或θ增大，计算时间普遍增加；当θ取不同值时，关键枢纽可能不相同，说明θ影响关键枢纽识别结果。例如，当β=0.9、r=3、θ= 2 000，关键枢纽编号为“4”“17”“20”，而β=0.9、r=3、θ=3 000或4 000，关键枢纽编号为“4”“14”“17”。然而，某些关键枢纽比较固定，在管理中可对这些枢纽加强设防。例如，当r=2，即使β、θ变化，“17”均为关键枢纽；当r=3或r=4，即使β、θ变化，“4”“17”均为关键枢纽；当r=5，即使β、θ变化，“4”“14”“17”均为关键枢纽。根据以上结果，判别出“14”“4”“17”关键程度依次增加，应实行越来越高级别的设防。

3结论

1)轴辐网络关键枢纽识别问题实质为HIP。在现有模型r-HIMP的基础上，增加枢纽能力约束，使用惩罚成本表示部分需求可能在枢纽阻断发生后不能满足，构建了双层规划模型，通过下层模型求对偶问题将双层规划模型转化为单层规划并线性化，以CAB数据集为例，通过CPLEX优化软件求解，验证了模型的有效性。

2)在不考虑枢纽能力限制模型基础上，增加枢纽能力约束使模型规模增大、求解时间变长，且考虑能力限制与不考虑能力限制模型的关键枢纽识别结果有差异。有能力限制的模型计算时间普遍随着β或r减小或θ增大而增加，且关键枢纽识别结果受θ影响。通过比较不同参数下的关键枢纽，可识别相对固定的关键枢纽并在管理中加强设防。例如，CAB数据集中，“14”“4”“17”为相对固定的关键枢纽，关键程度依次增加，应实行越来越高级别的设防。