基于游程检验的多元非参控制图

裴德昭，李艳婷

(上海交通大学 机械与动力工程学院，上海200240)

多元控制图是同时监控多个质量指标的控制图，很多学者对其进行了研究。Hotelling[1]提出了Hotelling T2控制图。Lowry等[2]提出多元指数移动平均(MEWMA)控制图。Croseier[3]提出多元累积和(MCUSUM)控制图。Makis[4]提出一种寻找最小平均成本及最优控制限的算法并设计了多元Bayesian控制图。Qiu[5]对多元控制图的研究进行了总结。

大部分多元控制图被设计用于具有正态分布数据的监控，在非正态条件下监控效果并不理想。根据Qiu[6]的分析，关于非正态分布监控的研究主要分为2个方向。1)对传统参数控制图的改进。一些学者(Borror等[7]，Stoumbos等[8]，Testik等[9])认为若参数变换合理，基于正态分布的控制图仍可用于非正态分布的监控。2) 发展面向未知分布的多元非参控制图。Qiu等[10]认为传统的参数转换只能改善控制效果，在很多运用中并不能达到理想的效果。同时，当受控样本过少时，参数估计准确程度的下降也会影响最终监控效率。因此，多元非参控制图在应对未知分布监控的情况时更有潜力。

Liu[11]基于数据深度设计控制图。Hawkins等[12]将未知参数向量转化为已知参数向量，设计自启动结构的EWMA控制图。Deng等[13]运用实时对比(RTC)的方法设计非参控制图。Li等[14]基于空间符号和数据深度设计了多元CUSUM控制图等。许多控制图应用需要一些前提条件。Sun等[15]运用支持向量机计算核距离，在T2控制图基础上设计了K控制图。Qiu[16]基于对数线性模型设计多元CUSUM控制图。Zou等[17]通过构造在椭球方向分布簇内仿射不变的符号检验，设计多元EWMA控制图。这些控制图需要足够的受控样本提取信息。Sullivan等[18]在Lowry等[2]的基础上提出自启动结构的多元EWMA控制图。Zou等[19]将套索算法(LASSO)变量挑选与贝叶斯信息准则(BIC)相结合设计多元统计控制方法。Zou等[20]基于空间秩设计多元EWMA控制图。当变量数过大时，这些控制图的表现效果并不理想。Chen等[21]提出的面向分布未知的EWMA控制图很好地解决了高维度监控的问题。

已有的多元非参控制图运用了很多非参数检验方法。Chen等[21]将Bickel[22]提出的多元经验分布的检验方式与Wilcoxon秩和检验结合，设计了EWMA控制图。Mukherjee等[23]提出了一种将Wilcoxon秩和检验与Ansari-Bradley检验相结合的Shewhart控制图。Zou等[17]提出基于多元符号检验的EWMA控制图。Li等[14]在空间符号检验的基础上，设计了CUSUM控制图。Boone等[24]提出基于Wilcoxon符号秩检验的Shewhart控制图。Zhou等[25]将多元拟合优度检验与最小生成树结合，设计SMMST控制图。Li等[26]基于Mann-Whitney双样本检验设计CPDP控制图。Chowdhury等[27]运用Cucconi检验设计Shewhart控制图。然而，很多检验对于小样本、高维度的数据并没有很好的检出力。Biswas等[28]在2014年提出了在高维数据且未知分布情况下的一种基于游程检验的双样本检验方法，并证明该方法在面对小样本、高维度数据时有很好的效果。

游程检验是以游程个数或游程长度为统计量所做的两分变量的随机性检验，用于检验一组变量数列有无趋势项，也可以检验两组变量有无显著差异，在总体分布不明确时也有良好的检验效果。在Nelson[29-30]之后，游程检验用于控制图设计的研究很少。Zhou等[25]运用最小生成树设计的自启动结构控制图，并论证了在较大漂移时比Zou等[20]的SREWMA控制图效果好。

针对受控样本少、高维度、分布未知、变量相关性未知等条件的数据监控，本文结合Biswas等[28]的基于游程检验的双样本检验，提出了非参控制图HAMEWMA。通过蒙特卡洛模拟，分析多种参数组合条件下平均运行链长(ARL)的表现。对比Chen等[21]列举的DFEWMA、SREWMA、SSEWMA和RTC控制图，证明在较大漂移时本控制图表现良好。选择Chen等[21]作对比的原因：首先其选取的变量数多，受控样本量少，变量之间有相关性，且选择了多种分布，满足横向比较的条件；其次这篇论文是本领域较新的研究成果，对近几年多个控制图进行比较总结，数据有很强的借鉴意义。

1多元非参控制图HAMEWMA设计

1.1基于Kruskal的最短汉密尔顿路径

设一个无向图G中有N个顶点，汉密尔顿路径H*是将N个顶点用N-1段连起来，且每个顶点的自由度不超过2。对于拥有N个顶点的图G，共有N/2条汉密尔顿路径。N-1段长度加和最小的路径，即为最短汉密尔顿路径。挑选最短汉密尔顿路径的方法有很多，例如，遗传算法[31]、粒子群算法[32]、随机蛙跳算法[33]等。但通常情况下，启发式算法得到渐优的结果，形成的最短汉密尔顿路径不唯一，导致检验统计量具有随机性。

Biswas等[28]运用Kruskal的思想得到最短汉密尔顿路径。先对图G中的所有边从小到大进行排列，以最小边为最短路径的入选段，依次入选；若之后的入选段与之前的段能形成环，或者加入后单个顶点的自由度大于2，则放弃该入选段；依次下去，直到遍历图G中所有边；最终得到唯一的最短汉密尔顿路径。

图1展示了将6个样本点排成最短汉密尔顿路径的过程。(a)表示图G中有A、B、C、D、E、F6个点，有21条边。(b)～(d)表示依次选择最短边(A,C)、(D,F)和(B,E)作 为入选段。(e)表示选择(C,F)作为入选段，与之前入选段不构成环且最大自由度在C、F取得，均为2，满足入选规则。(f)中(B,C)＜(A,B)，应考虑入选(B,C)，但其加入导致C的自由度大于2，不满足入选规则，故选择(A,B)。

根据上述形成的最短汉密尔顿路径设计游程检验统计量，并构造多元非参控制图。

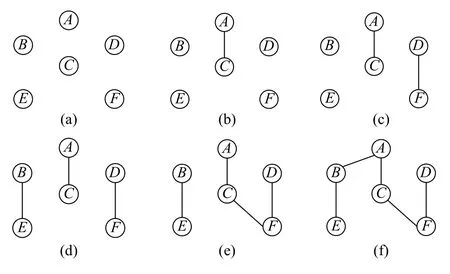
图1基于Kruskal的最短汉密尔顿路径形成示意图Figure 1 Schematic diagram of the shortest Hamiltonpath based on Kruskal

1.2多元非参控制图HAMEWMA的构造

原假设H0为所有的样本点来自同一分布，备择假设H1为S2中存在单个变点τ将S分为2部分，即前一部分样本点x1,···,xτ来自分布F0，后一部分样本点xτ+1,···,x m0+n来自分布F1，即

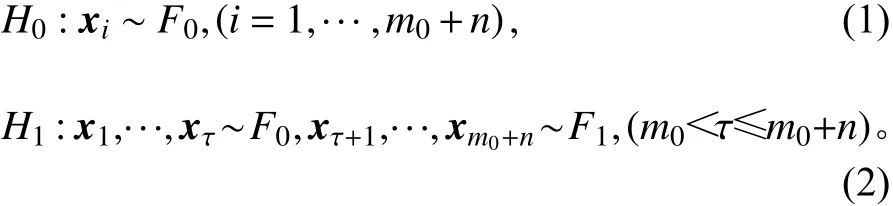
将S对应到图G中的m0+n个顶点，x i与x j之间的距离记为‖x i-x j‖，即样本点x i与x j间的欧氏距离。运用Kruskal方法得到最短汉密尔顿路径 H*， H*有m0+n-1段，每段记为Ut(1≤t≤m0+n-1)，得到检验统计量

其中,

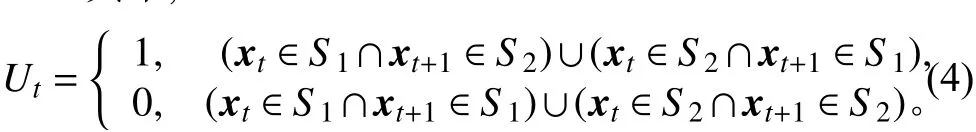
因为Tm0,n使用最短汉密尔顿路径 H*中的秩，以及x1,···,x m0+n间的可交换性，所以高维和单维均与分布无关。参考Mood[34]，在H0成立的条件下

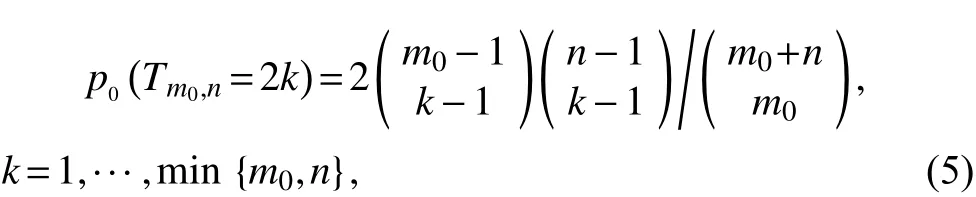
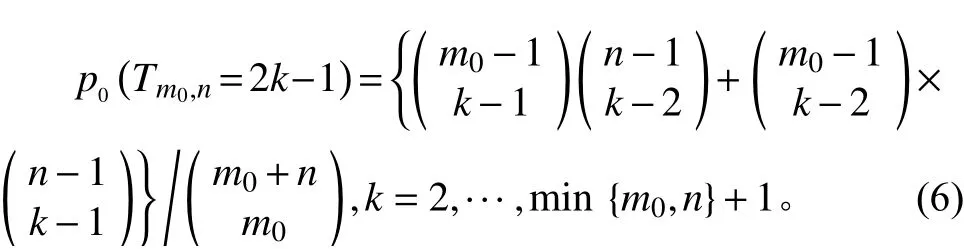
根据上述公式可得Tm0,n的概率分布。

若原假设H0成立，则 H*中会有2部分样本点混合均匀的趋势，导致T m0,n较大；若H0不成立，则H*中同一部分样本点会相距很近，导致T m0,n较小。令控制限为hm0,n，当T m0,n＜hm0,n时拒绝H0，表明存在变点且为检测样本中第n个样本点。

控制图常用的性能评价标准是平均运行链长ARL(average run length)，设每个检测样本中数据的出界概率为Pα，则ARL=1/Pα，需要调节控制限hm0,n达到预期的Pα。hm0,n由T m0,n的分布决定，而Tm0,n的分布是离散的且随着参数m0,n值的变化而变化，如表1所示。假设(m0,n)=(50,5)，Tm0,n最小为2，最大为11，共有10个可能值。根据式(5)和式(6)分别计算所取值的概率。当hm0,n=4，有0.013%的概率出界；当hm0,n=5，有0.160%的概率出界；当hm0,n=6，有0.561%的概率出界；当hm0,n=9，有33%的概率出界。

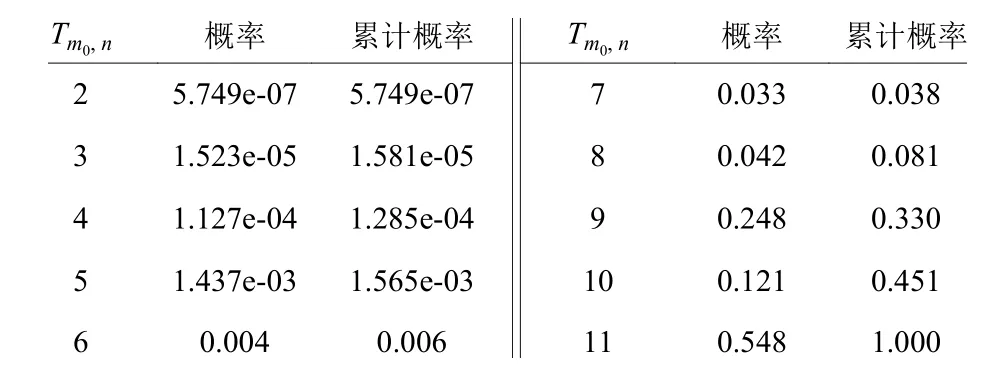
表1T m0,n的概率表Table 1 Probability table of T m0,n

本文考虑建立指数加权移动平均(EWMA)控制图，将历史数据里蕴含的过程信息累积，达到快速报警的目的。

根据式(7)得到EWMA统计量Zm0,n。E xm0,n(由式(5)和式(6)得到)为受控样本为m0，检测样本为n时的Tm0,n的期望。λ为平滑系数，EWMA控制图通常选择λ为0.05，0.1或0.2。因为λ取值较小时漂移更灵敏，同时参考Chen等[21]，本文取λ为0.05，0.1。

当m0固定时，n过大会增加求取hm0,n的计算量，同时，时间轴上相距较远监测点的影响研究价值不大。因此，考虑设置滑动窗口，当监控样本数大于滑动窗口宽度时，新的样本点会取代窗口中最久的样本点形成新的检测窗口。此外， H*是基于样本点间的欧氏距离生成的，需要保证每个变量的改变对总体距离的影响相同。因此，在监控前需依次对各变量归一化。p维样本向量根据式(8)、式(9)分别得到受控样本m0的均值、标准差，根据式(10)归一化。

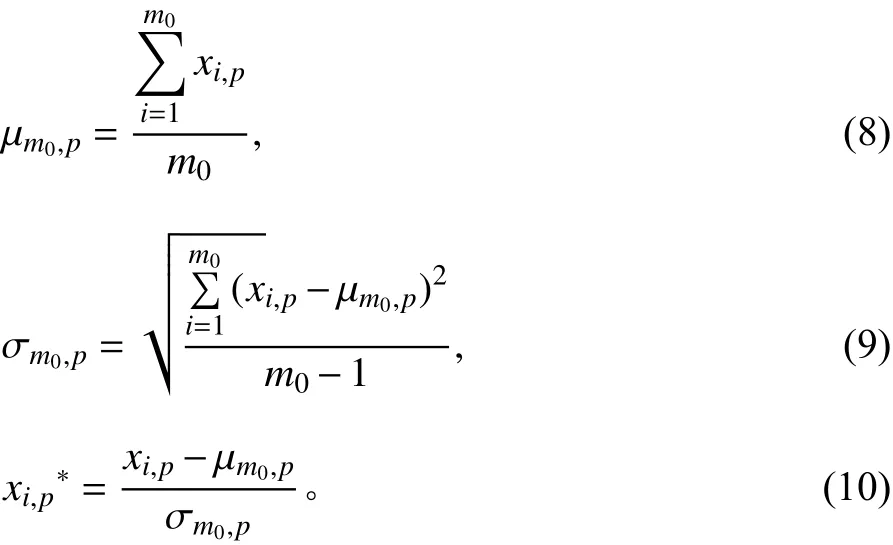
基于上述分析，本文提出HAMEWMA控制图。该控制图的平均运行链长计算方法如下。

步骤1S1={x1,···,xm0}为受控情况下的m0个p维样本向量，对所有变量数据归一化。

步骤2设定滑动窗口宽度wmax以及平滑系数λ的值。

步骤3设定L的值并计算控制线

步骤4设定HAMEWMA控制图统计量的初始值Zm0,0=0。

步骤5根据式(5)和式(6)计算样本组成( m0,n)为(m0,1),···,(m0,wmax)时 Tm0,n的期望，分别记为 E x1,···,

E xwmax。

步骤6根据式(12)得到Zm0,w。

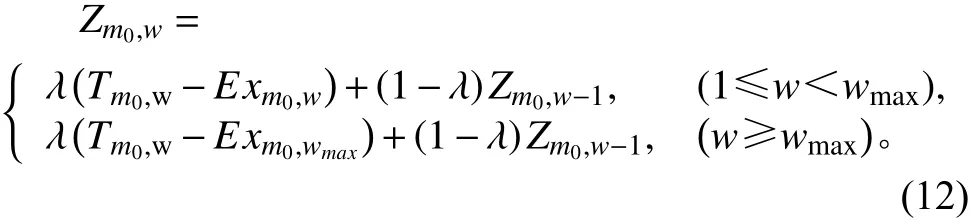
步骤7将步骤6得到的Zm0,w与LCL比较。若Zm0,w＞LCL，则继续计算 Zm0,w+1并比较其与LCL的大小；若Zm0,w≤LCL，记录此时的w-1为RL1。

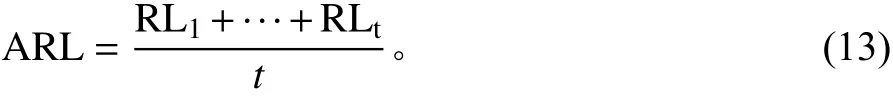
循环2 0 000次 得到RL1, ···,R L20000，根据式(13)计算当前的平均运行链长ARLnow。

2仿真检验

因为HAMEWMA控制图的优势为对高维度、小样本数据的监控，所以比较对象为此条件下表现优异的多元非参控制图：MEWMA控制图(Lowry等[2])，SSEWMA控制图(Hawkins等[12])，RTC控制图(Deng等[13])，MSEWMA控制图(Zou等[17])，SREWMA控制图(Zou等[20])和DFEWMA控制图(Chen等[21])。

2.1仿真设定

本文仿真是对于均值漂移的监控。漂移模型为

仿真过程中考虑6个因素的影响。

1)EWMA控制图的平滑系数λ，分别取0.05和0.1；

2)受控样本的数目m0，分别取15，25，50，75和100；

3)受控样本的维度p，分别取10，20，30，40和50；

4)漂移量的大小δ，分别取0.5，1.0，2.0和4.0；

5) 滑动窗口的宽度wmax，分别取5，10，15，20，25，30，35，40，45和50；

6)监控数据的分布类型，考虑3种分布。

①多元正态分布，记为Normp；

②多元t分布，自由度为ξ，记为 tp,ξ，ξ=5；

③多元Gamma分布。参照Stoumbos[8]的方法生成分布。令形状参数为φ，尺寸参数为1，记为G amp,φ，φ=3。

这3种分布均值向量为 X¯=(0,···,0)T，协方差矩阵均设定为其中，σii=1，σij=0.5|i-j|(i,j=1,2,···, p;i ≠j)。

2.2仿真结果

通过蒙特卡洛模拟得到在受控和失控状态下的平均运行链长，分别记作IC ARL(ARL in control)和OC ARL(ARL out of control)。在IC ARL相同的情况下，OC ARL越小，表明控制图性能越好。

2.2.1受控过程分析(IC ARL)

在设置初始平均运行链长为200的前提下，比较HAMEWMA控制图和一些具有代表性的多元非参控制图(DFEWMA、SREWMA、SSEWMA、MSEWMA、MEWMA、RTC)在监控受控数据时的平均运行链长表现(IC ARL)，结果如表2和表3所示。

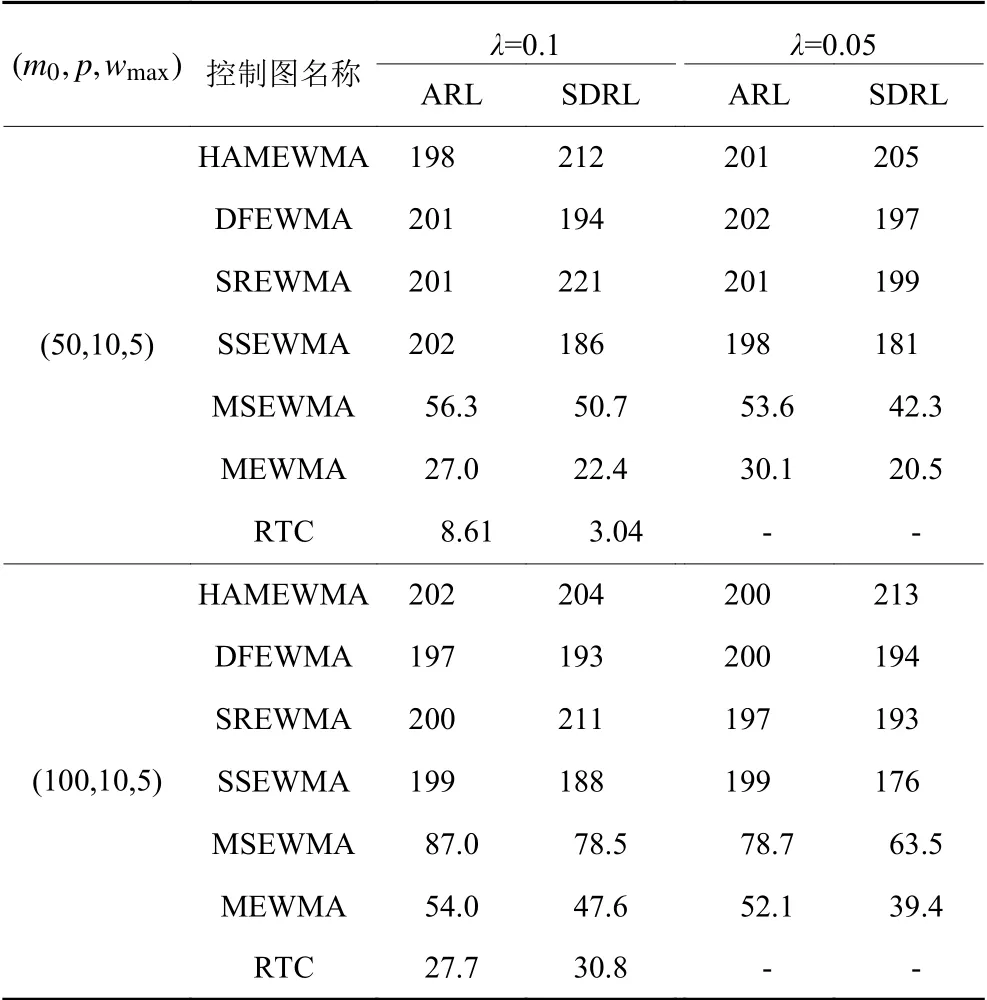
表2受控情况下对于多元正态分布HAMEWMA,DFEWMA,SREWMA, SSEWMA,MEWMA以及RTC的控制图表现Table 2 Control chart performance for the multivariate normal distribution of HAMEWMA,DFEWMA,SREWMA, SSEWMA,MEWMA and RTC under controlled conditions

可以看出，HAMEWMA控制图的IC ARL可以控制在200左右，且标准差也在200左右，有部分SDRL稍微偏离，但横向对比其他控制图，属于正常现象。表2中的SEWMA、MEWMA、RTC控制图的IC ARL明显低于初始设定值，在实际监控中会出现频繁报警的情况，说明HAMEWMA控制图在受控状态下的监控效果稳定。

2.2.2失控过程分析(OC ARL)

在不同分布类型、漂移量、滑动窗口宽度、数据维度、平滑系数及受控样本量的条件下，各控制图在受控状态下的整体表现情况如下。

1)滑动窗口宽度的影响。由图2可知，对于多元正态分布和多元t分布，当δ=0.5时，随着滑动窗口宽度的增加，ARL逐渐减小，窗口宽度为50的ARL是初始窗口宽度为5的ARL的70%，有大幅减小；当δ=1.0时，ARL基本不受窗口宽度的影响；当δ＞1.0时，随着窗口宽度增加，ARL逐渐增大并有趋于平稳的趋势。对于多元Gamma分布，当δ=0.5时，随着滑动窗口宽度的增加，ARL轻微减小后趋于平稳；当δ＞0.5时，随着滑动窗口宽度增加，ARL逐渐增大并趋于平稳。

2)数据维度的影响。由图3可知，对于多元正态分布和多元t分布，当δ＜4.0时，随着数据维度的增加，ARL逐渐减小；当δ=4.0时，ARL逐渐减小并趋于平稳。对于多元Gamma分布，当δ＜2.0时，随着数据维度的增加，ARL逐渐减小；当δ≥2.0时，ARL基本不受数据维度的影响，说明对于多元Gamma分布，HAMEWMA控制图对于低维度数据的较大漂移也有良好的监控效果。

3)受控样本量的影响。由图4可知，对于3种分布，随着受控样本量从15增至25，不同漂移量下失控ARL均明显减小；随着受控样本量从25增至100，失控ARL变化不明显。由此可得在一定的受控样本量范围内，HAMEWMA控制图的性能受样本量大小的影响并不大，可以实现对较小的受控样本的监控。

4)比较不同控制图性能及分析平滑系数的影响。表4选择m0=50,p=10进行控制图横向比较，其中，HAMEWMA控制图选择滑动窗口宽度为5。对表4的内容进行整理，得到图5(a)～(f)。该图展示了3种分布以及2种平滑系数时各控制图的ARL随漂移量变化的情况。分析3种数据分布，对于多元正态分布和多元t分布，当δ＞1.0时，HAMEWMA控制图表现最优；对于多元Gamma分布，当δ＞0.5时，HAMEWMA控制图表现最优。当δ较小时，DFEWMA，SREWMA，SSEWMA控制图在λ=0.05条件下表现更好；当δ较大时，DFEWMA，SREWMA，SSEWMA控制图在λ=0.1条件下表现更好。不同于上述现象，HAMEWMA控制图在λ=0.05时的表现优于λ=0.1时。

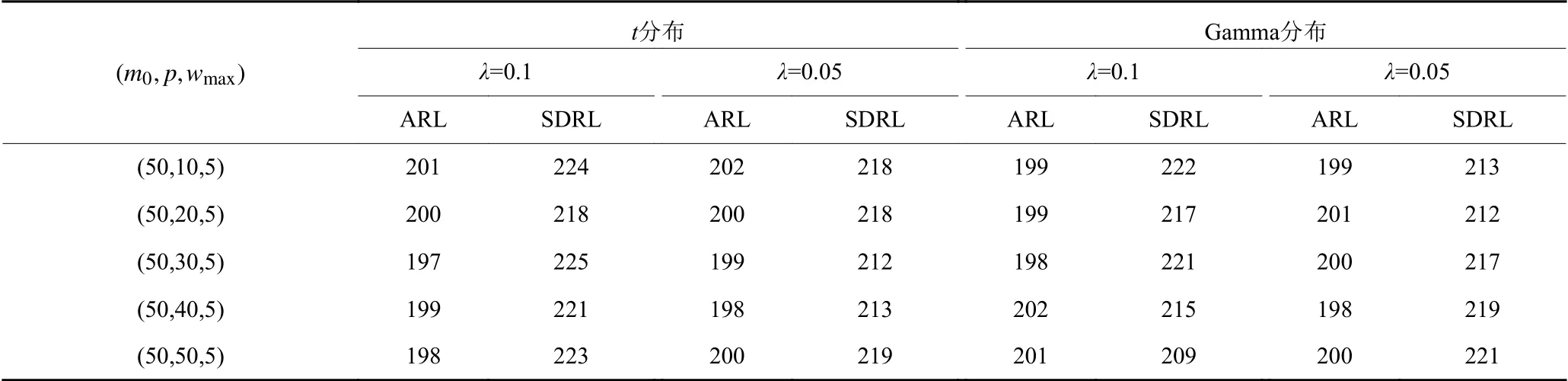
表3受控情况下对于多元t分布和多元Gamma分布HAMEWMA的控制图表现Table 3 Control chart performance for multivariate t distribution and multivariate Gamma distribution of HAMEWMA under controlled conditions

图2滑动窗口宽度与OC ARL的关系Figure 2 The relationship between sliding window width and OC ARL

图3数据维度与OC ARL的关系Figure 3 The relationship between data dimension and OC ARL

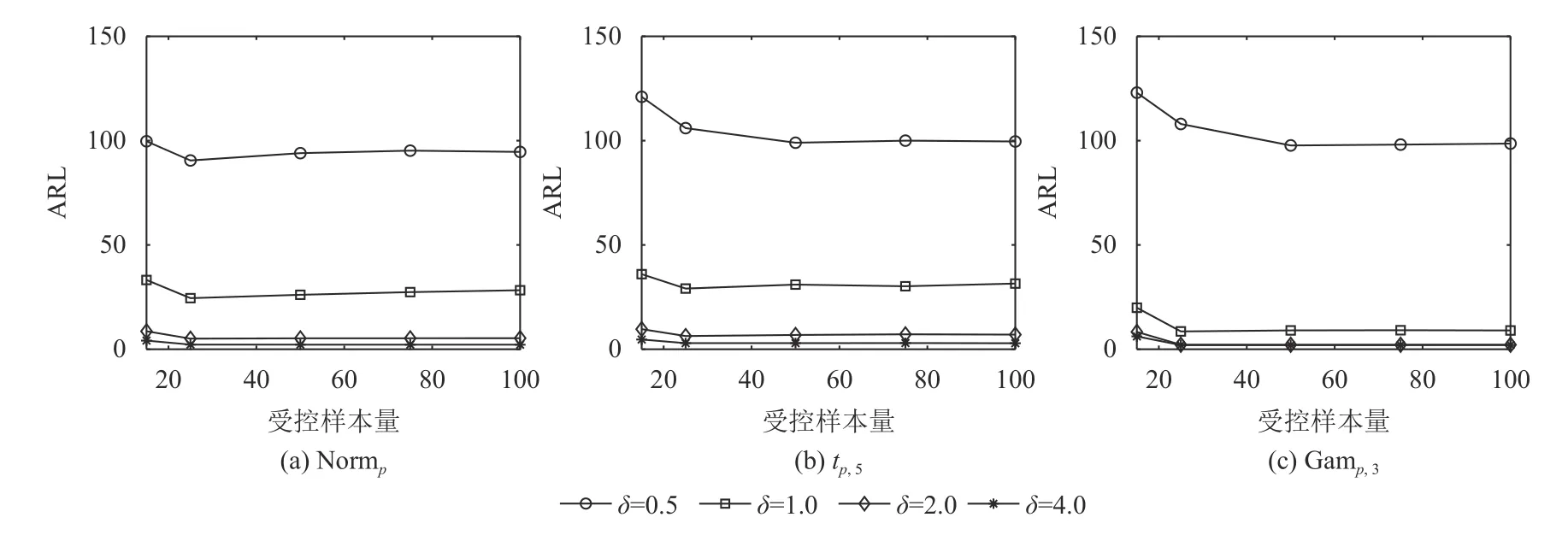
图4受控样本量与OC ARL的关系Figure 4 The relationship between controlled sample size and OC ARL

2.3仿真结果讨论

结合2.2的结果，分析仿真的6个因素对监控效果的影响。

1)平滑系数。不同于DFEWMA，SREWMA和SSEWMA控制图在λ=0.05时控制大漂移效果好，在λ=0.1时控制小漂移效果好，HAMEWMA控制图在λ=0.05时表现优于λ=0.1时的表现。因此具有较小平滑系数的HAMEWMA控制图监控效果好。

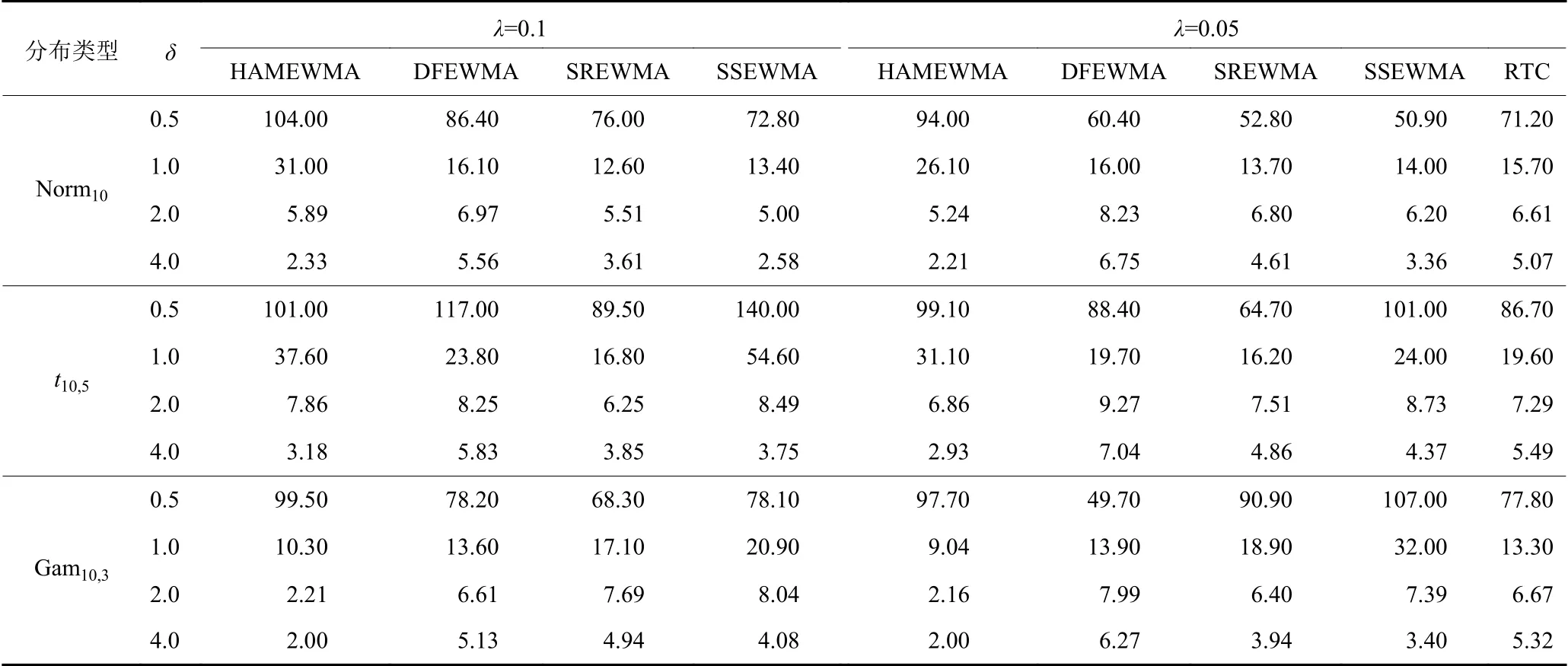
表4受控样本m0=50，数据维度p=10时HAMEWMA，DFEWMA，SREWMA，SSEWMA以及RTC的OC ARL比较Table 4 Comparison of OC ARL between HAMEWMA, DFEWMA, SREWMA,SSEWMAand RTC when m0=50 and p=10

图5 m 0=50,p=10时HAMEWMA，DFEWMA，SREWMA，SSEWMA和RTC控制图的OC ARL的比较Figure 5 Comparison of OC ARL between HAMEWMA, DFEWMA, SREWMA,SSEWMA and RTC when m0=50 and p=10

2)样本量。当受控样本量较小时，监控效果不佳，而随着样本量增大到一定范围，监控效果变优且基本不受样本量的影响。

3)窗口宽度。较大的窗口宽度会增强大漂移的监控效果，但会减弱小漂移的监控效果。结合具体分析，建议选择较小的滑动窗口宽度。

4)维度。数据维度越高，HAMEWMA控制图监控效果越好。

5)量。HAMEWMA控制图与其他多元非参控制图相比，对较小的漂移监控效果优势不突出，对较大的漂移监控效果良好，甚至达到参与比较的控制图中的最优水平。

6)分布。HAMEWMA控制图对3种分布均有良好的控制效果，对Gamma分布有更突出的表现。因此，HAMEWMA控制图对于未知分布的数据具有普适性，并推测对于非正态分布有更好的监控效果。

3实例检验

本文运用半导体制造过程中的高维数据来说明HAMEWMA控制图的有效性。采用的数据来源于Michael[35]的SECOM数据集，记录区间为2008年7月到2008年10月，由半导体制造过程中多个测量点的传感器采集得到。

数据集包含1 567个数据，每个数据由591个连续变量组成。数据集还提供了一个分类标签，表示经过生产线测试后是否合格(±1)。在这个数据集中，经过测试后合格的样本量为1 463个，记为合格样本；不合格的样本量为104个，记为不合格样本。数据分析的目标是根据传感器得到的数据进行建模并监控生产质量。

该问题属于高维数据监控，因此，考虑多变量统计过程控制(MSPC)的方法。预处理过程中移除117个不发生变化的变量和存在连续性缺失值的426个变量，剩余48个变量。在对数据进行监控分析前，判断数据的相关性及正态性。以受控样本为例，先将48个变量分别记作x1,···,x48，随机选取3个变量评估其相关性和正态性。本文选择x10、x20、x30进行分析。图6(a)～(c)分别为x10、x20、x30变量间的散点图，说明任意2个变量的联合分布不符合二元正态分布；图6(d)～(f)分别为x10、x20、x30的正态QQ图，表明边际分布也不全是正态分布。因此，多元正态性假设无效，本文期望设计的与分布无关的HAMEWMA控制图与传统控制图相比具有良好的鲁棒性。

运用HAMEWMA控制图对该数据集进行监控。从合格样本中随机抽取m0=50作为受控样本，设置控制图的基本参数为λ=0.05，ARL0=200，wmax=5。首先根据参数设置仿真得到控制限，其次按顺序依次监控从剩余合格样本中随机抽取的15个样本和不合格样本，得到如下控制图(图7)。在第25个数据时判定异常数据加入，控制图报警。这表明HAMEWMA控制图可以高效地监控高维数据流，有很强的实用性。

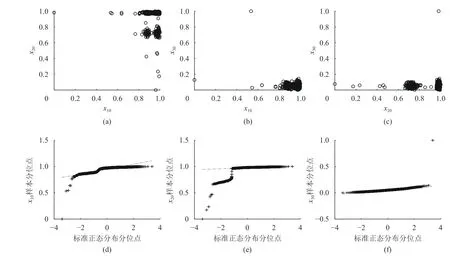
图6 x10,x20,x303变量的散点图及正态Q-Q图Figure 6 Scatterplots of x 10,x20,x30and normal Q-Q plots

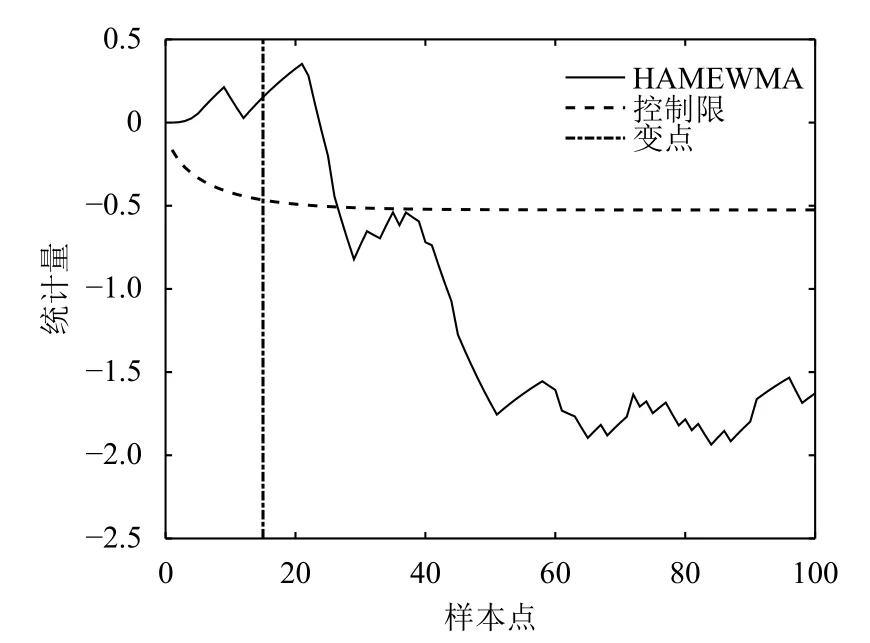
图7 HAMEWMA控制图对SECOM数据的监控效果Figure 7 Monitoring SECOM data by HAMEWMA control chart

4结论

针对受控样本少、高维度、分布未知、变量相关性未知等条件的数据监控，本文基于游程检验的双样本检验，设计了多元非参控制图HAMEWMA。通过仿真和实例分析，证明其在选择较小滑动窗口宽度，较小EWMA平滑系数的情况下，对具有较大漂移的高维数据有卓越的监控效果；对于非正态分布数据，HAMEWMA监控表现良好甚至优于对正态分布数据的监控，例如对Gamma分布数据的监控。此外，HAMEWMA控制图对小漂移的数据监控效果一般，需要后续的研究工作进行改进。与传统多元非参控制图相比，HAMEWMA控制图有良好的鲁棒性和监控优势，可在实际生产控制中运用。