基于一步法的金枪鱼生鱼片沙门氏菌生长数值模拟

李晓婷 李长城，2* 刘丽敏 张子叶 闫晓彤 方 婷，2

（1 福建农林大学食品科学学院 福州 350002 2 闽台特色海洋食品加工及营养健康教育部工程研究中心 福州 350002）

沙门氏菌是食品中最常见的食源性致病菌之一[1]，广泛存在于各类食品及加工环境中，食用被该菌污染的食品可导致食物中毒，具有较高的感染疾病风险。据美国疾病预防控制中心估计，在美国，全美每年大约120 万人感染沙门氏菌，其中23 000 人接受住院治疗，450 人死亡[2]。在中国，每年由沙门氏菌引起的食物中毒事件在细菌性食物中毒事件中也屡居首位，并且呈增长趋势[3]。目前，随着经济水平的提高和生活方式的改变，生鱼片或寿司等即食水产品越来越受到我国消费者的青睐。然而，生鱼片在食用前一般仅经过表面清洗、切割、整形等程序[4]，未经其它杀菌措施处理，食用生鱼片极易因交叉污染和温度滥放而导致沙门氏菌感染。近年来，美国曾多次爆发金枪鱼生鱼片或鱼糜产品感染沙门氏菌而导致大范围食物中毒的恶性事件[5-6]，进一步表明食用包括生鱼片在内的即食水产品具有较高的感染沙门氏菌的风险，应引起相关监管部门和消费者的重视。

预测微生物学模型是微生物安全风险监管的重要工具，它结合计算机可以预测食物中微生物的生长或残存变化[7]。传统的微生物生长预测建模采用两步法，包含两个步骤：第一步，收集不同温度条件下的生长数据，估计迟滞期和生长速率；第二步，建立二级模型，考察环境因子对迟滞期和生长速率的影响[8]。虽然传统的两步法是预测微生物学模型建立的标准方法，但其缺点是数据分析过程中累积误差较大。近年来文献报道，采用一步法对液态蛋中沙门氏菌[9-10]和土豆沙拉中金黄色葡萄球菌[11]的生长数据进行分析，通过全局优化残差平方和求解，同步构建初级模型和二级模型，其累积误差较小，曲线拟合优度好，并能较准确地估计微生物的生长参数。采用一步法开展预测微生物学建模具有显著的优势[12]。另外，生鱼片在加工、贮藏及销售过程中，温度可能随时波动[13]，而传统的生长预测建模大多仅考虑了恒定温度试验条件，缺乏对波动温度状态下的验证分析[14]。

本研究旨在通过一步法构建金枪鱼生鱼片中沙门氏菌静态及动态生长的数学模型，将所构建预测模型用于生鱼片中沙门氏菌的生长预测和风险评估。

1 材料与方法

1.1 材料与试剂

金枪鱼，福州山姆超市，真空包装后再于福建康普顿辐照技术有限公司辐照处理（剂量为8 kGy），并于-20 ℃冻藏。鼠伤寒沙门氏菌（CICC22956）、肠炎沙门氏菌（CICC21482），中国工业微生物菌种保藏管理中心（CICC）。

胰酪大豆胨琼脂培养基（TSA）、脑-心浸出液肉汤（BHI）、木糖赖氨酸脱氧胆盐琼脂（XLD），广东环凯微生物科技有限公司；利福平，北京索莱宝科技有限公司；蛋白胨粉，杭州微生物试剂有限公司。

1.2 仪器与设备

AIRTECH 生物安全柜，苏州安泰空气技术有限公司；Bag Mixer-400 均质拍打器，法国Interscience 公司；H-1850R 高速冷冻离心机，湖南相仪实验室仪器有限公司；SHP-250 细菌生化培养箱，上海精宏实验设备有限公司；KB115 低温恒温箱，德国BINDER 公司；Whirl-Pak-207 mL 无菌均质袋，美国Nasco 公司；VORTEX-5 漩涡混合器，上海习仁科学仪器有限公司；DX-200 高压灭菌器，德国Systec 公司。

1.3 细菌菌株及接种菌液制备

参照Fang 等[15]的方法逐步诱导鼠伤寒沙门氏菌（CICC22956）、肠炎沙门氏菌（CICC21482），使其产生耐利福平的抗性菌株，经平板（TSA/R）划线保存于8 ℃，每7 天转接至新鲜TSA/R 平板以保持其活性。每次试验前1 天，从保存沙门氏菌的TSA/R[8]平板上分别挑取一环单菌落接种至10 mL利福平质量浓度为100 mg/mL 的BHI 溶液中，并于37 ℃摇床（130 r/min）中培养18～20 h，然后在4℃条件下离心（5 000 r/min）15 min，菌体经无菌蛋白胨水清洗2 次后再悬浮于5 mL 质量分数为0.1%的蛋白胨水中。将上述两组沙门氏菌悬浮液混合，并梯度稀释至103～103.4lg（CFU/mL），备用。

1.4 恒定温度生长试验

无菌条件下，将金枪鱼鱼块切割成（5±0.2）g（尺寸约3 cm×2.5 cm×0.5 cm）大小生鱼片的，并置于无菌托盘上，再将上述制备的沙门氏菌悬浮液按点接方式接种至生鱼片样品中，接种量为50 μL。待已接种的生鱼片样品在生物安全柜中晾约15 min 后，将其装入无菌均质袋中，然后分别放置于8，10，12，16，20，25，30，35 ℃的恒温培养箱中培养，并按照预设的时间间隔取样。取样时，将15 mL 质量分数为0.1%的无菌蛋白胨水添加至样品袋，置于均质拍打器，正反两面各拍打2 min，均质液经梯度稀释后涂布于TSA/R 平板[8]，并于37 ℃条件下培养计数，最终生鱼片样品中沙门氏菌的浓度以lg（CFU/g）或ln（CFU/g）为单位计数。每个温度条件下的生长试验均独立重复2 次。

1.5 波动温度生长试验

前述恒定温度生长试验设置最高温度为35℃，而一般冷藏温度0～4 ℃，结合低温培养箱的实际可操作性，将培养箱温度设置于3～35 ℃范围内任意波动，以开展动态试验。本研究任意设置3 组温度-时间程序，最低温度和最高温度分别为3 ℃和35 ℃、4 ℃和30 ℃及10 ℃和30 ℃。试验时，按1.4 节的方法制备接种生鱼片样品，再将样品置于已预先设置温度-时间程序（图5a～5c 虚线所示）的变温培养箱中培养，并按照预设的时间间隔取样，取样方法如1.4 节所述。

1.6 数学建模和数据分析

1.6.1 初级模型和二级模型 沙门氏菌在金枪鱼生鱼片中的生长曲线呈滞后期、指数期和稳定期3 个阶段，因此，本研究选取Huang 模型[16-17]和Baranyi 模型[18]作为初级模型描述生鱼片样品中沙门氏菌的生长趋势。Huang 模型微分方程表达形式如式（1）：

式中，Y——t 时刻样品中沙门氏菌的浓度[ln（CFU/g）]；Y0，Ymax——初始菌浓度最大生长浓度[lg（CFU/g）]；μmax——最大比生长速率（h-1）；λ——迟滞期（h）；A，m——系数。

Baranyi 模型的微分方程表达形式如式（2）所示：

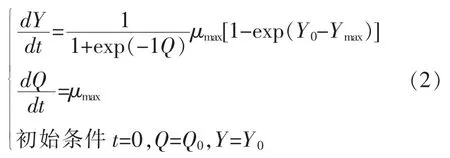
式中，Q——模型所引入的用以描述微生物生理状态的虚拟变量，其值随时间而变化，初值为Q0；Y0，Ymax和μmax的意义与Huang 模型中该参数意义相同。

金枪鱼生鱼片样品中，沙门氏菌的生长速率主要受温度的影响，本研究选取Huang Square-Root（HSR）模型[19]作为二级模型其表达式如式（3）：

式中，T——沙门氏菌所处的环境温度（℃）；Tmin——沙门氏菌的最低生长温度（℃）；μmax——沙门氏菌最大比生长速率（h-1）。

1.6.2 数值分析及非线性回归 从每个恒定温度条件下的两次独立重复试验中，各随机抽取一组数据组合成新的数据集{Y}，并用于一步法建模分析，同步构建初级模型（Huang 或Baranyi 模型）和二级模型（HSR 模型），简记为Huang-HSR 模型或Baranyi-HSR 模型。两种初级模型均包含有常微分方程，可通过经典的四阶龙格-库塔方法求解各恒定温度条件下沙门氏菌生长浓度的预测值{}[20]，再通过最小二乘法优化求解{Y}与的最小残差平方和RSS，如式（4）：

式中，N——总观察值的数量。

若将非线性回归分析需要估计的二级模型系数、最低生长温度及最大生长浓度等参数记为矩阵{P}，则Huang-HSR 模型的参数矩阵{P}={a，Tmin，Ymax，A，m}，Banranyi-HSR 模型的参数矩阵{P}={a，Tmin，Ymax，Q0}。本研究通过Matlab 软件编程实现四阶龙格-库塔方法联合最小二乘法求解矩阵参数{P}。

1.7 模型验证

通过一步法同步构建初级模型和二级模型，估计出矩阵参数{P}后，需进一步验证{P}的准确性。选取另一组独立的恒温生长试验数据及3 组波动温度生长试验数据对模型进行验证，并计算其均方根误差（RMSE），如式（5）所示：

式中，N——观测值总数；q——参数数量。

1.8 误差分析

通过Matlab 软件编程实现对误差（ε=Y^-Y）的拟合分析。

2 结果与分析

2.1 一步法数据分析及模型构建

本研究中，接种到生鱼片样品中的沙门氏菌的初始浓度为2.20～2.60 lg（CFU/g）。沙门氏菌属于嗜温菌[21]，处于低温环境时，其生长受到抑制，所以8 ℃贮存初期，生鱼片样品中沙门氏菌的数量未有显著增长，仅在贮存后期有所上升，然而，未能形成完整的生长曲线。当贮存温度为10～35℃时，生鱼片中沙门氏菌的生长状况良好，其生长曲线均包含迟滞期、对数期和稳定期3 个阶段（图1）。因此，数据分析时，仅选取10～35 ℃的生长数据用于建立模型。

一步法建模使用龙格-库塔法联合最小二乘法直接搜寻包含二级模型参数及最大生长浓度的矩阵{P}的过程，实际上是求解所有用于数据分析的生长曲线的全局最小RSS 值的过程。因此，当所有生长曲线全局最优化分析完成时，最小二乘法所预测的结果即为所求的参数矩阵{P}。使用一步法对10～35 ℃条件下生鱼片中沙门氏菌的生长数据（共97 个数据点）进行分析时，计算程序迅速收敛，统计结果及参数估计值分别如表1 和表2 所示。

由表1 可知，Huang-HSR 和Baranyi-HSR 模型的均方根误差（RMSE）分别为0.371 lg（CFU/g）和0.373 lg（CFU/g），且两者P 值均远小于0.05，说明两种初级模型（Huang 模型与Baranyi 模型）与二级模型（HSR 模型）的组合用于分析生鱼片中沙门氏菌的生长曲线时均表现良好。表2 列出了Huang-HSR 和Baranyi-HSR 模型的估计参数，两者估算的沙门氏菌的最低生长温度分别为6.91 ℃和6.83 ℃，均与文献[21]报道的沙门氏菌的最低生长温度接近。另外，由Huang-HSR 和Baranyi-HSR 模型的估计出的最大生长浓度几乎相等，分别为21.08 ln（CFU/g）[（9.15 lg（CFU/g）]和21.07 ln（CFU/g）[（9.15 lg（CFU/g）]，其标准差均为0.17 ln（CFU/g）[0.07 lg（CFU/g）]。虽然两种模型估计出的沙门氏菌的最低生长温度和最大生长浓度等参数相近，但是同作为初级模型的Huang 模型和Baranyi 模型对迟滞期的定义有着显著的差别。Huang 模型以显示的方式定义细菌的迟滞期（参数λ），并通过表达式描述迟滞期（λ）与最大比生长速率（μmax）之间的关系，如表2 所示，A=1.05，m=0.975；Baranyi 模型本身未直接定义细菌的迟滞期，其表达式中以隐式的方式引入了与迟滞期相关的参数Q0（-0.801）。因此，从Huang 模型对迟滞期这一参数对其定义更为清晰的角度出发[16]，本研究建议选择Huang 模型作为初级模型。根据估算出的二级模型参数，可知在本研究测试温度范围内，最大比生长速率随着温度的升高而增大（图2）。

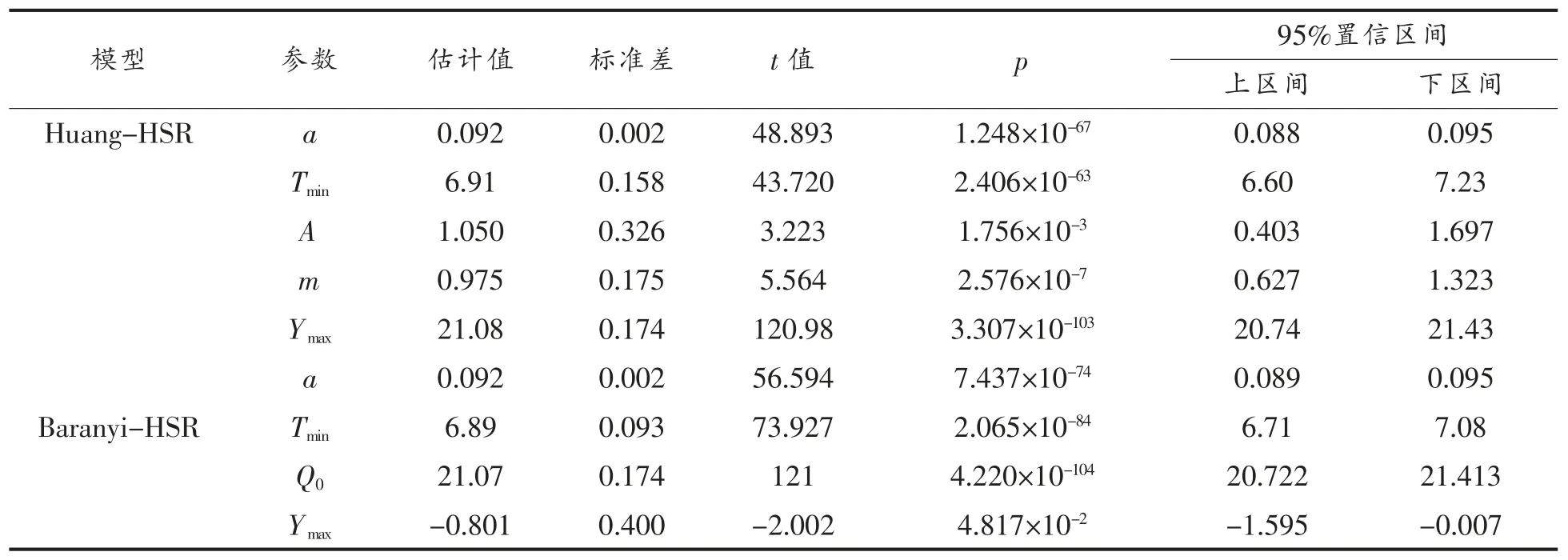
表2 Huang-HSR 和Baranyi-HSR 模型的参数估计Table 2 Estimated parameters of Huang-HSR model and Baranyi-HSR model

图2 一步法分析：温度对生长速率的影响Fig.2 Effect of temperature on growth rate obtained from one-step analysis

2.2 模型验证

2.2.1 恒定温度试验验证 本研究中，每个恒定温度（10～35 ℃）条件下，金枪鱼生鱼片中沙门氏菌的生长试验均独立重复2 次，其中一组独立试验数据用于前述的一步法建模分析，获取二级模型参数和全局最大生长浓度，即参数矩阵{P}，另一组独立试验数据用于验证所求解的参数矩阵{P}的准确性[12]。因为前述分析建议选用Huang 模型作为初级模型，所以验证过程仅选取Huang-HSR模型进行计算。图3 比较了10～35 ℃条件下验证试验的实测值与预测生长曲线之间的差异，共计79 个生长数据点纳入验证分析，总均方根误差（RMSE）为0.37 lg（CFU/g），表明恒温验证试验的生长数据均与模型估算的的生长曲线相接近。图4 表明恒温验证试验数据的残差（ε）服从均值为0.0 lg（CFU/g），标准差为0.36 lg（CFU/g）的正态分布。总体上，大约74.8%的实测数据的残差处于±0.5 lg（CFU/g）范围内，进一步表明模型的预测值与实测值较为接近。

2.2.2 波动温度试验验证 为了验证波动温度状态下模型的准确性，本研究另外设置3 组独立的温度在3～35 ℃范围内任意波动的验证试验，3 组独立试验的最低温度和最高温度分别为3 ℃和35 ℃、4 ℃和30 ℃及10 ℃和30 ℃（图5a～5c）。图5 分别比较了3 组波动温度条件下，验证试验的实测值与预测生长曲线之间的差异，共计71 个生长数据点纳入验证分析，整体均方根误差（RMSE）为0.44 lg（CFU/g），表明恒温验证的生长数据均与模型估算的的生长曲线相接近。图6 表明波动温度验证试验数据的残差（ε）服从拉普拉斯分布。总体上，大约79.0%的实测数据的残差处于±0.5 lg（CFU/g）范围内，表明一步法所构建的预测模型在波动温度条件下同样具有较为准确的预测能力。

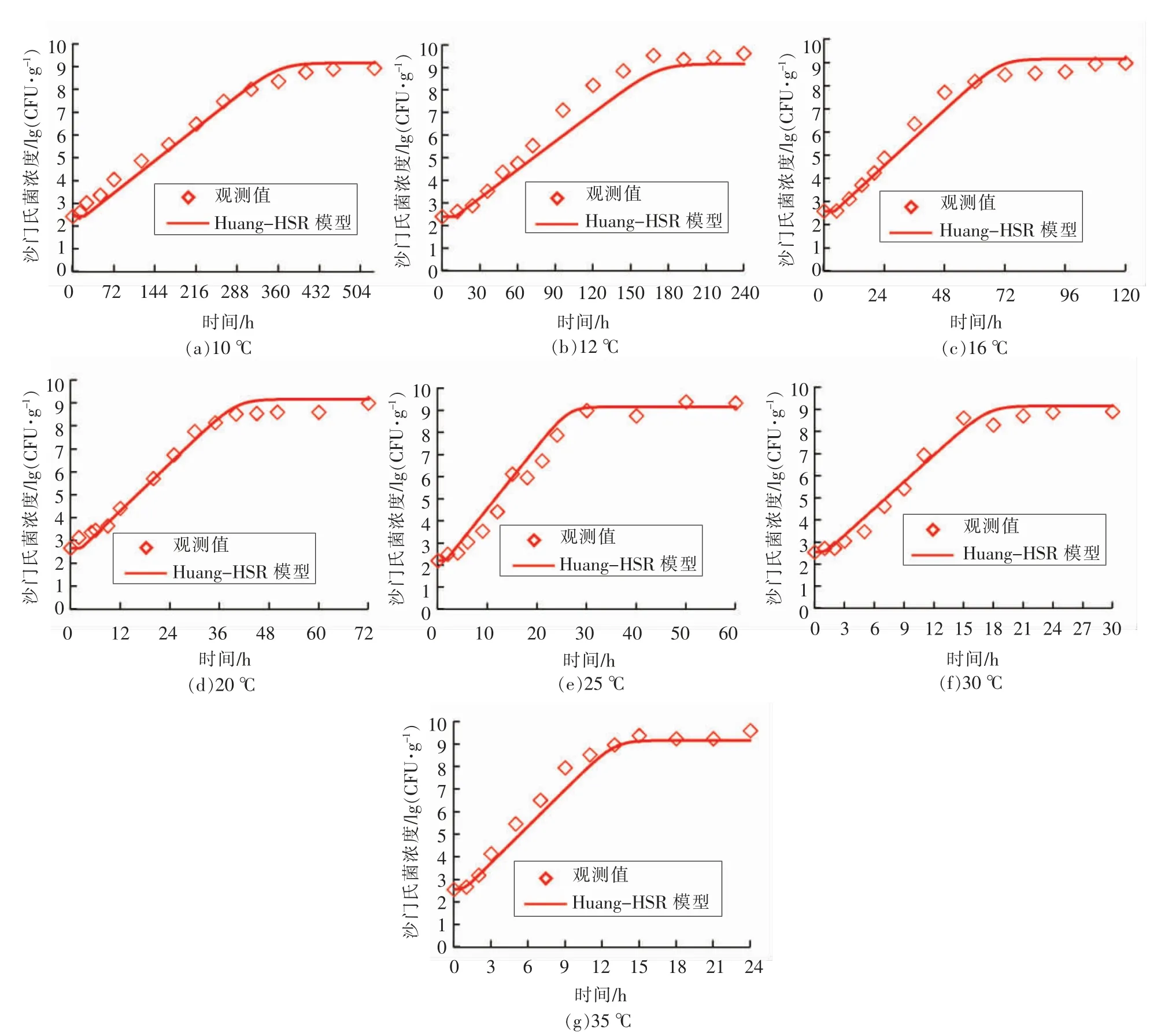
图3 模型验证：恒定温度条件下金枪鱼生鱼片中沙门氏菌的生长曲线Fig.3 Model validation：growth curves of Salmonella in tuna sashimi at isothermal condition

图4 恒定温度验证试验预测曲线误差[单位lg（CFU/g）]拟合分布Fig.4 The distribution of residual errors[in lg（CFU/g）]of prediction of isothermal validation

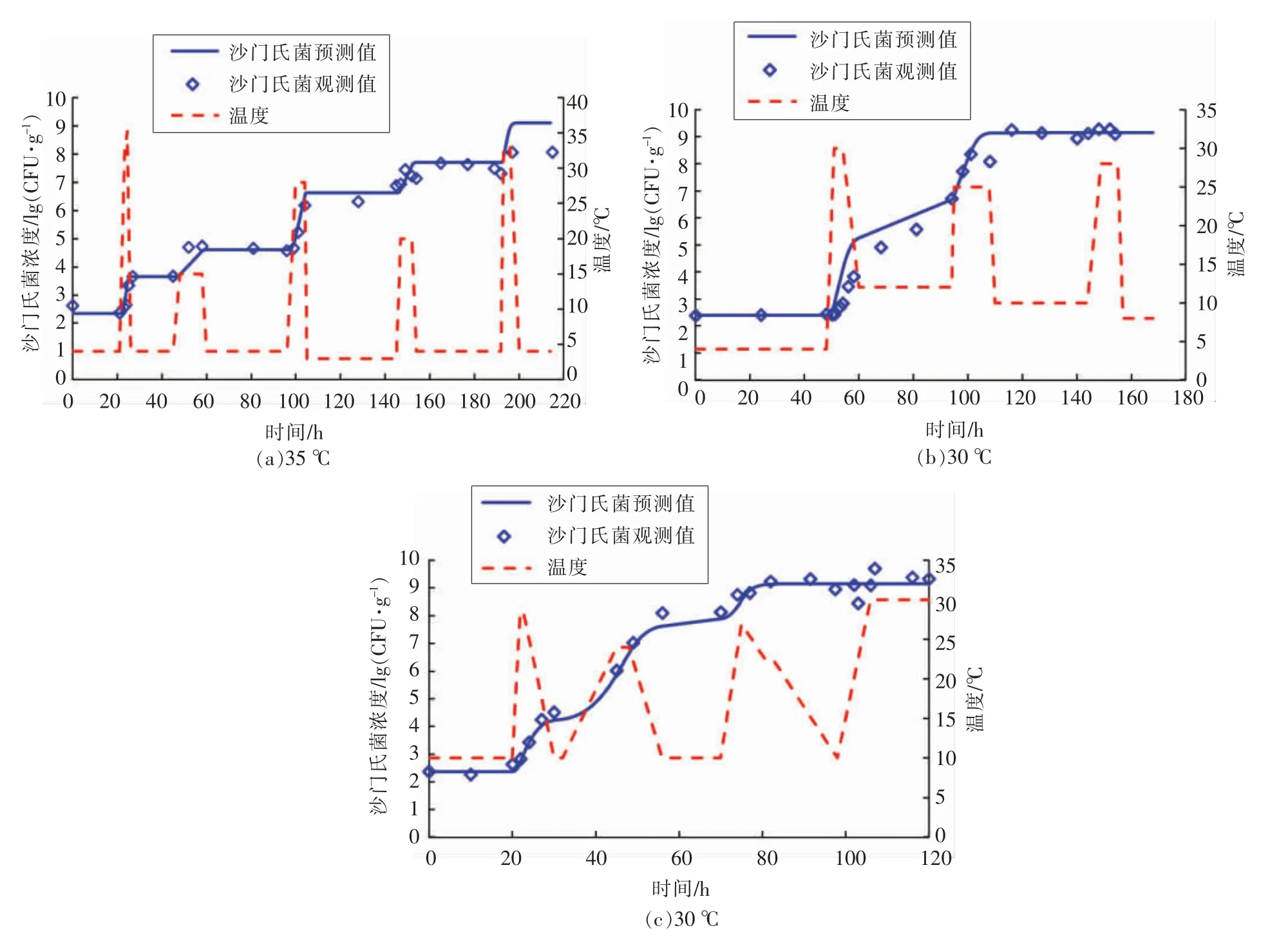
图5 模型验证：波动温度条件下金枪鱼生鱼片中沙门氏菌的生长曲线Fig.5 Model validation：growth curves of Salmonella in tuna sashimi at dynamic condition

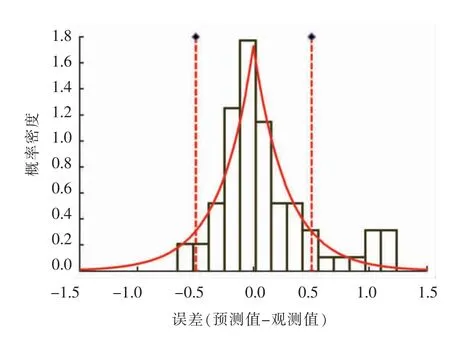
图6 波动温度验证试验预测曲线误差[单位lg（CFU/g）]拟合分布Fig.6 The distribution of residual errors[in lg（CFU/g）]of prediction of dynamic validation

3 结论

本研究考察不同恒定温度（8～35 ℃）条件下沙门氏菌在金枪鱼生鱼片中的生长特性，除8 ℃外，10～35 ℃条件下沙门氏菌的生长曲线均呈现出迟滞期、对数期及稳定期3 个阶段；一步法适用于金枪鱼生鱼片中沙门氏菌的生长曲线分析，Huang-HSR 模型与Barsnyi-HSR 模型对生鱼片中沙门氏菌的生长具有同等的拟合效果，由于Huang 模型对迟滞期的定义更为明确，建议选用Huang-HSR 模型；一步法分析估计的沙门氏菌的最低生长温度为6.91 ℃，最大生长浓度为21.08 ln（CFU/g）或9.15 lg（CFU/g）；恒定温度和波动温度验证试验的实测值与预测值相接近，其总均方根误差（RMSE）分别为0.37 lg（CFU/g）和0.44 lg（CFU/g）。综上所述，本研究表明一步法是同步构建初级模型和二级模型的有效分析方法，所构建预测模型可用于金枪鱼生鱼片中沙门氏菌的生长预测和风险评估。