高中数学几何解题中数形结合技巧探究
■刘亚静
高中数学课程中几何题是常见的题型,同时也是数学学习中的难点,同学们应当有效掌握数学学习技巧,相应地降低解题难度,从而缓解学习过程中的压力。下面主要针对常见的数学几何问题,提出数形结合的解题思路。
一、高中数学几何解题中数形结合应用的目的
第一,在解答高中数学几何问题的过程中,同学们应将数形结合思想应用于解题环节,从而提高解题效率。
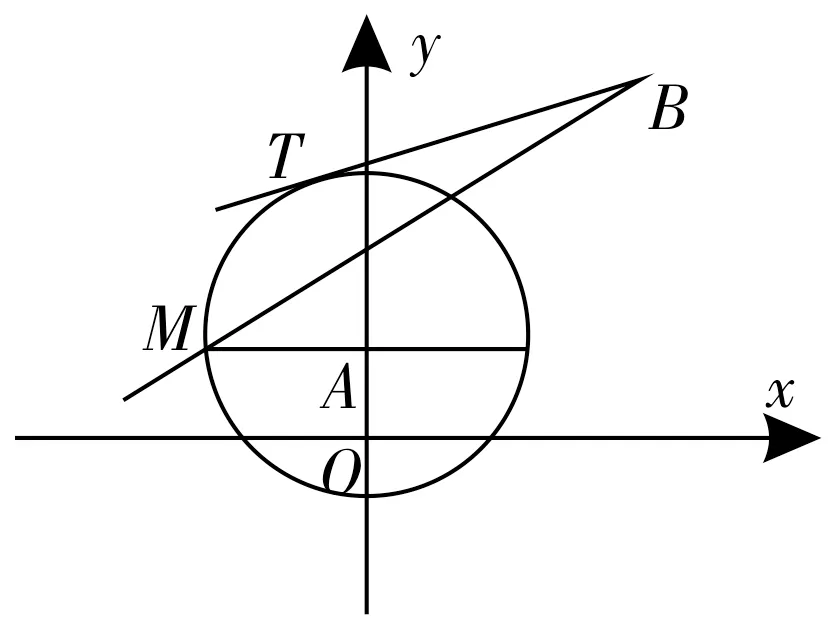
图1
第二,做题过程中应当有效利用数形结合思想,从数形结合的角度找寻解题的突破口,有效转化几何题的解决思路,明确解题技巧,以达到快速解答问题的目的。
第三,通过使用数形结合思想,可以促使同学们总结解题方法,掌握解题技巧,从而避免出现偏离正确答案等诸多问题,确保解题结果的正确性。
二、高中数学几何解题中数形结合应用的技巧
第一,通过形转数的方式掌握解答技巧。在数学解题过程中有效利用图像完成几何问题的解答,会使逻辑推理更为高效、准确。同时还可以通过数形结合这一有效的思想方法,校对答案是否正确,真正实现图形与数据的有效转化。

图2
例如,在解答不等式相关问题时,就要运用数形结合的方式,通过此方法提高问题的解决效率。如不等式(x-1)2<logax,x∈(1,2)恒成立,求实数a的取值范围。结合题中所给条件,可以画出图2,实现数字与图形的有效转化。经过上述分析后,同学们会发现解决不等式问题的过程中,有效利用数形结合的解题技巧,可将图形转化为数字,使得问题的解决更为高效、更为顺畅,并相应地提高问题解答的准确性。
第二,提高数形结合应用意识。同学们在学习高中数学时,要意识到数形结合解题应用的重要性,掌握数形结合的解题方法,以便更好地解答问题,提高解题的正确性。
例如,如图3所示,在△ABC中,∠BAC=45°,AD⊥BC,D为垂足,BD=6,CD=4,求△ABC的面积。如图3所示,作△ABD、△ACD关于AB、AC的对称图形△ABE、△ACF,连接FC与EB,并将其延长,交于点G,此时∠BAC=45°,AD为高线,可以证得AEGF为边长是AD的正方形。设AE=AD=x,此时在△BCG中,BG=x-6,CG=x-4,BC=10,最终可得。

图3
综上所述,同学们在学习数学几何知识的过程中,要有效利用数形结合的思想,不断总结解题技巧,及时发现规律,提高自主探究意识,真正将数形结合理念灵活应用在解题中,从而大大提高数学几何题的解题效率和正确性。

