隐私保护频繁项集挖掘中的分组随机化模型
郭宇红, 童云海
(1. 国际关系学院 信息科技学院, 北京 100091;2. 北京大学 智能科学系, 北京 100871)
数据挖掘能从大量数据中发现新颖的、潜在有用的、可被用户理解的知识,成为一种有效的分析决策手段,在企事业中得到广泛应用.频繁项集挖掘是数据挖掘中的一个重要分支,能从大量数据中发现有趣的关联关系.有效的数据分析需要有大量真实的数据做基础,而人们对数据隐私和安全问题的日益关注,使得在数据收集阶段中,出于隐私的考虑,人们可能不再愿意提供真实的数据供分析使用.因此,如何在基于隐私和安全考虑的环境中,很好地实施数据挖掘任务和各种应用,是隐私保护数据挖掘要解决的问题[1-3].
随机化[4-5]是目前隐私保护数据挖掘中运用的主要方法,基本思想是通过向原始数据中加入噪音的方式来对数据作干扰以达到隐私信息的保护,同时数据的统计性质在随机干扰后的数据中保持不变,以获取正确的挖掘结果,包括随机化干扰和随机化回答两种模型.其中,随机化干扰模型主要用于数值数据,通过在原始数值数据上增加随机干扰数实现;随机化回答模型主要用于分类数据,通过对分类属性值在不同取值间作随机变换实现,该模型最先由沃纳提出[6],被广泛用于敏感性问题的调查中.在隐私保护频繁模式挖掘[7-11]、隐私保护关联规则挖掘[12-14]的应用方面,文献[14]通过数据干扰和支持度重构实现了隐私数据保护的关联规则挖掘;文献[15]对MASK(mining associations with secrecy Konstraints)算法进行了扩展,提出“特定于符号(1和0)”的随机化过程和相应的eMASK算法;文献[16]提出“非统一”参数的随机化过程和相应的项集支持度递归估计RE(recursive estimation)算法;文献[17]对MASK算法在支持度重构复杂度方面进行了优化,提出了mMASK算法.
上述随机化回答模型在隐私保护频繁项集挖掘中取得很大进展,但存在以下2点问题.1) 随机化模型类型单一,随机化参数调控的数据范围宽、粒度粗,对隐私数据保护粒度的控制缺乏灵活性.2) 已有模型没有考虑不同个体隐私保护需求的差异性,而这种需求在现实应用中是客观存在和急需解决的.针对以上问题,本文在沃纳模型、单参数等随机化模型的基础上,提出个体分组多参随机化模型PN/g,并结合例子对水平分组随机化的支持度重构方法进行了探索.
1 沃纳模型
沃纳模型是最初由Warner在1965年针对“吸毒问题的调查”一类敏感问题提出的,可应用于单一属性敏感性问题的统计学调查和分析.在“吸毒问题的调查”这类问题中,调查者想要知道一定人群中吸毒者的比例,但当面对“你是否曾经吸过毒”这类敏感问题的回答时,被调查者(尤其是吸毒者)很可能不愿意回答,或者给出一个虚假的回答.针对这类问题,沃纳模型给出了解决办法.
该模型在调查中设计下面两个对立的问题供被调查者回答:1) 你是否吸过毒;2) 你是否没吸过毒.同时,分给每个被调查者一个随机数生成装置,被调查者可根据生成的随机数的不同,选择回答第1个问题,还是第2个问题.比如调查者可以跟被调查者事先约定:当生成的随机数小于p时,选第1个问题回答;大于等于p时,选第2个问题回答;无论选哪个问题,都要作出真实的回答.


(1)
2 单参数随机化模型
现有隐私保护数据挖掘方法所使用的随机化回答技术,是在沃纳模型的基础上形成的.沃纳模型只能用于单一敏感性问题的调查和分析,其核心思想是在保护个体数据隐私的同时,能求得单一属性上的统计值.对于频繁模式挖掘而言,其对应的数据通常会有多个属性项,频繁模式挖掘的目标则是通过对项集支持度的计算,发现在总体样本中所占比例较高的项集(即频繁项集).因此,对隐私保护频繁模式挖掘,其目标是在保护个体隐私的同时,求取多属性上的统计值——项集支持度.沃纳模型中的公式只能解决隐私保护场景下1-项集支持度的计算.文献[14]提出的MASK方法解决了隐私保护场景下k-项集的支持度计算问题,从而很好地解决了隐私保护频繁模式挖掘问题,其原理如下.
1) 随机化过程.假定用二维0-1矩阵表示原始事务集D,“1”和“0”分别表示对应的项出现和不出现在事务中,则单参数随机化对于D中任意元素v∈{0,1},以p的概率取原值v,以1-p的概率取1-v,生成随机化事务集D′.p称作随机化参数,p值越高,生成的D′中保留越多的原值v.
2) 支持度重构.假定A={I1,I2,…,Ik}为k-项集,A中的项可能全部或部分出现在D的事务T中.A∩T共有2k种可能的取值,每一种取值对应了A的一个子集fi(i∈{0,1,…,2k-1}),并假设在二维0-1矩阵表示D时,i的k位二进制数字恰好对应fi的从I1到Ik的k项0-1序列.即
同时,假定Cfi,Afi表示D(I1…Ik)中仅包含fi而不包含补集Afi中的任何项的事务数(fi在D(I1…Ik)中的净计数).即D中对应A的k列0-1序列等于fi的事务数.当A在上下文中明确时,Cfi,Afi简记为Cfi.Cf0,Cf1,…,Cf2k-1(简记为C0,C1,…,C2k-1)构成向量CA,即CA=[C0,C1,…,C2k-1]T;相应地,C′f表示D′中仅包含f的事务数,向量C′A=[C′0,C′1,…,C′2k-1]T.则CA和C′A的期望值存在如下关系,即
E(C′A)=P·CA.
(2)
式(2)中:P=[pi,j]为随机化概率参数p构成的2k×2k变换矩阵,pi,j表示D中仅包含fi(fi⊆A)的事务(即对应的从I1到Ik的k项0-1序列恰好为i的k位二进制值的事务)转换成D′中仅包含fj(fj⊆A)的事务的概率.若i和j对应的k位二进制0-1串中值相同的位数为r,则pi,j=pr(1-p)k-r(0≤r≤k).为便于理解,给出单参数随机化中3-项集的变换概率矩阵,如表1所示.
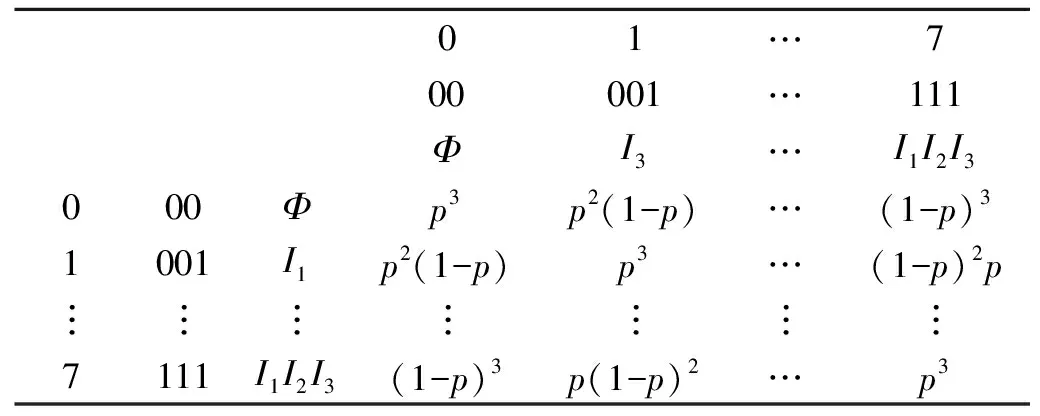
表1 单参数随机化中3-项集的变换概率矩阵Tab.1 Transition probability matrix of 3-itemset in single-parameter randomization
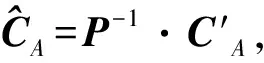
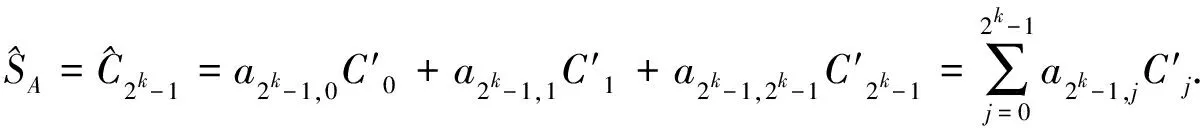
(3)
式(3)两边同除以事务总数∣D∣,可得MASK方法对项集A的重构支持度,即
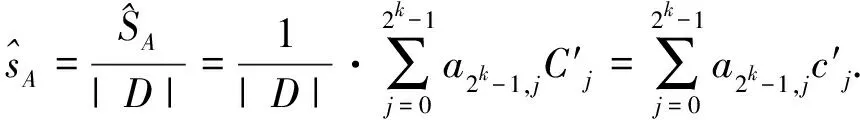
(4)
以上即为单参数随机化MASK方法在隐私保护频繁模式挖掘中的工作原理.该方法能保证在不访问原始数据D的情况下,从随机化后的数据集D′中估算出各项集的原始支持计数和支持度,从而得到频繁项集和关联规则挖掘结果.
单参数随机化模型的缺点是,所有数据元素的隐私保护程度和最终挖掘结果的准确性全都受控于单一的随机化参数p.这不仅忽视不同数据元素隐私保护需求的差异性,使隐私数据不能得到充分有效的保护,而且挖掘结果的准确性也不理想.挖掘结果受p的制约很大,p一旦确定,挖掘结果就确定,挖掘结果准确性上没有任何可调控的余地;而同时对隐私的保护也显得过于鲁棒、不够精准和粒度过粗.
3 分组多参随机化PN/g模型
3.1 PN/g基本思想
不同于单参数随机化,多参数随机化用多个概率参数对数据随机化.其思想是对数据中的不同元素设置不同的隐私保护级别,不同的隐私保护级别对应不同的随机化参数,由参与调查的个体自行决定对其不同数据元素的隐私保护级别和相应的随机化参数.参与调查的多个个体的隐私保护要求差不多,则可按个体水平分组随机化,使同一组内共用一个随机化参数,而每个随机化参数控制组中的多行.假设参与调查的个体总数为N,若等分时,每组包含g行,则组数和随机化参数个数为N/g,就形成分组多参随机化模型.
3.2 PN/g模型举例
为简单起见,假定属性取值均为布尔值“1”和“0”.由这N个个体的布尔属性组成需要保护的、二维布尔矩阵表示的数据表D.事实上,数值类型属性可以通过离散化转变为多元分类属性,即枚举属性,而多元分类属性又可以转变为布尔属性,即一般的数据都可以转变为二维布尔矩阵形式.
个体分组随机化的例子,如表2所示.表2中:TID为事务标识号;左边为原始事务集D,由10个被调查者的3个问题项(I1/I2/I3)组成,10个被调查者两两一组,同一组内共用同一个随机化参数.对这五组数据分别随机化后,生成的随机化数据集如表2右边3列数据所示.在表2中,由个体1和2构成的第1组数据选择的随机化概率参数p1=1,随机化过程对该组数据以1的概率保持为真,以0的概率取反,得到的第1组随机化数据完全保持不变.表明该组中的个体完全不顾及隐私,愿意完全真实地贡献其数据.相反的,由个体9和10构成的第5组数据选择的随机化参数p5=0.6,随机化过程对该组数据以0.6的概率保持为真,以0.4的概率取反,得到的第5组随机化数据中有3个值保持不变,3个值被打乱取反.表明该组中的个体相对比较在乎隐私,只肯贡献非常有限的数据.
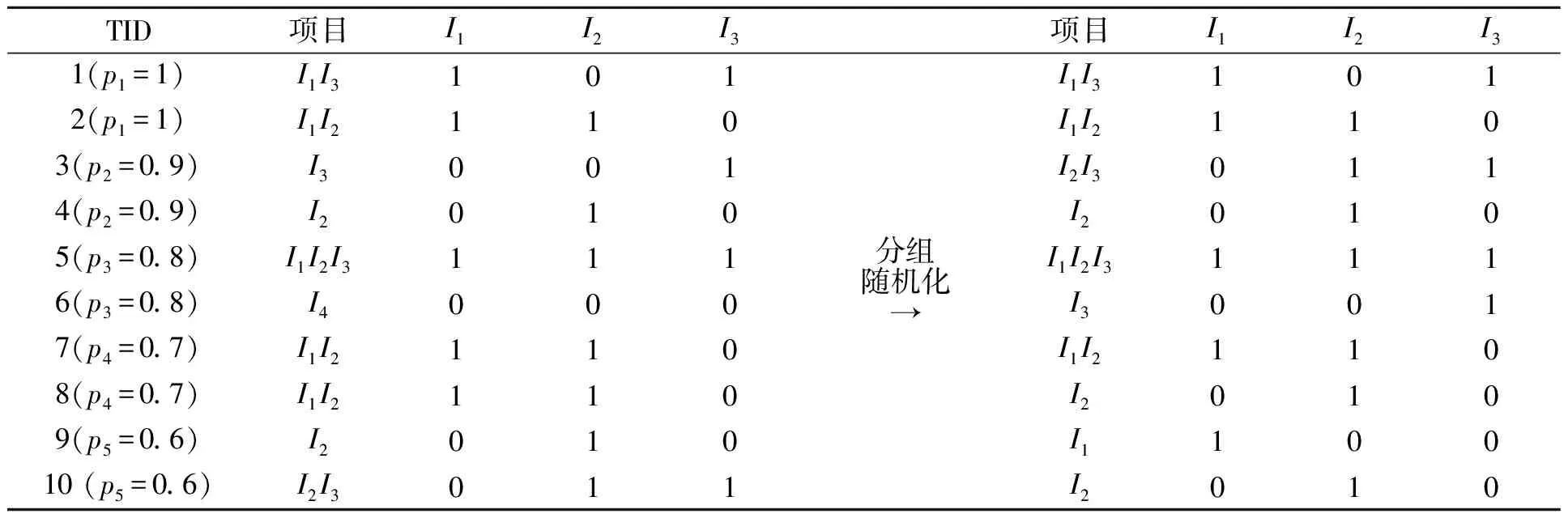
表2 数据集D分组随机化PN/g模型Tab.2 Grouping randomization model of PN/g on dataset D
3.3 PN/g模型支持度重构
分组多参随机化时,需要求得变换概率矩阵P和进行支持度重构.文中计算P中元素pi,j的基本思想是:D分组随机化为D′作为整体来看时,项集fi转变为fj的概率为各个分组将项集fi转变为fj的概率之和.相应地,k-项集A对应的2k×2k变换概率矩阵Pk中的元素值为
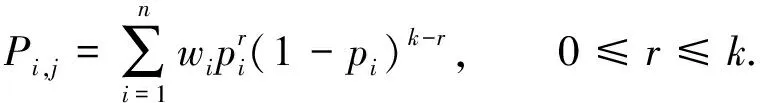
(5)

例如表2中的分组多参随机化中,事务“000”转变“000”的概率为
而“000”转变为“111”(即空集转变为事务{I1I2I3})的概率为
这样便可得到3-项集{I1I2I3}对应的8×8变换概率矩阵P3中的所有元素.
分组随机化PN/g模型变换概率矩阵P3,如表3所示.表3中:矩阵P3中的某一元素表示某个项集随机化后转变为另一个项集的概率.

表3 分组随机化PN/g模型变换概率矩阵P3Tab.3 Transition probability matrix P3 in grouping randomization of PN/g model
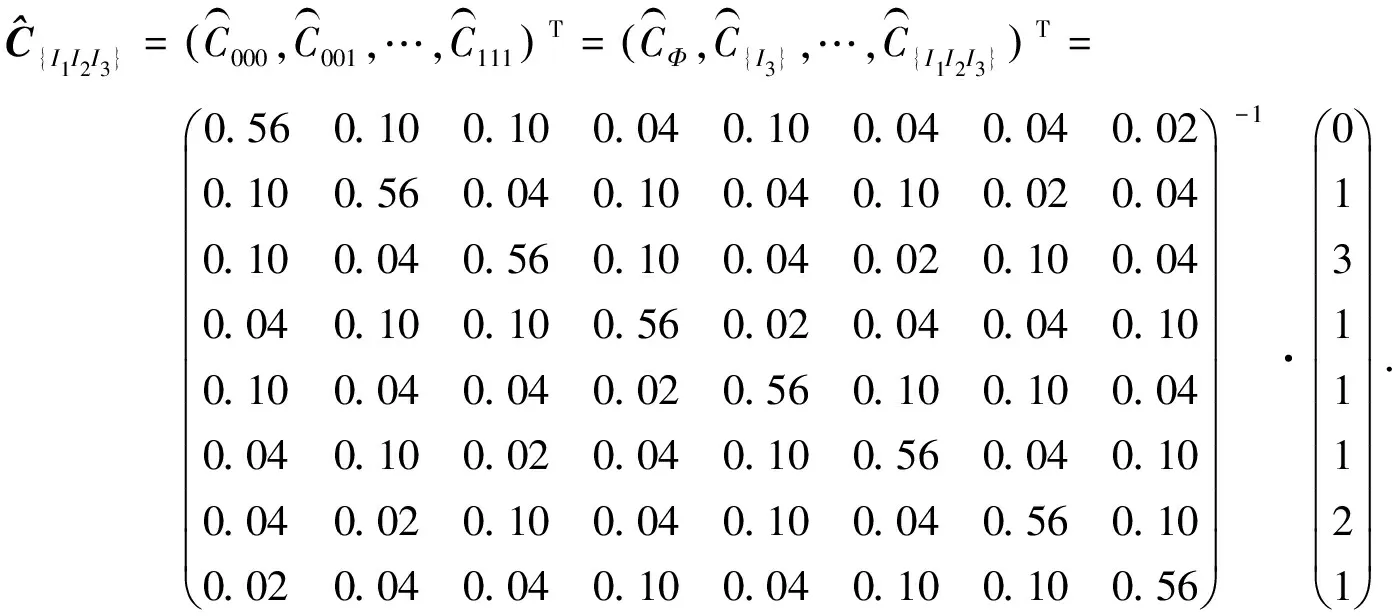
(6)
3.4 PN/g模型支持度重构示例分析
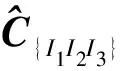
表4给出了表2数据集D对应的项集空间中,所有项集的重构支持计数和重构误差.从表4可看出:7个项集支持计数重构总误差为-1.92,平均每个项集的支持计数重构误差为-0.27.即相对原数据,每个项集支持计数估计值比真实值少了0.27.该误差较小,验证了文中所提PN/g模型支持度重构方法的可行性和有效性.

表4 PN/g和MASK支持计数重构对比Tab.4 Support count reconstruction comparison of PN/g and MASK
3.5 与MASK方法对比

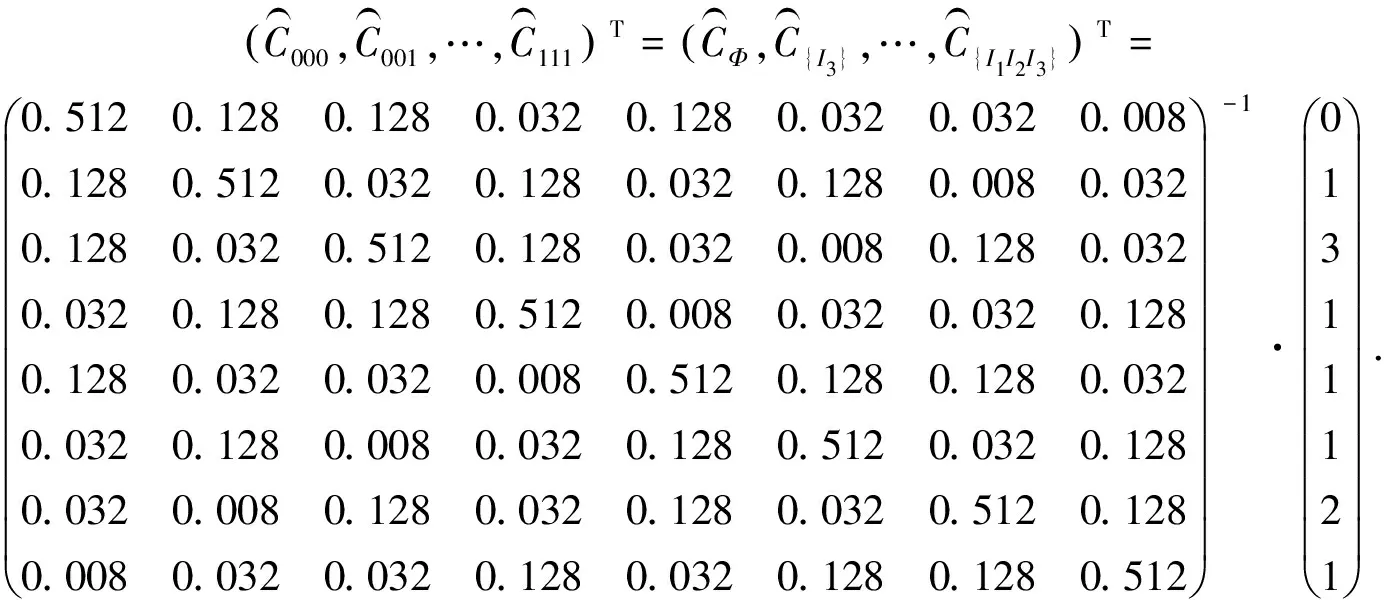
(7)
对比原始支持计数发现,相对于文中所提PN/g模型,MASK方法仅在支持计数低的项集I1I2I3上,重构支持计数误差绝对值(0.26)更小,而在支持计数相对高的其他项集上,PN/g模型的重构误差绝对值小于或等于MASK,这意味着对频繁项集挖掘,PN/g模型在频繁项集的支持度重构上将更为准确.由表4可知:整个项集空间支持计数重构的总误差和平均误差绝对值也小于MASK.这进一步验证了文中所提PN/g模型用于隐私保护频繁项集挖掘的有效性,即PN/g模型不仅能实现差异化的隐私保护,且能以小的误差重构频繁项集的支持度.同时,相对单参数随机化MASK,多参数随机化PN/g模型能在平均隐私保护度相同情况下,以更小的误差重构频繁项集的支持度,从而提高频繁项集挖掘的准确性.
4 结论
针对频繁项集挖掘中的隐私保护问题,提出个体分组多参随机化PN/g模型,给出其在隐私保护频繁项集挖掘中的支持度重构方法.最后,通过示例验证了支持度重构方法的可行性和有效性.
作为个性化隐私保护挖掘的初步尝试,还有如下一些工作需要进一步探究.1) 针对PN/g模型的支持度重构方法,理论推导出该方法所对应的支持计数重构公式和支持度重构偏差公式.2) 设计相应算法和基于大数据集进一步验证方法的有效性,特别是挖掘结果的准确性.3) 基于新的频繁项集挖掘算法[18],设计与之相适应的、更高效的隐私保护频繁项集挖掘算法.

