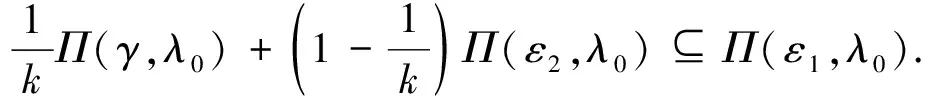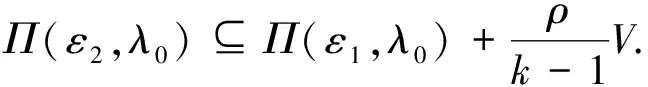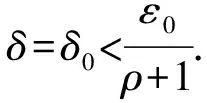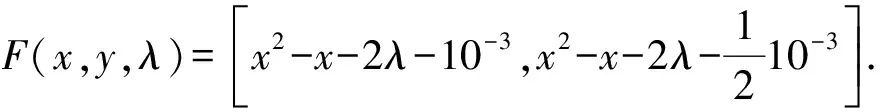集值向量均衡问题近似解映射的连续性
陈斌, 王浩智
(华侨大学 数学科学学院, 福建 泉州 362021)
均衡问题[1]为许多优化有关的重要问题提供了统一框架,如极值问题、变分不等式、互补问题、纳什均衡、极大极小问题、不动点问题,以及交通网络等.在过去的20年,均衡问题解及近似解的存在性条件已被广泛研究[2-8].另一个重要的课题是研究均衡问题解及近似解的稳定性和敏感性分析.目前,有很多学者研究了解及近似解的(半)连续和Hölder连续性[9-15].为了获得解或近似解的(半)连续性,许多文献利用了映射的单调性或者解映射的信息.其中,映射的单调性可能导致整个解集是单点集.此外,假设条件中涉及解映射的信息是不合理的,在实践中很难实现.当处理含参向量均衡问题解映射的(半)连续性时,许多文献利用了标量化方法.然而,这一方法只有对含参弱向量均衡问题有效,对强向量均衡问题则不适用.文献[16]在未使用标量化方法的情况下,建立了强向量均衡问题和对偶强向量均衡问题近似解映射的Hausdorff上下半连续性的充分条件,改进了已有文献中的相关结果.
本文主要研究局部凸Hausdorff拓扑向量空间中扰动下的集值向量均衡问题的原问题和对偶问题,建立其近似解映射的Hausdorff上下半连续性的充分条件,改进和推广了文献[16]的已有结果.
1 预备知识
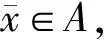
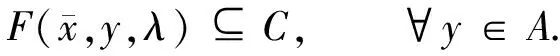
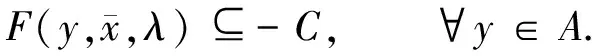
令e∈intC.对于(ε,λ)∈R+×Λ,设SVEP和DSVEP的ε-近似解集分别为
Π(ε,λ)={x∈A|F(x,y,λ)+εe⊆C,∀y∈A},
Πd(ε,λ)={x∈A|F(y,x,λ)+εe⊆-C,∀y∈A}.
以下先给出一些基本概念和引理.
设F为X到Y的集值映射.
定义1[17]ⅰ) 若对于Y中任意满足F(x0)⊆U的开子集U,都存在x0的一个邻域N,使F(N)⊆U,则称F在x0处上半连续.
ⅱ) 若Y中满足F(x0)∩U≠Ø的任意开子集U,都存在一个x0的邻域N,使得对于所有的x∈N,都有F(x)∩U≠Ø,则称F在x0处下半连续.
ⅲ) 若F在x0处同时为上半连续和下半连续,则称F在x0处连续.
引理1[18]F在x0处是下半连续的,当且仅当对于y0∈F(x0)及所有xα→x0,存在ya∈F(xα),使得yα→y0.
定义2[18]ⅰ)F在x0处称为Hausdorff上半连续,如果对于Y中原点的任意邻域V,都存在x0的邻域N,使得
F(x)⊆F(x0)+V, ∀x∈N.
ⅱ)F在x0处称为Hausdorff下半连续,如果对于Y中原点的任意邻域V,都存在x0的邻域N,则使得
F(x0)⊆F(x)+V, ∀x∈N.
ⅲ) 如果F在x0处同时为Hausdorff上半连续和Hausdorff下半连续,则F在x0处称为Hausdorff连续.
引理2[18]ⅰ) 如果F在x0处是上半连续,那么F在x0处是Hausdorff上半连续;反之,如果F在x0处是Hausdorff上半连续,且F(x0)是紧集,那么F在x0处是上半连续.
ⅱ) 如果F在x0处为Hausdorff下半连续,则F在x0处为下半连续;反之,如果F在x0处是下半连续,且F(x0)是紧集,那么F在x0处是Hausdorff下半连续.
定义3如果对于任意ε>0,存在λ0的邻域N,使得对于所有x,y∈A和λ1,λ2∈N,都有
F(x,y,λ1)⊆F(x,y,λ2)+ε[-e,e],
则称集值映射F:A×A×Λ→2Y关于e∈intC在λ0处对于(x,y)∈A×A一致连续,其中,[-e,e]∶={x∈Y|x∈(e-C)∩(-e+C)}.
定义4[18]如果对于任意x1,x2∈A和t∈[0,1],有
F(tx1+(1-t)x2)⊆tF(x1)+(1-t)F(x2)+C,
(1)
则称映射F:X→2Y在凸集A⊆X上是C-凹的.
如果将式(1)替换为
F(tx1+(1-t)x2)⊆tF(x1)+(1+t)F(x2)-C,
则称映射F:X→2Y在凸集A⊆X上是C-凸的.
对于固定的λ0∈Λ,可以得到以下结果.
引理3如果对于任意y∈A,F(·,y,λ0)在凸集A上是C-凹的,那么Π(ε,λ0)是凸集.
证明:任取x1,x2∈Π(ε,λ0)⊂A和t∈[0,1],那么tx1+(1-t)x2∈A,且对于所有y∈A,有
利用F的C-凹性,对于所有y∈A,有
F(tx1+(1-t)x2,y,λ0)+εe⊆tF(x1,y,λ0)+(1-t)F(x2,y,λ0)+εe+C⊆
t[F(x1,y,λ0)+εe]+(1-t)[F(x2,y,λ0)+εe]+C⊆C,
即tx1+(1-t)x2∈Π(ε,λ0),从而Π(ε,λ0)是凸集.
2 主要定理和结果
由于已有文献对精确解和近似解的存在性进行了深入研究,因此总是假定近似解集在参考点(ε0,λ0)附近是非空的.
定理1对于SVEP,假设在参考点(ε0,λ0)∈R+×Λ的邻域内近似解存在,且
ⅰ)F(x,y,·)关于e∈intC在λ0处对于(x,y)∈A×A一致连续;
ⅱ) 对于所有y∈A,F(·,y,λ0)在凸集A上是C-凹的.
那么,Π在(ε0,λ0)处是Hausdorff连续的.
证明:令δ∈(0,ε0),取集合N=(ε0-δ,ε0+δ)作为给定的ε0的邻域.任取ε1,ε2∈N,其中ε1<ε2,实数η满足0<η<ε2-ε1,由定理1的假设条件ⅰ)可知,存在λ0的邻域Nη(λ0),使得对于任意的λ1,λ2∈Nη(λ0)和x,y∈A有
F(x,y,λ2)⊆F(x,y,λ1)+η[-e,e].
(2)
对于任意的λ1,λ2∈Nη(λ0),下证
Π(ε1,λ1)⊆Π(ε2,λ2).
(3)
设x∈Π(ε1,λ1),则对于所有y∈A,有
F(x,y,λ1)+ε1e⊆C.
任取z2∈F(x,y,λ2),由式(2)存在z1∈F(x,y,λ1)及c1∈C,使得z2=z1+η(-e+c1).从而有
z2+ε2e=z1+ε1e+(ε2-ε1)e-ηe+ηc1=z1+ε1e+(ε2-ε1-η)e+ηc1⊆C,
则F(x,y,λ2)+ε2e⊆C,∀y∈A,即x∈Π(ε2,λ2).
由式(3)可知,对于任意的λ∈Nη(λ0)和ε∈N,有
Π(ε0-δ,λ0)⊆Π(ε,λ)⊆Π(ε0+δ,λ0).
(4)
对于满足1 下证 (5) 任取x1∈Π(γ,λ0),x2∈Π(ε2,λ0).由A的凸性可知k-1x1+(1-k-1)x2∈A,且对于所有y∈A,有 F(x1,y,λ0)+γe⊆C,F(x2,y,λ0)+ε2e⊆C. 因此,有 利用F的C-凹性,对于任意的y∈A,有 即 k-1x1+(1-k-1)x2∈Π(ε1,λ0). 由此可得到式(5),并由式(5)可得到 则有 由于A是紧集,故它是有界的.因此,对于X中原点的任意闭凸邻域V,存在ρ>0,使得A-A⊆ρV.因此有 (6) Π(ε0,λ0)⊆Π(ε0-δ0,λ0)+V⊆Π(ε,λ)+V. 故Π在(ε0,λ0)处是Hausdorff下半连续. 在式(6)中,取ε1=ε0,ε2=ε0+δ0,k=ρ+1,可得到 Π(ε0+δ0,λ0)⊆Π(ε0,λ0)+V. 结合式(4),可得出Π(ε,λ)⊆Π(ε0,λ0)+V,即Π在(ε0,λ0)处是Hausdorff上半连续. 注1当F为单值映射时,就得到了文献[16]的定理1,定理1推广了文献[16]的定理1. 注2定理1的假设条件ⅱ)是必不可少的,如下例所示. 但由于 显然有 因此,F的C-凹性条件不满足. 近似解映射Π在(10-3,0)处不是Hausdorff连续的. 因为0∈ 注3当F退化为单值映射时,上例改进了文献[16]中的例1. 注4约束集的紧性条件不能删除,如下例所示. 例2令X=R,Λ=[0,1],A=(2,3],Y=R,C=R+,e=1∈intC,ε0=10-3,λ0=0,且F(x,y,λ)=[λ(x-y),λ(x-y)+1].易知满足定理1的假设.通过计算可以得到 Π在(10-3,0)处非下半连续,由引理2可知,近似解映射Π在(10-3,0)处不是Hausdorff连续的. 与定理1的证明类似,可以得到集值向量均衡问题的对偶问题近似解映射Hausdorff连续性的充分性条件. 定理2对于DSVEP,假设在参考点(ε0,λ0)∈R+×Λ的邻域内近似解存在,且ⅰ)F(y,x,·)关于e∈intC在λ0处对于(y,x)∈A×A一致连续;ⅱ) 对于所有y∈A,F(y,·,λ0)在凸集A上是C-凸的.那么,Πd在(ε0,λ0)是Hausdorff连续的.