插电式混合动力汽车的燃油经济性优化分析

陈亚伟， 邵毅明， 程前

(1. 中国汽车工程研究院股份有限公司， 重庆 401147；2. 重庆交通大学 交通运输学院， 重庆 400074)

采用生态驾驶(节能或经济驾驶)是提高汽车燃油经济性的有效途径.先进驾驶辅助系统(ADAS)的发展，使生态驾驶与交通行程数据的结合成为现实.将生态驾驶作为一个最优控制问题(OCP)，在交通约束的前提下，通过对车速的控制，可以减少燃油消耗，这比仅对动力系统进行优化更能减少燃油消耗[1-3].近年来，针对混合动力汽车的能量管理与生态驾驶的研究日益增多.文献[4-7]指出，在有限交通预测的假设下，可以通过仅使用由行驶过程中分开的两个阶段来表示最佳轨迹；然后，应用两阶段Pontryagin的最值原理(PMP)分析推导出最优控制器的求解公式.文献[8-10]提出一种具有不同更新频率和预测步长的3层预测控制方案，顶层计算凸优化问题中的动能和电能，对应的双变量作为状态参考和燃油消耗，通过求解瞬时优化的等效消耗最小化策略(ECMS)，在实时决策层中以自适应的方式应用到控制系统中.文献[11-13]将混合动力汽车的能量管理问题分为长预测层荷电状态(SOC)规划和短层速度与SOC规划相结合进行能量管理优化控制.

目前，虽然已经提出了较多的混合动力汽车的控制策略，但是插电式混合动力电动汽车的速度和充电损耗的协同优化仍是一大难题.这是因为对于插电式混合动力汽车(PHEV)来说，电池荷SOC具有宽范围(通常在10%～90%之间)，增加了自由度，且难以选择最佳参考值[14].针对上述问题，本文首先通过最小化加速度和制动来平滑车速，然后在所得到的平滑速度曲线上对发动机和电动机之间的功率进行分配，以最小化燃料消耗.

1 控制模型的建立

1.1 车辆跟随子系统

将车速和位置描述为速度优化问题的质点系统，即

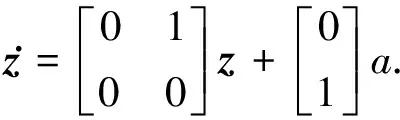
(1)

式(1)中：z=[s，v]T，s，v分别表示车辆的位置和速度；a是车辆的加速度.

根据车辆制动和加速极限要求，加速度极限为amin(t)≤a(t)≤amax(t)，t为发动机工作时长.根据各路段限速，车速受vmin(t)≤v(t)≤vmax(t)的约束,同时，车辆的位置也受到交通状况及前车的制约.在任何时候，车辆应具有安全合理的车距，因此有smin(t)≤s(t)≤smax(t).

假设目标车辆的加速度a和速度v的约束条件在优化计算将要执行的时间范围内是不变的.由于目标车辆的位置取决于其先前车辆的位置sL和速度vL,且受到时变约束，因此设置状态约束[15]为

(2)

式(2)中：L为车长,L=4.5 m；d为横向车距，最大横向车距dmax=3 m,最小横向车距dmin=1.2 m.

1.2 混合动力子系统

电池荷电状态是PHEV电池耗散优化的主要状态，其值主要取决于电池功率Pbatt,即

(3)

式(3)中：Voc，Rbatt，Cbatt分别为电池的开路电压、内阻和额定电量；PMG1和PMG2分别为发电机和电动机的功率[16]，有

PMG1=TMG1·ωMG1+PMG1,loss,PMG2=TMG2·ωMG2+PMG2,loss.

(4)

式(4)中：TMG1，ωMG1分别为发动机的扭矩和转速；TMG2，ωMG2分别为电动机的扭矩和转速；PMG1，loss和PMG2，loss分别为发电机和电动机的功率损耗，相关参数可查询.给定车速v，电动机转速ωMG2=vK1/Rtire,其中，Rtire为轮胎半径；K1为最终传动比.

根据驱动条件可知，驱动扭矩Tdriver满足

Tdriver=Tout-Tf,Tf≥0.

(5)

式(5)中:Tf为摩擦阻力矩;Tout为动力系统输出扭矩.

(6)

式(6)中:meff，m，Af分别为车辆的等效质量、实际质量和迎风面积；Cf为滚动阻力系数；Cd为空气阻力系数；ρ为空气密度；θ为路面坡度，假设θ为已知量且下坡为正；g为重力加速度.

发电机、电动机和发动机的速度由动力分配装置(PSD，行星齿轮组)耦合得到，即

ωMG1S+ωMG2K2R=ωe(R+S).

(7)

式(7)中:S和R分别为太阳齿轮和齿圈的半径；ωe为发动机转速；K2为电动机减速比.

发电机扭矩TMG1，电动机扭矩TMG2，发动机扭矩Te和离合器扭矩Tcl的耦合关系如下:1) 在混合动力汽车(HV)和电动汽车(EV)模式下，TMG1+F·S=0,Te-F·(R+S)=0；2) 在双电机驱动(DM)模式下，TMG1+F·S=0,Tcl-F·(R+S)=0.其中，F为不同齿轮之间的相互作用力.离合器扭矩Tcl传递齿轮反作用力F时,发动机停止工作，且发电机产生反向扭矩.

发动机扭矩Te和发电机扭矩TMG1通过反作用力F结合到齿圈扭矩Tr，即Tr=F·R.

在输出轴上，由齿圈传递的扭矩与电动机传递的扭矩之和为Tout，即Tout=(TMG2+K2Tr)K1.

考虑到实际行驶情况，设置约束条件[17]，有

(8)

2 顺序优化方法

2.1 基于交通约束的速度平滑

通过使加速度最小化来平滑速度，将连续时间车辆跟随子系统转化为离散时间系统，得到离散时间下的线性时不变系统为

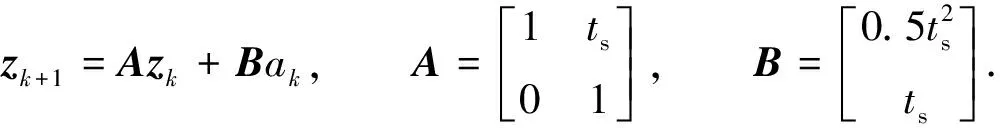
(9)

式(9)中：zk=[sk，vk]T为车辆状态;ak为时刻k的加速度；ts为采样时间；状态变量X=[zT1，zT2,…，zTN]，N为步长上限;控制输入变量U=[a0，a1,…，aN-1]T.由顺序控制输入U可以得到执行的最小化加速度值，该问题可以转化为多维约束优化问题.目标函数J1具有以下形式

(10)

式(10)中：D为约束向量；W为交通约束矢量；T为扭矩向量；z0=[s0，v0]T是车辆的初始位置和速度.控制约束可由状态约束得到，这是一个标准线性二次(LQR)最优控制问题，用Matlab二次规划(QP)求解器求解.

2.2 最低油耗问题的规划

在连续时间内，对最低油耗问题进行数学规划,则

(11)

式(11)中：J2为油耗函数；x=SOC;u=[ωe，Te]T;ω=[Tdriver，v]T.

该问题的哈密顿形式为

(12)

根据Pontryagin的最值原理(PMP)的必要条件，原始最优控制问题的解[8]需要满足

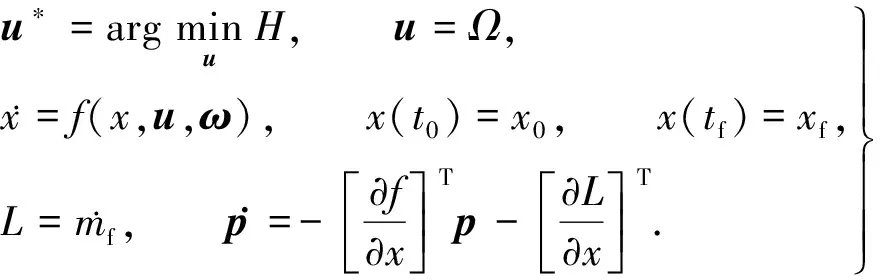
(13)

最后，对两点边值问题(TPBVP)进行数值求解.

3 控制器性能评价与分析

3.1 制定基线能量管理策略

1) 耗散电量(CD).强制系统在电动汽车(EV)模式下运行，此时Te=0，ωe=0，直到电池SOC低于指定的终端SOC值，车辆将立即进入混合动力汽车(HV)模式.车辆即将进入HV模式时刻的SOC值记为SOC(th).

2) 充电持续(CS).用SOC0=SOC(th)来制定剩余行程的最低油耗问题.车辆在HV模式下运行，其中,Te和ωe是通过优化算法确定的，这有助于实现剩余行程的最低油耗.在此期间，电池以与生产PHEV上的充电维持模式类似的方式辅助发动机.

3.2 两种组合行驶模式的评价

为了评估控制器的性能，通过组合3种典型的测试循环来创建不同的行驶模式，包括城市道路循环(UDDS)、公路燃油经济性测试(HWFET)和US06补充测试工况.选取两种场景作为两种极端情况，以此评价不同行驶模式的燃油经济性，两种组合行驶模式，如表1所示.

表1 两种组合行驶模式Tab.1 Two combined driving modes

1) 最差CDCS行程.此种工况下，CDCS策略在真实速度曲线上的结果远非最佳.该行程在开始时需要高功率，采用最佳耗散策略时，发动机一开始就会处于结合状态，这可以储存更多的电能以供后续行程使用.但因为最初的高功率需求，电能将很快耗尽，发动机必须在行程的其余部分进行接合，以保持最低SOC水平.

2) 最佳CDCS行程.此种工况下，CDCS策略在真实速度曲线上的结果接近最优.该行程开始时动力需求低且车速高，因此,系统首先使用电池中的电能，当高功率需求的行程结束时,再结合发动机.

最差CDCS行程总行程距离为107.62 km，行程时长为2 h 4 min 5 s.最佳CDCS行程总行程距离为124.12 km，行程时长为2 h 16 min 51 s.在这两种情况下，所述循环的总行程能量都超过了模拟车辆的可用电池能量，表明所提出的充电耗散策略具有一定的效果，可以节省燃油消耗.车辆仿真中设计的速度和能量管理策略，如表2所示.

表2 车辆仿真中设计的速度和能量管理策略Tab.2 Speed and energy management strategies designed in vehicle simulation

4 仿真结果分析

两种不同行驶模式的仿真结果，如图1所示.图1中：PD为驱动功率；G为燃油消耗质量.由图1可知：在最差CDCS行程中，速度和电能耗散顺序优化策略(SV-OCBD)的总油耗比实际速度曲线上的基线耗散策略(RV-CDCS)降低了13.74%；而在最佳CDCS行程中，相对于实际速度曲线上的基线耗散策略(RV-CDCS)，速度和电能耗散的顺序优化策略(SV-OCBD)总油耗降低了7.07%.

(a) 最差CDCS行程 (b) 最佳CDCS行程图1 两种不同行驶模式的仿真结果Fig.1 Simulation results of two different driving modes

在最差CDCS行程中，RV-OCBD策略相对于RV-CDCS策略有更好的效果，不仅使发动机在进入混合动力(HV)模式后在最高效点工作，而且在后续行程中仍持续输出动力.

不同情况下的燃料消耗、发动机启动时间和能耗结果,如表3所示.表3中：δ为燃油减少占比；QB为制动能量；QD为驱动能量；S为纯电动行驶里程.由表3可知：与RV-CDCS策略相比，RV-OCBD策略减少了发动机在中功率区域运行的总时间；与给出的最佳SOC耗散策略相比，基于实际速度的基线策略具有更长的发动机运行时间；然而，对于最佳的CDCS行程，在行程开始时的功率需求是中等负荷，而在行程结束时出现高功率需求，这不利于节省电能以增加续驶里程.因此，与RV-OCBD策略相比，在行程的后半段使用发动机的RV-CDCS策略是最优的.

表3 不同情况下的燃料消耗、发动机启动时间和能耗结果Tab.3 Fuel consumption， engine start time and energy consumption results under different conditions

最佳CDCS行程的仿真结果表明，平滑速度即使对电池充电的效率优化较低，也能显著提高插电式混合动力汽车的燃油经济性；同时，平滑的速度也有助于汽车的稳定性和舒适性.

5 结论

在给定交通约束条件下，对一种轻型插电式混合动力汽车(PHEV)的速度曲线顺序优化的方法及相应的充电损耗策略进行研究.为了评价该方法的有效性，给出并分析两种不同功率需求模式下的行程结果.仿真结果表明，混合动力汽车的燃油消耗有所下降，所设计的顺序控制策略具有一定的优越性.由此得到以下3点结论.

1) 平滑的速度策略显著降低了平均功率需求.行程开始时，较低的电能需求使在切换到表3的混合模式之前(使用CDCS)，可以行驶更长的里程.

2) 降低发动机驱动力比优化充电效率更能减小总的燃油消耗.即与RV-CDCS策略相比，SV-CDCS策略具有更好的节能性.

3) 速度平滑与电能损耗之间有耦合性.由于加速度最小化的控制方法减小了不必要的制动，SV情况下电池SOC的下降高于RV情况下电池SOC的下降.总的来说，SV减少了再生制动的机会，它避免了一些制动的操作和不必要的加速，因此，其节能效果更好.