剪切滑移裂缝中流体渗流的Lattice Boltzmann模拟研究

曲冠政　王一妃　林鑫　Randy Doly Hazlett　韩强　柏明星

摘要：针对目前学界有关剪切滑移作用对裂缝中流体渗流研究较少的情况，分析现有研究方法的缺陷，改进现有的研究模型，以固定研究目标尺寸为基础，引入Lattice Boltzmann方法，研究流体在剪切滑移结构中的渗流，并考察非匹配性和接触面积对流体渗流的影响。结果表明：随机二维剖面线可拆分为V型、正弦和凹槽等基本单元体;在基本单元体、二维剖面线中，裂缝面的滑移造成渗流方向上开度分布的非均匀性，渗透率呈现数量级的减小;非匹配情况下的裂缝渗透率比匹配情况下的低，随滑移距离的增加，流体渗流能力均呈先下降后上升趋势;三维裂缝结构的渗透率随滑移距离的增加总体呈下降趋势，下降幅度比基本单元体和二维剖面线结构要低;裂缝面产生剪切滑移时，结构间的非匹配性造成流体渗流轨迹呈三维迂曲性;剪切滑移所造成的非匹配性及接触面积，均对渗流能力有负面作用，但非匹配性可以对裂缝结构起到一定的自支撑作用。

关键词：剪切滑移;粗糙裂缝;Lattice Boltzmann模拟;渗流规律

中图分类号：TE357.4

DOI：10.16152/j.cnki.xdxbzr.2020－02－005

Study on fluid migration in the shear－slip fractureby Lattice Boltzmann simulation

QU Guanzheng1， WANG Yifei LIN Xin3，Randy Doly Hazlett4， HAN QiangBAI Mingxing1

Abstract： Considering that the research about the influence of shear－slipping on fluid transportation in fractures is few， the defect of current research methods is pointed out and the improvement is suggested， the method of keeping research object scale constant and Lattice Boltzmann method are employed to study fluid migration in shear－slipping fracture and the influence of mismatch and contact area are also included. The result shows that： The random 2D profile constitutes of V structure， sinusoid and groove structure; Morphogenesis makes aperture distribution heterogeneous along fluid seepage direction in basic units， and 2D profile， and the permeability shows tremendous decrease; The permeability of mismatch fracture is lower than it in match fracture; Moreover， as the slipping distance increases， the permeability firstly decreases， then increases. In 3D fracture structure， the permeability totally decreases as the slipping distance increases， and the decline range is lower than that in basic units and 2D profile. When the slipping occurs， the mismatch between fracture surfaces makes the fluid immigration path 3D circuitously; The mismatch and contact area， caused by shear slip， are negative for fluid immigration， but the mismatch could make the fracture structure self－supporting.

Key words： shear－slipping; rough fracture; Lattice Boltzmann simulation; seepage rule

體积化裂缝网络改造技术是目前开发页岩、致密砂岩等非常规储层的主要手段。区别于常规低渗透层的压裂改造方式，体积化压裂改造措施充分利用了储层的三维空间，尽可能地将储层打碎，形成低流阻裂缝网络结构［1-4］。低流阻裂缝网络结构，构建了油气从基质微纳米级孔喉到井筒运移的核心通道，是关系到非常规资源能否实现工业性开发的核心和关键。同时，随着体积化压裂改造措施在非常规储层中的规模化推广应用，学者对压裂改造后储层裂缝结构的认识也由之前的双翼对称张性裂缝扩展至张性裂缝和剪切滑移裂缝的组合［5］。

现阶段，关于裂缝结构中流体渗流的研究主要集中于张性裂缝结构［6-10］;相较于张性裂缝，剪切滑移裂缝面间是非匹配的。两者在裂缝结构上的差异决定了目前在张性裂缝研究中，相对成熟的表征、等效处理及渗透率计算等方面的理论并不能应用于剪切滑移裂缝结构中［11-12］。目前，关于剪切滑移裂缝结构的研究尚不成熟，关于剪切滑移裂缝中流体渗流规律的研究尚处于探索阶段。可见的报道主要以实验研究为主［13-14］：采用在张性裂缝两侧不同方向上依次垫加一定数量的薄铜片，或在张性裂缝两侧不同方向上依次切割裂缝结构的方式制作剪切滑移裂缝模型;然后采用实验方法，测试剪切滑移作用对流体在裂缝中渗流的影响。但是，以上两种制作剪切滑移裂缝物理模型的方法都存在着，物理模型尺寸在研究过程中非恒定的缺陷，无法确保实验结果的可信度。

明确剪切滑移作用对流体在裂缝中渗流能力的影响，对掌握流体在储层改造体积网络中的渗流规律具有重要意义。因此，本研究首先以实例，分析物理实验方法的缺陷，然后引入数值模拟方法，研究剪切滑移裂缝中流体的渗流特征，以期为研究流体在储层改造体积网络中的渗流规律提供支撑。

1 流体在剪切滑移裂缝中运移的分析测试研究

以在张性裂缝两侧不同方向上依次垫加薄铜片的剪切滑移物理模型为例，进行剪切滑移物理试验，并结合实际的具体数据分析该实验方法所造成的误差。此外，实验过程中，在外界压力环境下，实验样品的重复性测试必然会对裂缝面产生磨损，导致实验结果失真。

1.1 剪切滑移裂缝中流体渗流能力评价实验的误差分析

裂缝结构剪切滑移实验的具体操作采用Guo等人推荐的方法［13］： 在张性裂缝两侧的不同位置处， 逐渐垫加薄铜片以模拟剪切滑移裂缝结构， 考察流体在剪切滑移裂缝中的渗流能力。 实验中共采用5组不同的页岩裂缝结构， 采用的薄铜片平均厚度为0.05 mm， 考察的剪切滑移范围设定在0～0.5 mm。 具体的实验结果如图1所示。 从图1可以看出，流体在裂缝中的渗流能力随剪切滑移距离的增加总体呈增大趋势，但在部分剪切滑移裂缝中，流体的渗流能力具有较大幅度的波动。裂缝开度和流体渗流通道形态，随剪切滑移距离的增加而发生变化，由于裂缝面形态分布的复杂性，剪切滑移距离与裂缝开度、流体渗流通道形态等因素并非简单的对应关系，进而导致流体渗流能力并非与剪切滑移距离呈正相关关系。

1.2 实验误差分析

鉴于实际三维裂缝结构的复杂性，以随机选取的张性裂缝剖面线为例，阐述该实验方法的缺陷。①研究目标尺寸方面：在模拟剪切滑移裂缝时，随剪切滑移距离的增加，所需垫加的铜片数量必然增加，进而造成所模拟的裂缝结构尺寸呈逐渐增加的趋势。②裂缝结构粗糙度方面：所垫铜片数随剪切滑移的距离增加而增加，由于铜片的粗糙度为0，势必会造成研究目标的平均粗糙度随剪切滑移距离的增加而呈下降趋势。③所垫铜片位置的裂缝开度明显要比其他位置处的开度大，因此，随剪切滑移距离的增加，裂缝平均开度必然呈增加趋势。目前的实验方法中存在以上3方面的缺陷，必然会导致实验结果不可信。陈勉等［14］采用依次切割张性裂缝结构的方式制作剪切滑移裂缝模型，消除了垫铜片方法在裂缝粗糙度和开度方面的缺陷，但同样存在着研究目标尺寸在研究过程中非恒定的缺陷，实验结果可信度偏低。

以随机选取的图2所示剖面线结构为例，进行实验物理模型相關参数的误差分析。将二维结构的初始平均开度设为0.2 mm（见图3，4），随剪切滑移距离的增加，实验物理模型的实际平均开度和误差均呈线性增长趋势，且当滑移距离为0.6mm时，平均开度的误差达到约13％。

受所垫薄铜片处粗糙度的影响，剖面线粗糙度随剪切滑移距离的增加而呈线性下降趋势，进而导致物理模型的粗糙度偏差呈增长趋势，且在剪切滑移距离达到0.6mm时，物理模型粗糙度误差约为9.3％。

以上采用随机选取的二维剖面线结构，对剪切滑移物理模型本身存在的缺陷进行了分析，同时验证了Kassis，Guo等人在研究方法上的缺陷。为避免物理实验方法上的缺陷，本研究在固定物理模型尺寸的基础上，采用Lattice Boltzmann方法研究剪切滑移裂缝中流体的渗流特征。

2 剪切滑移裂缝中流体渗流的Lattice Boltzmann模拟

2.1 Lattice Boltzmann模拟方法

Lattice Botlzmann方法将流体的宏观运动拆分为介观尺度下格子的迁移和碰撞，同时格子密度和速度的宏观统计结果符合流体的宏观运动特征，以保证宏观和介观尺度上流体运动的一致性［15］。在流体运动的模型选择上，具体采用BGK－D3Q19模型进行相关的流体运移模拟，该模型的演化方程、平衡态分布函数及粒子

式中：k为裂缝渗透率，μm2;k′为格子尺度渗透率;b为裂缝开度，μm;r为格子分辨率。

2.2 模拟条件

模拟中采用的流体介质为水，温度设为293.15 K，流体的运动黏度为1.007×10-6m2／s，密度为998.203 kg／m3;格子单位下，通过调整松弛时间来确定运动黏度，模拟中运动黏度取1／30，格子单位下流体密度取0.22，格子声速1／3，由雷诺数计算公式计算可得格子速度为1／30。

流动模拟方面，设置入口流速和出口压力边界条件，出口压力设为大气压。不考虑流体压缩性的影响。

模拟网格采用笛卡尔正交网格方式。为确保模拟精度，取裂缝开度方向上的分辨率为10。纵向上设为光滑边界条件，裂缝面上采用标准反弹边界条件。模拟结果显示，各模拟条件下，渗流场不同位置处，流体密度和温度均保持恒定。

2.3 剪切滑移裂缝结构拆分及Lattice Botlzmann模拟分析

2.3.1 基本组成单元

1）基本组成单元的划分。将取自Barnett页岩的岩心采用巴西实验劈裂成缝，采用三维轮廓仪获取裂缝面分布数据并重构。基于三维裂缝面高度分布的复杂性，在所重构的裂缝面上，随机沿x方向11～15 mm处，在纵向（y方向）上选取4条剖面线，4条剖面线的具体高度分布如图5所示。以随机选取的4条剖面线为例，进行基本组成单元的划分。

分别以0.1，0.2，0.4 mm为测量精度选取数据，绘制并观察不同测量精度下的剖面线形态，具体如图6A所示。从图6A可以看出：剖面线形态随测量精度的不同而有较大差异;同一条剖面线，当测量精度较高时，可分解为不同V型结构的组合;剖面线形态随测量精度降低而逐渐变的平滑，可分解为不同曲率弧线结构的组合。考察测量范围对剖面线形态的影响，结果如图6B，C，D所示：图6B中，可将剖面线分解为不同曲率弧线的组合;图6C为将图6B中的剖面线横向恒定纵向拉伸，剖面线纵向上的高度分布变得相对平缓，总体上可视为平板结构的组合，局部视为平板结构和曲率弧线的组合；图6D为将图6B中的剖面线纵向保持恒定横向压缩，则剖面线纵向高度分布变化相对剧烈，此时总体上将其视为V型结构的组合，局部等效为V型结构和平板结构的组合。综合以上分析，可将随机二维剖面线拆分为V型结构、曲率弧线结构和平板结构等基本单元体。

曲率弧线结构可采用傅里叶级数表征，而傅里叶级数则是由不同振幅和角速度的正余弦曲线构成，而余弦曲线本质上是正弦曲线的横向平移。

通常在处理裂缝结构时，会将其视为平板模型或平板模型的组合，考虑到平板模型的渗流规律过于简单，因而考虑采用平板模型的组合即凹槽结构作为考察的基本组成单元。结合以上对粗糙裂缝随机二维剖面线结构的分析，可将V型结构、正弦结构和凹槽结构等3种结构作为其基本组成单元。从本质上讲，V型结构和凹槽结构均是正弦结构的特殊形式，但从研究的严谨性角度考虑，本研究采用以上3种结构作为其基本组成单元。

2）流体在剪切滑移裂缝基本组成单元中流动的模拟分析。

V型结构：

模拟中采用的V型结构物理模型由总长度为4 mm的两端平板模型和中间视长度为1.8 mm的V型结构组成;为避免滑移过程中两裂缝面产生接触，将裂缝开度恒定为0.5 mm;模拟过程中， 恒定物理模型整体长度及结构下部不变， 以0.2 mm为滑移间隔， 将上部结构逐渐向右平移。 具体模拟结果如图7所示。 从图7中可以看出， 裂缝结构的渗透率随剪切滑移距离的增加而总体上呈先下降后趋于稳定的趋势。

实例中， 当剪切滑移距离大于1 mm后， V型结构的渗透率保持恒定。 剪切滑移作用造成沿渗流方向上裂缝开度分布的非均匀性， 同时裂缝结构的渗透率也呈现数量级的减小; 当剪切滑移距离为0时， 沿渗流方向各渗流截面上的平均速度基本上成均匀态分布在0～1.9 m／s; 流体渗流速度分布范围随剪切滑移距离的增加而呈增加趋势， 当剪切滑移距离为0.8 mm时，

渗流速度分布在0～5.6 m／s，分布范围最广。裂缝开度随剪切滑移距离的增加而呈现出明显的差异性，结构差异造成沿流体渗流方向上渗流截面的变化，渗流截面的突然变化造成渗流速度的急剧变化，是造成能量损失的根本原因，最终体现在流体在其中渗流能力的降低。

正弦结构：正弦结构物理模型由两端平板结构和中间正弦结构组成，其中正弦结构视长度为1 mm，平板结构总长度为4 mm，物理模型初始开度恒定为0.25 mm，以避免剪切滑移过程中上下面产生接触；固定物理模型的下部结构，以0.2 mm为间隔将模型上部结构沿渗流方面逐渐向右平移。具体模拟结果如图8所示。从图8可以看出，裂缝结构渗透率随剪切滑移距离的增加呈迅速下降趋势，当剪切滑移距离大于0.6 mm时，正弦结构渗透率趋于稳定;剪切滑移作用导致沿渗流方向上截面积较小的区域产生局部高速区域，截面积较大区域产生局部渗流低速区域，渗流截面积的局部急剧变化使能量损失增加。与V型结构相似，剪切滑移作用同样使正弦结构渗透率产生数量级的降低。

凹槽结构：其滑移距离与裂缝渗透率的关系曲线如图9所示。从图9可以看出，渗透率随滑移距离的增加呈逐渐下降趋势，并逐渐趋于稳定;滑移距离超过1 mm后，渗透率基本趋于稳定。与V型结构和正弦结构滑移产生的现象类似，凹槽结构同样产生了局部渗流速度的明显变化区域。

根据对V型结构、正弦结构和凹槽结构的研究可知，剪切滑移作用使基本组成单元的渗透率产生数量级减小;当滑移距离达到一定值后，裂缝渗透率基本保持恒定;根据渗流单元体滑移距离与渗透率的关系可知，当渗透率达到极低时，基本上都是裂缝滑移结构中的裂縫开度达最小值时。换言之，其他条件一定时，裂缝最小开度是制约剪切滑移结构渗流能力的关键因素。

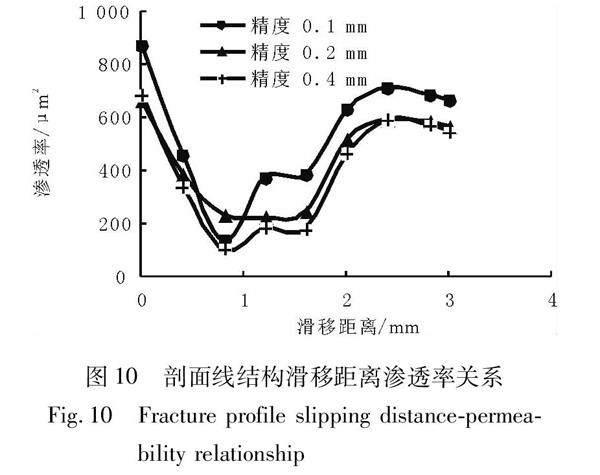
2.3.2 二维剖面线结构 实际裂缝具有大尺度匹配性、小尺度非匹配性的特征［18］，基于此，以图6A中分辨率为0.1 mm的剖面线为下侧结构，考察上侧分辨率分别为0.2，0.4 mm两种情况下剪切滑移作用对渗透率的影响，初始开度设为0.1 mm。

将截取的二维剖面线沿纵向延伸形成三维结构，在剖面线结构延伸所形成的裂缝结构右侧衔接平板结构并保持下部固定，沿渗流方向滑移上部结构，并将上部结构设定不同测量精度，考察非匹配情况下剪切滑移作用的影响。

非匹配情况下剪切滑移作用对裂缝渗流能力影响的模拟结果如图10所示。从图10可以看出，3种精度情况下，流体的渗流能力随剪切滑移距离的增加均呈先下降后上升趋势;上端面精度为0.1，0.2，0.4 mm情况下，剪切滑移结构的平均渗透率分别为545.35，444.02，414.98 μm 流体的渗流能力总体上随非匹配程度的增加呈略微下降趋势。

2.3.3 三维裂缝结构

在三维裂缝面上随机选取视面积为3 mm×1.5 mm的长方形区域，沿长度方向以视长度0.2 mm为间隔，依次截取6个视面积为3 mm×1.5 mm的区域。固定起点为0的裂缝面作为裂缝下端面，依次以截取的6个裂缝面作为裂缝上端面，研究三维裂缝结构中剪切滑移作用的影响。为避免接触面积产生影响，在设定裂缝开度时确保裂缝上下面不接触。

图11为考察三维裂缝结构剪切滑移距离与渗透率的关系曲线，考察的剪切滑移距离范围为0～1 mm。从图11中可以看出，三维裂缝结构的渗透率在剪切滑移距离为0时最大;三维裂缝结构渗透率随裂缝上端面滑移距离的增加总体呈下降趋势，但下降幅度显然要比基本组成单元和二维剖面线结构要低。

考察剪切滑移距离分别为0，1.0 mm时的流体渗流路径：当剪切滑移距离为0时，沿渗流方向上的流线基本呈规则化分布;剪切滑移距离为1.0 mm时，由于结构上的非匹配性，遵循阻力最小的原则，流体的渗流轨迹呈现三维迂曲性，流线分布较为杂乱，极大地增加了渗流阻力。

采用固定研究目标尺寸的思路，暂不考虑接触面积的影响，发现剪切滑移作用会导致裂缝渗透率的降低。剪切滑移作用造成裂缝结构的非匹配特征，使裂缝开度的分布具有随机性。流体渗流受限于裂缝形态，造成流体渗流的三维迂曲性，增加了渗流阻力。

3 接触面积的影响

将劈裂形成的裂缝以固定间隔滑移后发现，裂缝面接触面积的分布具有随机性;裂缝面的非匹配性随剪切滑移距离的增加呈增加趋势。在上覆压力作用下，非匹配性区域对裂缝产生自支撑作用，提供流体渗流的通道。关于裂缝面非匹配性的影响，前面已经系统讨论过;而关于接触面积的影响，由于裂缝中流体渗流的复杂性，在油气田开发中一直没有相关方面的研究报道;在涉及裂缝中流体渗流的其他专业领域，Walsh，Zimmerman和Kirkpatrick等均提出了修正接触面积影响的方法［19-21］，其基本思想均是采用规则的障碍物将接触面积对流体渗流的阻碍作用等效化。总之，裂缝面剪切滑移所造成的非匹配性及接触面积均对裂缝结构的渗流能力有负面作用，但裂缝面间的非匹配性可以对裂缝结构起到自支撑作用。

4 结 论

1）以裂缝面随机二维剖面线为例，分析目前常用考察剪切滑移作用实验的缺陷：裂缝平均开度随滑移距离的增加呈线性增长趋势;随滑移距离增加，粗糙度呈线性下降趋势，误差呈线性增长趋势;当滑移距离为0.6 mm时，裂缝开度偏差达13％，粗糙度误差达9.3％。

2）裂缝剖面线可拆分为V型结构、正弦结构及凹槽结构3种基本单元体。随剪切滑移距离的增加，基本单元体的渗透率产生数量级的減小，呈迅速下降趋势并最终趋于稳定。其他条件固定时，裂缝最小开度是制约剪切滑移裂缝结构渗流能力的关键因素。

3）二维剖面线结构，渗透率随剪切滑移距离的增加呈先下降后升高趋势，但总体呈下降趋势;随非匹配程度的增加，二维剖面线结构渗透率呈略微下降趋势。

4）三维裂缝渗透率随剪切滑移距离的增加呈下降趋势，但下降幅度要比基本组成单元和二维剖面线结构要低。

5）考虑接触面积影响时，剪切滑移作用造成的裂缝面间接触面积的分布具有随机性。剪切滑移作用造成的裂缝面间非匹配性可以为裂缝结构提供自支撑作用，从而提供流体渗流的通道;但非匹配性及接触面积均对裂缝结构的渗流能力有负面作用。

参考文献：

［1］胥云，雷群，陈铭，等.体积改造技术理论研究进展与发展方向［J］.石油勘探与开发，2018，45（5）：874－887.

XU Y，LEI Q，CHEN M，et.al.Progress and development of volume stimulation techniques［J］.Petroleum Exploration & Development， 2018，45（5）：874－887.

［2］曾保全，程林松，李春兰，等. 特低渗透油藏压裂水平井开发效果评价［J］.石油学报，2010，31（5）：791－796.

ZENG B Q， CHENG L S， LI C L， et.al. Development evaluation of fractured horizontal wells in ultra－lwo permeability reservoirs［J］.Acta Petrolei Sinica，2010， 31（5）：791－796.

［3］郭建春，苟波，任山，等. 川西页岩-砂岩交互水平井压裂参数优化设计［J］.石油学报，2014，35（3）：511－518.

GUO J C， GOU B， REN S， et.al. Fracturing parameters optimization design for horizontal well with shale and sandstone interbeds in western Sichuan［J］.Acta Petrolei Sinica， 2014，35（3）：511－518.

［4］翁定为， 雷群，胥云，等. 缝网压裂技术及其现场应用［J］.石油学报，2011，32（2）：280－284.

WENG D W， LEI Q， XU Y， et.al. Network fracturing techniques and its application in the field［J］.Acta Petrolei Sinica， 2011，32（2）：280－284.

［5］钟建华， 刘圣鑫， 马寅生， 等.页岩宏观破裂模式与微观破裂机理［J］.石油勘探与开发，2015，42（2）：242－250.

ZHONG J H， LIU S X， MA Y S， et.al. Macro－fracture mode and micro－fracture mechanism of shale［J］.Petroleum Exploration & Development， 2015，42（2）：242－250.

［6］肖维民， 夏才初， 王伟， 等. 考虑曲折效应的粗糙节理渗流计算新公式研究［J］.岩石力学与工程学报，2011， 30（12）：2416－2425.

XIAO W M， XIA C C， WANG W， et.al. Study of a new equation for fluid flow through a single rough joint considering tortuosity effect［J］.Chinese Journal of Rock Mechanics and Engineering，2011，30（12）： 2416－2425.

［7］鞠杨，张钦刚，杨永明，等.岩体粗糙单裂隙流体渗流机制的实验研究［J］.中国科学（技术科学），2013，43（10）：1144－1154.

JU Y， ZHANG Q G， YANG Y M， et.al. An experimental investigation on the mechanism of fluid flow through single fracture of rock［J］.Science China （Technology Science），2013，43（10）：1144－1154.

［8］樊火，郑宏. 基于MRT－LBM的分形裂隙网络渗流数值模拟［J］.中国科学（科学技术）：2013，43（12）：1338－1345.

FAN H， ZHENG H. MRT－LBM－based numerical simulation of seepage flow through fractal fracture networks［J］.Science China（Science Technology）， 2013，43（12）：1338－1345.

［9］ZHANG Z Y， NEMCIK J， QIAO Q Q， et.al.A model for water flow through rock fractures based on friction factor［J］.Rock Mechanics and Rock Engineering，2015，48（2）：559－571.

［10］ XIAO W M，XIA C C，WANG W，et.al.Combined effect of tortuosity and surface roughness on estimation of flow rate through a single rough joint［J］.Journal of Geophysics and Engineering，2013，10（4）：45015－45023.

［11］ 曲冠政.粗糙裂縫结构的描述及其渗流特征研究［D］.青岛：中国石油大学（华东），2016.

［12］ 曲冠政， 曲占庆， Hazlett R D， 等. 页岩拉张型微裂缝几何特征描述及渗透率计算［J］.石油勘探与开发，2016，43（1）：115－120.

QU G Z， QU Z Q， HAZLETT R D，et.al. Geometrical description and permeability calculation about shale tensile micro－fractures［J］.Petroleum Exploration and Development，2016，43（1）：115－120.

［13］ GUO T K， ZHANG S C， GAO J， et.al. Experimental study of fracture permeability for stimulated reservoir volume（SRV） in shale formation［J］.Transport in Porous Media， 2013， 98（3）： 525－542.

［14］ 赵海峰， 陈勉， 金衍，等. 页岩气藏网状裂缝系统的岩石断裂动力学［J］.石油勘探与开发， 2012， 39（4）： 465－470.

ZHAO H F， CHEN M， JIN Y， et.al. Rock fracture kinetics of the fracture mesh system in shale gas reservoirs［J］.Petroleum Exploration&Development， 2012，39（4）：465－470.

［15］ 何雅玲， 王勇， 李庆， 等 .格子Boltzmann方法的理论与应用［M］.北京：科学出版社， 2009.

［16］ WANG Y W， WANG Y， AN Y R， et.al. LBM calculation of high－speed train aerodynamics［J］.Science China Technological Sciences， 2008， 38（11）：1795－1804.

［17］ DU T Z， LI X Q， ZHANG X L， et.al. Lattice Boltzmann Method used for the aircraft characteristics computation at high angle of attack［J］.Science China Technological Sciences，2010，53（8）：2068－2073.

［18］ GLOVER P W， MATSUKI K，HAYASHI K，et.al. Synthetic rough fractures in rocks［J］.Journal of Geophysical Research，1998，103（85）：9609－9620.

［19］ WALSH J B. Effect of pore pressure and confining pressure on fracture permeability［J］.International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts， 1981， 18（3）： 429－435.

［20］ ZIMMERMAN R W， CHEN D W， COOK N W. The effect of contact area on the permeability of fractures［J］.Journal of Hydrology， 1992， 139（4）： 79－92.

［21］ SCOTT K. Percolation and conduction［J］.Review of Modern Physics， 1973，45（4）：574－588.

（编 辑 雷雁林）

收稿日期：2019－09－29

基金项目：国家自然科学基金资助项目（51804255）；陕西省自然科学基金资助项目（2019JQ488，2019JQ－466）；中国石油科技创新基金资助项目（2018D－5007－0215）；陕西省教育厅科研计划资助项目（18JK0611）

作者简介：曲冠政，男，山东莱州人，博士，从事复杂油气藏储层增产改造及提高采收率研究。