视觉思维理论及其在高中数学教学中的运用

陈 兵

(江苏省启东中学 226200)

一、视觉思维的概念与特点

从狭义的角度分析，视觉思维是指在原有视觉意象的基础上，人对视觉信息有选择性的想象与构绘，以视觉意象促进思维活动的螺旋上升.从广义的角度分析，视觉思维是指阶段性的视觉思维发展，不仅包含了观察视觉对象的过程，同时还需要理解视觉意象，从视觉意象中体现出隐含的信息，进而通过交流与探究发展思维能力.

视觉思维理论主要具有以下三个特点：

1.来源丰富性.视觉是学习者获取所需信息的重要途径，而视觉思维理论在教学中的应用，可以让学习者在特定条件的刺激下积极主动地发现客观事物的特点、特征，然后成为视觉意象的组成元素，以视觉思维丰富学习者的思维元素来源，为学生的思维活动提供基础保障.

2.反应迅捷性.在课堂教学过程中，我们发现有时学生对于知识的理解与记忆非常容易，而有时学生们就会很难理解、记忆，究其原因是教师所呈现出的方式不同，学生的记忆效果也会出现很大的差异.而视觉思维理论在数学教学中的应用，更加侧重于运用一目了然的、通俗易懂的讲解、绘图或视频资料展示方法，让学生在直观的“形”的观察中快速反应，将客观事物与脑海中已经有的意象联系起来，通过二者类比分析的方式，达到快速记忆、深刻理解的效果.

3.发展的层次性.视觉思维发展的层次性一方面体现在发展过程的层次性，另一方面体现在发展水平的层次性，以层次性的视觉思维发展促进个体视觉思维的发展，有助于促进学生个体视觉思维的丰富性与完善性.

二、视觉思维理论在高中数学教学中的运用

1.视觉空间意象，培养空间思维

在高中数学教学中的知识总会涉及到数学对象在某一时刻的空间位置或多个数学对象的位置关系，这一现象在平面几何或立体几何方面尤为显著.从视觉思维理论的角度分析，教师应利用视觉空间意象，引领学生从视觉空间意象中发现数学规律、公式定义的本质，找到“数”与“形”之间的联系，树立数学空间思维.

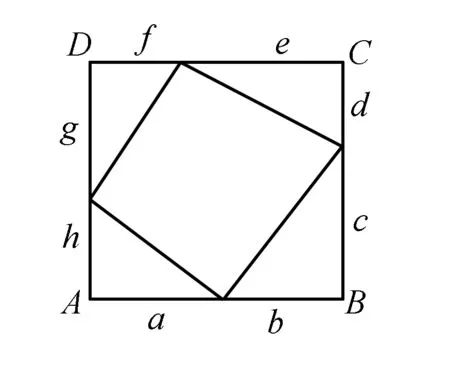
如，已知a、b、c、d、e、f、g、h均为正数，且a+b=1,c+d=1,e+f=1，g+h=1,请同学们尝试证明bc+de+fg+ha<2.在这道问题的解答中，很多学生会选择利用常规方法证明，不仅证明过程繁琐，而且失误率高.这时，教师应巧妙地引导学生从题干的已知条件中发现a+b=1,c+d=1,e+f=1，g+h=1的特点，绘制边长为1的正方形ABCD(如右图所示)，借助数形结合的方法，让原本抽象的数学文字、数学符号、数学公式变成可以直接观察的空间图形语言，以“数”与“形”的灵活转换中打造视觉空间意象，使得原本复杂的数学问题迎刃而解.

2.视觉模型意象，建立数模思想

高中生数学学习难的根源在于不善于将具体数学问题转化为合适的视觉模型意象，从数学模型中发现数学规律，利用公式解决具体数学问题.在视觉思维理论下，构建视觉模型意象，有助于学生在具体数学问题解答抓住问题的特征，明确哪些是主要因素，哪些是可以忽视的次要因素，从而借助简单、明了的理想化视觉模型意象轻松解决数学问题.高中数学教学中涉及到的视觉模型意象较多，如函数模型、方程模式、概率模型等，视觉模型意象的有效应用，对于高中生的数学学习具有很大帮助.

如，已知α+β+γ=π，求证x2+y2+z22xycosα+2yzcosβ+2zxcosγ.由于待证的是三元二次不等式，在问题解答中，教师应引导学生将x、y、z其中的一个视为未知数，将另外两个视为已知数，这样原本的三元二次不等式就变成了二次函数，构建二次函数的模型,f(x)=x2+y2+z2-(2xycosα+2yzcosβ+2zxcosγ)=x2-2(ycosα+zcosγ)x+y2+z2-2yzcosβ.通过二次函数模型证明f(x)≥0，此题故因此得证.通过视觉模型的构建，引导学生利用函数特征与性质解决不等式问题，可以优化高中生的思维品质，达到出奇制胜的效果.

3.视觉情境意象，注重发现与创造

在高中数学课程标准中明确指出数学教学应从具体实例出发，构建符合生活事实的情境展示数学知识，引领学生在数学情境中主动发现问题，经历探索与创造，从而了解数学知识的来龙去脉.视觉情境意象的构建，可以引领高中生在数学学习中入情入境，符合高中生的学习心理，让高中生在具体的、生动的视觉情境意象中激活求知欲，扩大非智力因素对高中生数学学习的积极影响.

以独立事件同时发生的概率教学为例，教师可以给学生讲述“三个臭皮匠顶一个诸葛亮”的故事，在一场比赛中，诸葛亮答对问题的概率是80%，三个臭皮匠回答正确的概率分别是50%、45%、55%，那么，在比赛中三个臭皮匠为一个队伍，诸葛亮自己一队，在问题回答中每一个人独立回答问题，队中只要有一个回答正确即可，那么请问，诸葛亮与三个臭皮匠哪一队会获胜？通过故事情境的创造，营造出愉悦的数学情境，学生在听数学故事的过程中主动思考问题，接收趣味故事中包含的数学思想，不仅增加了学生对独立事件概率的理解程度，同时也从中挖掘出了分类讨论思想，在数学故事问题情境的探索中感受到学习的乐趣.又如，在异面直线概念教学中，教师可以利用多媒体设备创设视觉情境意象，展示图片公路车道与十字交叉路口，并在十字交叉路口设置一人从东向西行走，一辆车从南向北行驶，让学生在视频资料的直观观察中发现相交直线与平行直线在生活中无处不在，但是直线相交容易产生交通事故，那么如何减少交通事故发生的机率呢？接下来继续展示立交桥的构建原理，发现平面直线与异面直线之间的差距，以视觉情境意象增加学生对数学概念理解的深刻度.

总之，视觉思维理论在高中数学教学中的应用，符合高中生的学习特点与数学学科规律，有助于促进高中生数学学习质量的提升，需要相关教师予以重视.