赋广义Orlicz范数的Orlicz函数空间的弱局部完全k-凸性

段丽芬，庄彩彩，陈洪亮

1987年，南朝勋和王建华［1］引进了弱局部完全k-凸的概念.设k≥2 为正整数，X是Banach空间，如果x0∈S(X)，{xn}⊂X,对于{ }xn的任意子列蕴含xn→w x(n→∞)，称X是弱局部完全k-凸（WLKR）的.1998年，宋力岩和张云峰［2］得到了赋Luxemburg 范数和Orlicz 范数的Orlicz 函数空间弱局部完全k-凸（WLKR）的条件.本文给出赋广义Orlicz 范数Orlicz 函数空间弱局部完全k-凸（WLKR）的判别准则.

1 定义及符号

定义1［3］若M是满足u=0 ⇔M(u)=0 的非负连续凸偶函数，则称映射M:R→[0,∞)为

设(G,Σ,μ)为一有限无原子测度空间，G上的所有可测实函数全体用L0表示.称ρM(x)=∫G M(x(t))dt，x∈L0为x关于M的模.

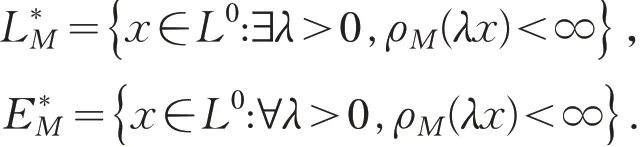
关于Orlicz范数

Luxemburg范数

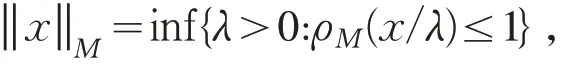
及广义Orlicz范数

均成为Banach空间［4］.在广义Orlicz范数下，简记

在Orlicz 函数空间中，“M∈Δ2”表示M(u)对较大的u满足Δ2条件，即存在K＞2 和u0≥0，使M(2u)≤KM(u)(u≥u0).

2 主要结果

定理1 设M是N-函数，则对任何1 ＜p＜∞，LM,p弱局部完全k-凸（k≥2 为正整数）的充要条件是M∈Δ2⋂∇2且M严格凸.

证明 由文献［2］中的定理1和文献［5］中的定理2，充分性直得.下证必要性.

首先证明M∈Δ2.若不然，设z(t)∈LM,pEM,p，则存在奇异泛函φ，φ(z)≠0.对x0(t)∈S(LM,p) ，取D＞0 ，使具有正测度.记，则μGn→0(n→∞).取k0满足

令

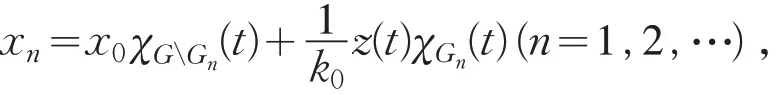
则

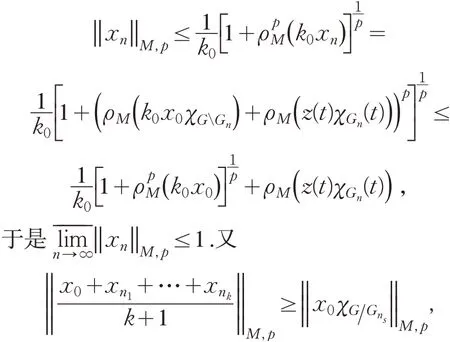
其中：ns=min{n1,n2,…,nk},有

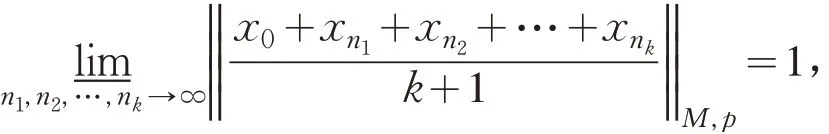
其次证明M∈∇2.不失一般性，设x0(t)∈S(LM,p)，x0(t)≥0. 因M∈Δ2，存 在y0 ∈，使得取利用积分的绝对连续性，

若M∉∇2，则存在un↑∞，满足取，则令

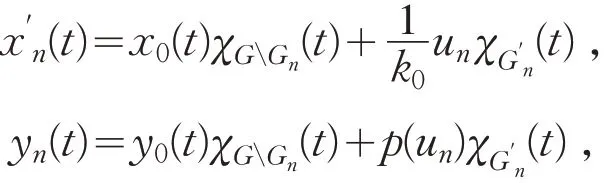
n=1,2,…，则yn(t)→y0(t)(a.e.,n→∞) ，进而因为

故

最后证明M(u)严格凸.若不然，存在u0∉SM，不妨设M(u)=Au+B,u∈[u0-ε,u0+ε].取E1⊂G，使 得0 ＜μE1＜μG且M(u0)μE1≤1,

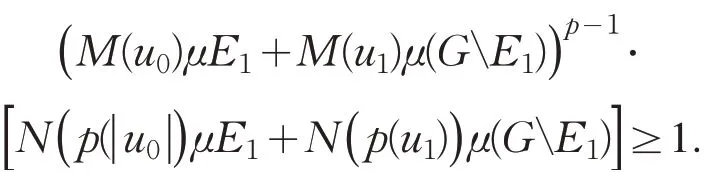
这样可选E2⊂GE1，满足

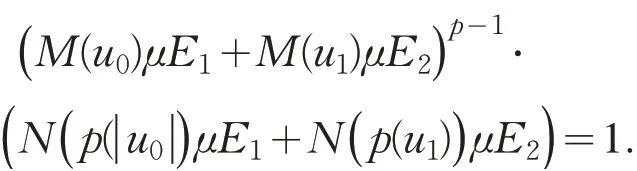
令

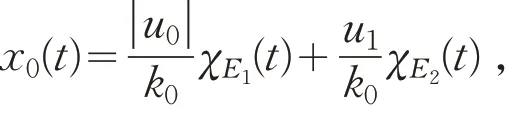
则

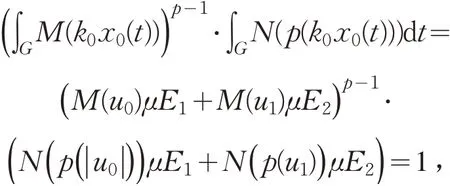
所以

将E1分成互不相交的两部分G1,G2,使得令

则

故

注意到

易得

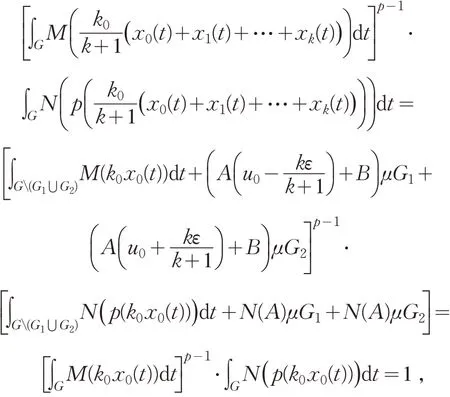
从而

取LM,p上的有界线性泛函y(t)=-χG1(t)+χG2(t),有