试卷结构的多维度研究：基于Rasch 模型的视角

李付鹏 宋吉祥 杜海燕

一、测验的多维度

在教育测验中，一般认为测验结构是单维的，目前大多数的教育考试也以单一的测验分数报告成绩。但在实践中测验往往是多维度的，多维测验一般包括两种基本类型[1，2]，试题间（between-item）多维度和试题内（within-item）多维度。试题间多维度的特征是在一个具有多个维度的测验中，每个试题仅仅隶属于某一个维度；试题内多维度则是在一个测验中存在一个或多个试题隶属于不同的维度。

测验维度分析的方法较多，包括传统的主成分分析、探索性因素分析[3，4]和验证性因素分析[5]等。在单维Rasch 模型基础上发展起来的多维随机系数多项式Logit 模型 （Multidimensional Random Coefficients Multinomial Logit Model，MRCMLM）可进行验证性因素分析。本研究运用MRCMLM 分析某高考数学试卷的能力维度，对三种可能存在的维度模型进行实验研究，最终确定一种最佳的维度模型，并在该模型框架下进行多维试题分析。

二、MRCMLM 模型

MRCMLM 模 型[6，7]是 在 单 维Rasch 模 型 基 础 上发展起来的一个通用的项目反应模型。该模型可自适应Rasch 类型的多个试题反应类型，包括常见的等级量表模型 （RSM）、 分部评分模型 （PCM）和FACET 模型等。MRCMLM 模型既可以进行单维分析，也可以进行多维可补偿分析；既可以进行二分计分分析，也可以进行多分计分分析。MRCMLM 的数学表达式如下：

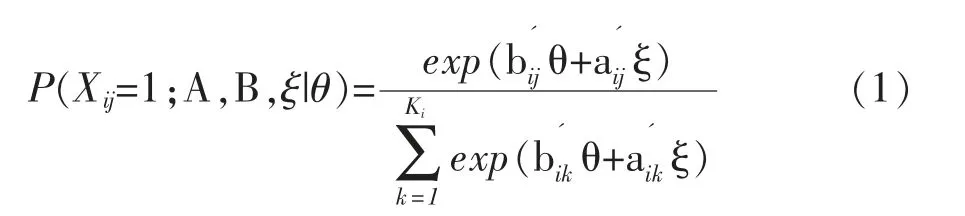
其中概率P 是能力为θ 的被试在试题i（i=1，2，…，I）类别j（=1，2，…，Ki）的反应概率，其中I 表示试题的数量，Ki表示试题i 上作答反应的类别数量。被试在试题i 的类别j 正确反应时Xij=1，否则为零，A和B 分别为设计矩阵和分数矩阵，bij是试题i 上作答反应为j 类别时对应的分数向量，aij是在试题i 上作答反应为j 类别时对应的设计向量，描述了其与试题参数向量ξ 之间的线性关系。

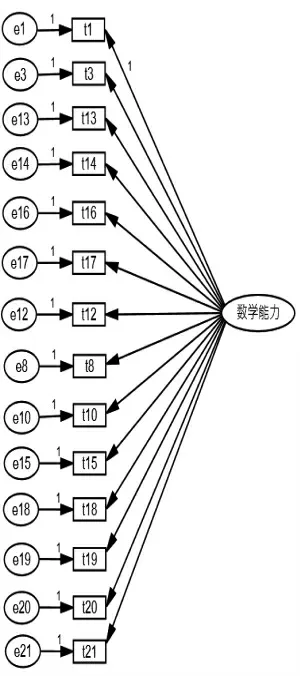
图1 模型A

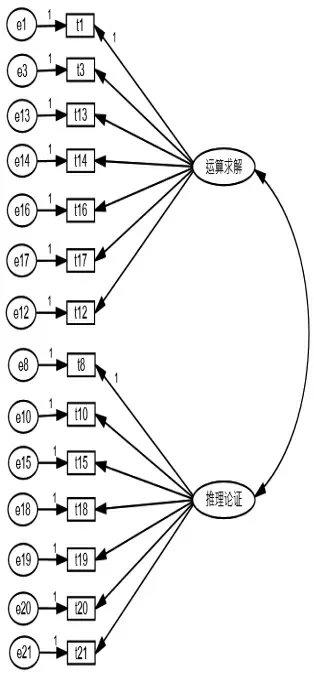
图2 模型B

三、实验设计

（一）建立模型

本研究对某省某年度普通高考数学试卷进行能力维度分析。试卷共有21 个试题，样本数量1250。从命题蓝图可知，这套试卷考查了多方面的数学能力，由于涉及抽象概括能力、数据处理能力、创新能力、应用能力、空间想象能力的试题较少，故删除了这部分试题（共7 个），保留了考查运算求解能力和推理论证能力的共14 个试题，即试卷被确定为两个主要能力维度，运算求解能力建模在第一个维度上，推理论证能力建模在第二个维度上，所有试题均按二分计分。根据专家建议，主要进行了三个模型的拟合，分别命名为模型A、模型B 和模型C，具体模型如图1、图2、图3 所示。模型A 假定所有的试题均测量一种能力，即数学方面的能力；模型B 假定第12题主要考查运算求解能力；模型C 假定第12 题考查运算求解能力和推理论证能力，其他试题的模型结构与模型B 相同。按照上述的模型分类，模型B 属于项目间的多维模型，模型C 属于既有项目间又有项目内的多维模型。

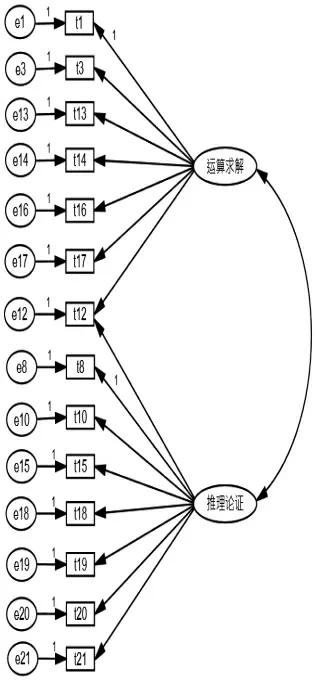
图3 模型C

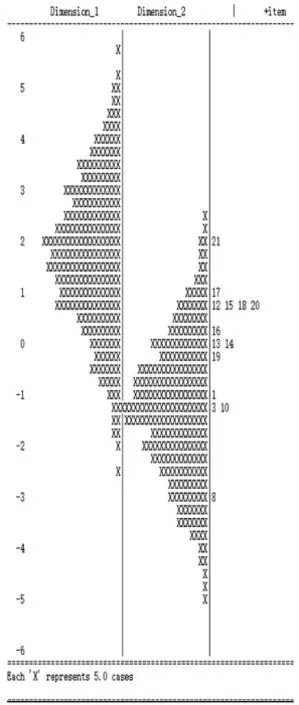
图4 模型B 多维怀特图

（二）确定模型

对于同一套试卷中的试题而言，试题与不同潜在维度之间的隶属划分，可构成不同的试卷维度模型。本研究以不同试卷维度模型与实测数据的拟合偏差大小为主要依据，同时结合方差和相关性，并以此为标准来筛选出最佳试卷维度模型[8，9]。上述两个多维模型与单维模型是层次化的关系，即模型是嵌套的，模型的拟合偏差越小，拟合度越大，就越接近真实模型。

维度拟合偏差分析。表1 给出了三个模型拟合偏差的变化，三个模型的偏差基本相当，模型A 的拟合偏差略大于模型C，模型C 的拟合偏差略大于模型B，从拟合偏差最小的角度来看，模型B 是最佳模型。Akaike 信息准则（AIC）和贝叶斯信息准则（BIC）表明，模型B 具有最小的AIC，模型A 具有最小的BIC，但从数值上来看，三个模型拟合情况基本相当。

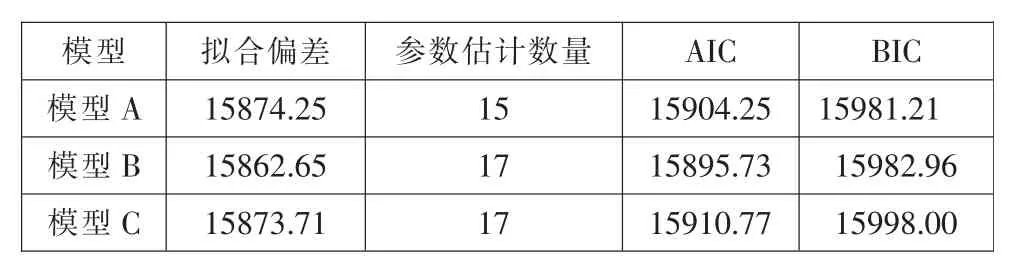
表1 模型的全局拟合度统计和信息标准

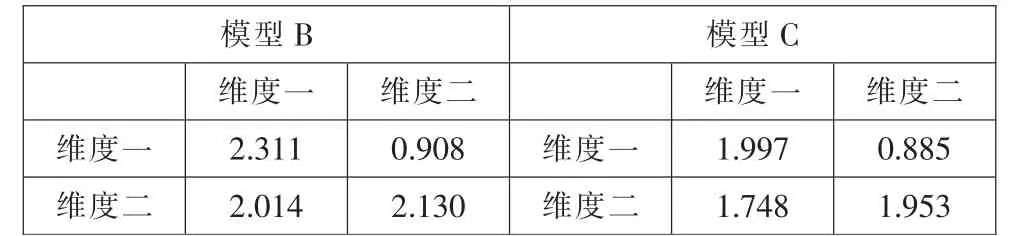
表2 模型的维度方差、协方差和相关性

维度方差和相关性分析。表2 给出了模型B 和模型C 的方差、协方差和相关性数据，其中对角元素是两个维度的方差，非对角下三角元素是两个维度的协方差，非对角线上三角表示维度之间的相关性。从两个模型维度间的相关性来看，由于MRCMLM 模型是一种补偿多维模型，它利用子测验之间的相关性来提高测量精度和可靠性，因此，应尽可能选择维度相关性较高的测量模型，由表2 可知，模型B 和模型C 各自两个维度间的相关性都比较高，模型B 维度间的相关性略大于模型C。维度间的协方差可以看作是维度间相关系数和维度方差共同作用的结果，因为对于两个给定变量X，Y，在数学上其相关性ρXY与协方差Cov（X，Y）具有如下的关系：ρXY=CovVar（X）与Var（X）表示两个变量的方差，也就是说，对于一个给定的模型，协方差和相关性的变化方向是一致的。因此，对两个模型维度间的相关性分析与协方差分析具有类似的解释。

结合上述两个方面的分析，同时考虑到模型简单化的原则，最终确定模型B 为符合试卷实际结构的最佳模型。

（三）多维分析

基于以上的分析结果，在模型B 框架下进行多维试题分析。

试题难度分布。试题难度是测验的一个重要参数，本研究通过怀特图来展示试题的难度分布.怀特图不仅给出了试题难度的分布情况，而且在同一个量尺下，也同时给出了被试反应的分布情况。B 模型下的多维怀特图如图4 所示，两个维度下的试题都具有较大的分布范围，维度一试题难度在总体上略大于维度二，但对于考生来说，两个维度的试题都略微简单。维度一第17 题和维度二第21 题分别属于两个维度中的最难试题，维度一第3 题和维度二的第8 题分别属于两个维度中的最简单试题，被试在两个维度上的分布也分别呈现对称分布。

试题特征曲面。由于模型B 和模型C 的差异主要与试卷中第12 题的维度划分有关。下面主要以第12 题的试题反应为例进行分析。在单维情况下，一般分析试题的特征曲线；在多维情况下，一般分析试题的特征曲面。图5 给出了第12 题在模型B 下考生作答概率如何随第一特质维度θ1和第二特质维度θ2变化的情况。对于仅仅具有一个维度的试题而言，学生对试题反应的概率仅仅在相关的一个潜在特质维度方向上变化，而与另一个潜在特质维度无关。图5左侧部分显示无论θ2是高还是低，都无法观测到该潜在特质对θ1的补偿情况，该试题正确回答的概率仅仅取决于θ1，相同的θ1具有相同的反应概率值。图5 右侧部分的试题等高线同样可以反映试题的差异，等高线同样清晰地表明试题仅仅与θ1有关，与θ2无关。由于模型B 中没有项目内的多维性试题存在，图5 所示的试题特征曲面和试题等高线没有体现出MRCMLM 模型的补偿性。图6 给出模型C 下第12题的试题特征反应曲面和等高线，目的是观察MRCMLM 模型的补偿性特性。图6 左侧部分显示了一种潜在特质维度可以通过其他潜在特质维度的强度来补偿，由图可知，相同的θ1由于受到θ2的补偿作用，可能具有不同的反应概率值。图6 右侧部分的等高线也显示出受到两个维度的作用。

试题信息曲面。下面仍以第12 题的试题反应为例进行试题信息曲面分析。图7 给出了两个模型下第12 题的试题信息曲面。试题信息是关于潜在特质的函数，它为深入了解试题的测量精度提供了途径。试题信息在测验构建中发挥着特别的作用。从项目反映理论的角度来看，试题提供的信息非常重要，这是试题有效性和可靠性的重要指示。图7 左侧部分显示当维度一潜在特质θ1在零附近时，第12 题提供了最大的试题信息，当维度一潜在特质θ1非常低或非常高时，试题提供的信息最低。图7 右侧部分显示当两个潜在特质θ1和θ2都在零附近时，项目信息水平最高，而当潜在特质变得非常低或非常高时，项目信息最低。

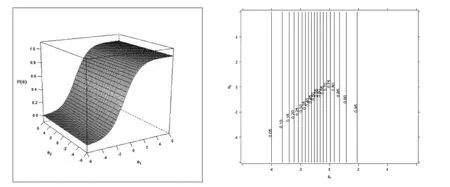
图5 模型B 试题特征曲面（左）和试题等高线（右）

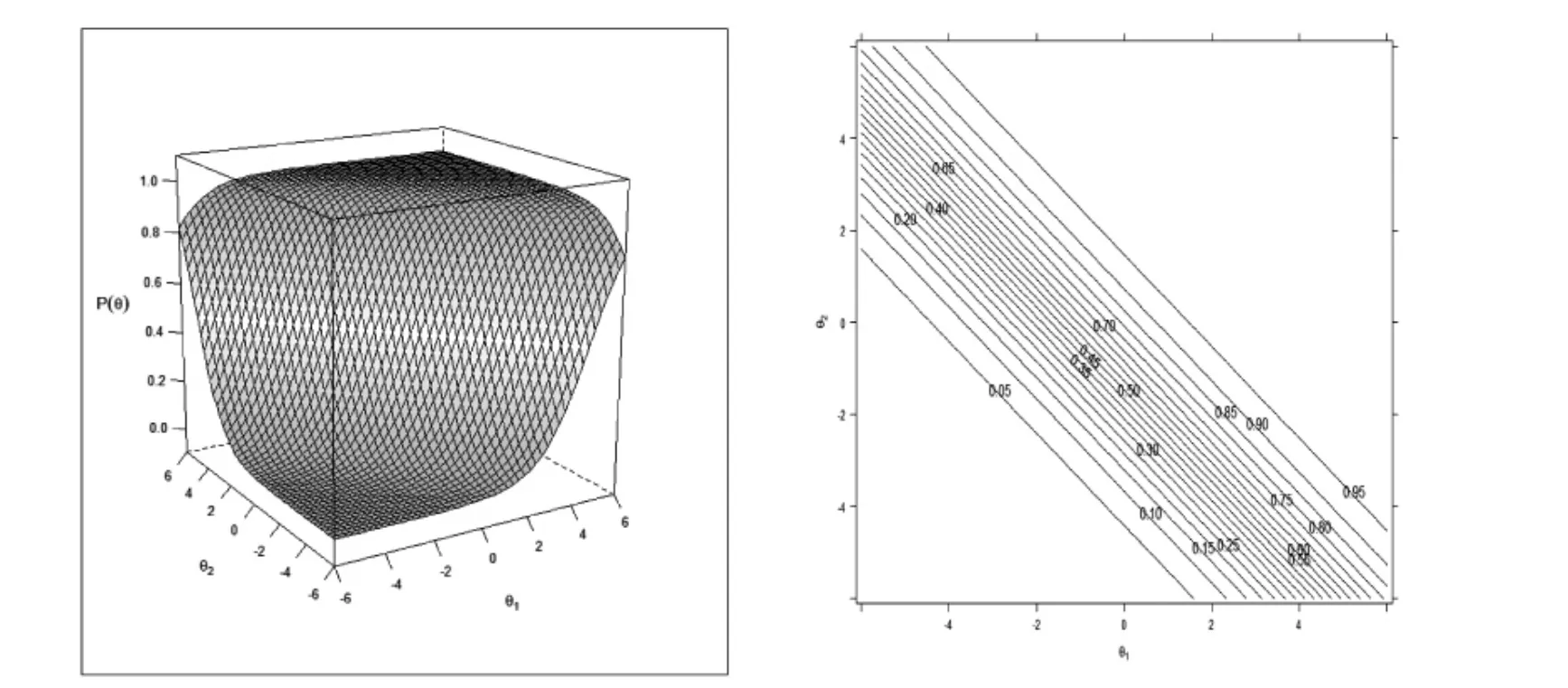
图6 模型C 试题特征曲面（左）和试题等高线（右）

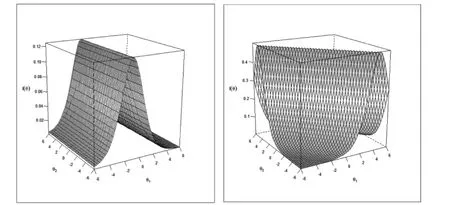
图7 模型B（左）和模型C（右）试题信息曲面

测验层面分析。测试的精度可以通过对每个试题可用的信息求和来确定，测验信息是试卷所有试题信息总的反映。通过信息函数，测验人员可以精确评估每个试题对总测验精度的贡献，从而选择与测验构建其它方面不冲突的试题。从项目反应理论的角度来看，对于一份试卷，要寻求最大的测验信息，同时获得最小的测验标准误。图8 给出了测验试题的总信息（左图）和 测验标准误的图形分布（右图）。在试题信息曲面图中，最陡坡的方向具有信息函数的最高脊。图8（左图）给出了脊线的大致位置，同时可以看出在两个维度不同坐标点的测验信息量分布，尽管两个维度上的试题数量相同，但对测验信息的总贡献不一样；图8（右图）可以看出在两个维度的不同坐标点测验标准误的分布情况，两个维度的不同特质分布坐标上的标准误在大部分区域是一致的。

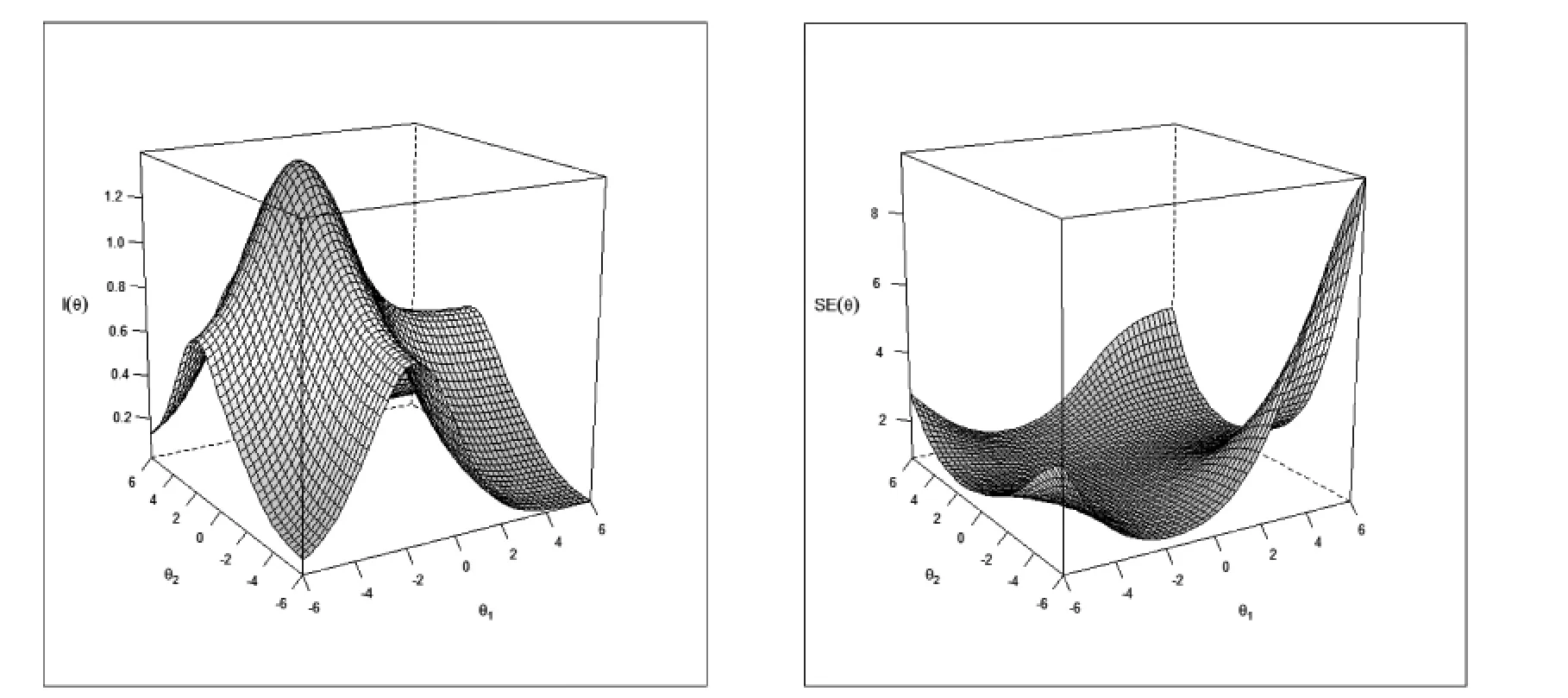
图8 测验试题信息曲面（左）和测验标准误曲面（右）

（三）结论

本文基于MRCMLM 模型，从拟合偏差、维度方差和相关性等几个方面，确定了试卷结构的多维模型，并对试卷试题进行了多维度的分析。结果表明，MRCMLM 模型是一种有效的分析试卷多维结构的工具，多维分析能够提供比单维分析更加丰富的测试信息，多维分析结果更加符合真实的试卷结构，分析也验证了MRCMLM 模型具有补偿性质。

（四）研究局限性

本次研究一个主要的局限性是所使用的考试数据没有呈现出较为明显的多维度特征，单维模型和两个多维模型的拟合偏差差异较小。在拟合偏差差异较小的情况下，以单维模型A 进行分析更加简单，但考虑到单维分析所提供的试题和试卷的信息较少，本文以模型B 为基础进行了多维度的分析。另一个局限性在于目前能够进行多维分析的三维或多维的图形化工具较少，本文利用近年来发展迅速的R语言的图形化工具实现数据的多维分析，但还不能完全满足数据分析的需要。

四、结束语

与传统因素分析方法类似，可以通过探索性因素分析或验证性因素分析的方法确定多维模型。本文采取的是验证性因素分析方法，基于近年来新发展的MRCMLM 模型，对某普通高考数学试卷可能存在的维度模型，从测验的拟合偏差、相关性角度确定最佳的维度模型，并对确定的维度模型从试题信息层面和测验信息层面作进一步分析，得到了一些有意义的结论，将该分析方法与传统的多种因素分析进行比较是本研究下一步的工作。