利用改进的超像素分割和噪声估计的图像拼接篡改定位方法
李思纤, 魏为民, 楚雪玲, 华秀茹, 栗风永
(上海电力大学 计算机科学与技术学院, 上海 200090)
在当今社会,数字图像已成为重要的信息来源.报纸新闻中的图片、法庭上的监控记录、医院里的核磁共振图像等是数字图像在各领域的应用.然而,数字图像操作的简易性使图像的真实性存疑,逼真的技术使图片难辨真假.因此,数字图像取证技术应运而生.数字图像取证技术分为主动取证技术和被动取证技术[1-4].相较于被动取证技术,主动取证技术必须事先进行信息的嵌入,具有一定的局限性[5-9].
拼接篡改是当前主流的图像篡改手段之一[10],在对拼接篡改图像进行篡改区域定位时,往往需要根据图像原有的许多特征来暴露拼接图像的局部不一致性.图像噪声就是其中非常重要的特征之一.由于不同的图像具有不同的噪声水平,局部噪声的不一致性成为检测图像拼接篡改的有力证据[10].
目前,图像噪声已经广泛应用于数字图像取证,国内外的学者在利用噪声进行图像拼接篡改的检测和定位方面开展了相关研究[11-19].然而,这些研究在噪声差异较小时都存在定位不精确和图像边缘信息保留较少的问题.基于此,本文提出一种利用改进的超像素分割和噪声估计的图像拼接篡改定位方法.
1 图像拼接篡改定位方法
1.1 算法框架
对于待检测图像,首先,使用改进的简单线性迭代聚类(SLIC)超像素分割算法进行图像分割;然后,使用基于主成分分析(PCA)方法计算局部图像块的噪声水平;最后,通过聚类算法将噪声水平相似的图像块进行聚类,并确定篡改区域.算法框架图,如图1所示.

图1 算法框架图Fig.1 Algorithm framework
1.2 基于DBSCAN的SLIC超像素分割算法
为了定位篡改区域,将测试图像分割成I个图像块,用于局部的噪声水平估计.传统的图像篡改区域定位方案是将图像分为一个个重叠块或非重叠块,对每一小块进行特征统计,然后,根据特征的差异对篡改区域进行定位.然而,这种方法即使采用较好的噪声估计算法,也难以得到比较准确的边缘信息.
文献[14,17]提出一种两阶段由粗到细的分块策略,先将图像分为64 px×64 px的图像块,进行第一次噪声估计结果分类;根据分类结果,再将图像分为32 px×32 px的图像块;最后,根据噪声估计结果进行最终的定位.这个策略可在一定程度上改善定位区域不精确的情况,但仍然无法绘制出篡改区域的边缘.因此,使用基于密度聚类(DBSCAN)的SLIC超像素分割算法对图像进行分块,相较于SLIC算法,可较好地保留图像的边缘信息.
基于DBSCAN的SLIC超像素分割算法有以下7个步骤.
步骤1设定初始种子点.设定J个种子点,这些种子点在图像内均匀地分布.
步骤2调整种子的位置.在种子的z×z邻域内,将超像素中心移动到梯度最小点.
步骤3分配标签.如果每个超像素中心2z×2z邻域内的点到超像素中心的距离小于它原来属于的超像素中心的距离,则它属于这个超像素中心.
步骤4度量距离.对搜索到的每个像素点,计算其与该种子点的颜色距离及空间距离.由于每个像素点可能会被多个种子点搜索到,因此,取颜色距离和空间距离最小值对应的种子点为该像素点的聚类中心.
步骤5迭代优化.
步骤6计算各超像素颜色中心与其邻域像素中心的距离.
步骤7使用DBSCAN算法,将超像素块进行聚类,完成最终分割.
基于DBSCAN的SLIC超像素分割算法具有以下2个优点.
1) 通过DBSCAN算法将图中关联性较大的块进行合并,使原本较小且被割裂的块合并在一起,加强图像块之间的联系,可以更精确地定位篡改区域.
2) 一般情况下,为得到详细的贴合边缘的图像块,分割的块数越多越好,从而导致分割出来的图像块较小.在噪声估算时,较小的图像块无法提供准确的噪声估计结果.该算法可以弥补以上缺点,既可分割足够多的图像块,也不用担心得到的图像块较小.
1.3 基于PCA的噪声估计算法
数字图像会引入噪声,通常噪声在整个图像上是均匀分布的.然而,图像拼接篡改往往会引入不同噪声水平的图像,根据噪声水平的不一致性即可检测出图像是否被篡改.
通过基于PCA的噪声估计算法[20]对分割后的图像块进行局部噪声水平估计,该算法是目前比较出色的噪声估计算法之一,它几乎不受图像纹理的影响,且估算准确性较高.
目前,使用最为广泛的噪声模型是加性高斯白噪声模型,即
y=x+n.
(1)
式(1)中:y为噪声图像;x为原始图像;n是具有方差为σ2的零均值高斯白噪声.
首先,假设x是尺寸为S1×S2的原始无噪声图像,其中,S1为列数,S2为行数.y=x+n是由与信号无关的加性高斯白噪声生成的图像,每个x,n,y中都包含N=(S1-M1+1)×(S2-M2+1)个大小为M1×M2的块,M1,M2皆为像素长度,图像块左上角位置取自集合{1,…,S1-M1+1}×{1,…,S2-M2+1},这些块可以被重新排列成具有M=M1×M2个元素的向量,子图像块xi,ni,yi(i=1,…,N)被分别视为随机向量X,N和Y的实现[20].由于n是与信号无关的零均值高斯白噪声,故N~NM(0,σ2I)且cov(X,N)=0,I为单位矩阵.
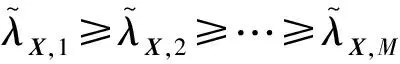
定义一类无噪声的图像,并满足以下假设:m是预定义的正整数,无噪声图像x中的信息是冗余的,因为所有的xi都位于子空间VM-m⊂RM中,其维数M-m小于M.
(2)
式(2)中:i=M-m+1,…,M;O表示存在一个数,可使该式成立.
步骤1将y分解为重叠的小块,其大小为4 px×4 px,5 px×5 px或6 px×6 px.
步骤2计算σ2ub=C0Q(p0).σ2ub为真实噪声方差的上限,真实的噪声方差不会更高,设C0为3.1,p0为0.000 5,Q为求分位数的函数[20].
步骤3通过递归丢弃方差最大的块直到满足先前的假设,根据YP={yi|s2(yi)≤Q(p),i=1,…,N}选择图像块的子集,YP为图像补丁的子集,Q(p)为p分位数.
步骤4估计当前的噪声水平.迭代步骤3和步骤4,直到收敛.
与现有的噪声水平估计方法相比,基于PCA的噪声水平估计方法在精度和速度方面都具有良好的表现,故以此为图像特征.
1.4 聚类
1.4.1 数据预处理 估算每个图像块的噪声水平后,通过对噪声数据的聚类可以得到篡改区域.然而,在实验过程中,常常有一些异常的数值干扰聚类结果.因此,需对估计得到的噪声数据进行一定的预处理操作.处理后的数据更平滑,后续聚类操作的结果更准确.文中采用对数函数转换的方式,对数据进行非线性归一化处理,即w=log(u,2).其中,w为处理后的噪声数据;u为处理前的噪声数据.
1.4.2 聚类算法 聚类的目的是将具有相似噪声水平的图像块聚集在一起.在拼接图像中,被篡改的区域往往较小,因此,认为聚类结果中数目较小的类所构成的区域是篡改区域.运用3种聚类算法对噪声估计结果进行聚类,以评估出效果最好的算法.
1)K-means算法.K-means算法将a个点划分到b个聚类中,其中,每个点都属于离它最近的均值(即聚类中心)对应的聚类,这些点可以是样本的一次观察或一个实例.该算法的缺点在于其最开始是通过随机的方法选取数据集中的c个点作为聚类中心.
2)K-means++算法.K-means++算法对K-means算法进行改进,其假设已经选取d个初始聚类中心(0 3) DBSCAN算法.DBSCAN给定空间里的一个点的集合,把附近的点分成一组,并标记出处于低密度区域的局外点.DBSCAN能在具有噪声的空间数据库中发现任意形状的簇,将密度大的相邻区域连接,有效地处理异常数据. 使用哥伦比亚大学彩色拼接图像库DVMM[21]进行测试实验.数据集共有363幅图像,其中,183幅图像是真实图像,180幅是拼接图像.图像来自不同数码相机拍摄的真实图像,图像为TIFF格式,尺寸范围为757 px×568 px至1 152 px×768 px.这些图像主要为室内场景,如办公桌、计算机、走廊等. 以图像1~4为例,对3种聚类算法进行测试.3种聚类算法定位效果的比较,如图2所示.由图2可知:K-means++算法的定位效果最好,K-means算法次之,DBSCAN算法定位效果较差. (a) 拼接篡改图(图像1) (b) K-means(图像1) (c) K-means++(图像1) (d) DBSCAN(图像1) (e) 拼接篡改图(图像2) (f) K-means(图像2) (g) K-means++(图像2) (h) DBSCAN(图像2) (i) 拼接篡改图(图像3) (j) K-means(图像3) (k) K-means++(图像3) (l) DBSCAN(图像3) (m) 拼接篡改图(图像4) (n) K-means(图像4) (o) K-means++(图像4) (p) DBSCAN(图像4)图2 3种聚类算法定位效果的比较Fig.2 Comparison of localization effects of three clustering algorithms 表1 3种聚类算法的性能指标对比Tab.1 Comparison of performance indicators of three clustering algorithms % 采用2个性能指标(真阳性率RTP和假阳性率RFP)评估这3种聚类算法,RTP=TP/(TP+FN)×100%,RFP=FP/(FP+TN)×100%.上式中:FN为假反例,被判定为负样本,但事实上是正样本;FP为假正例,被判定为正样本,但事实上是负样本;TN为真反例,被判定为负样本,事实上也是负样本;TP为真正例,被判定为正样本,事实上也是正样本. 3种聚类算法的性能指标对比,如表1所示. 以图像5~9为例,对于采用文中方法(K-means++聚类算法)与现有方法(文献[16]方法、文献[17]方法)的定位效果进行比较,如图3所示.实验所用图像均来自图像库DVMM,或使用Photoshop在Flickr.com网站上拼接得到. (a) 拼接篡改图(图像5) (b) 文献[16]方法(图像5) (c) 文献[17]方法(图像5) (d) 文中方法(图像5) (e) 拼接篡改图(图像6) (f) 文献[16]方法(图像6) (g) 文献[17]方法(图像6) (h) 文中方法(图像6) (i) 拼接篡改图(图像7) (j) 文献[16]方法(图像7) (k) 文献[17]方法(图像7) (l) 文中方法(图像7) (m) 拼接篡改图(图像8) (n) 文献[16]方法(图像8) (o) 文献[17]方法(图像8) (p) 文中方法(图像8) (q) 拼接篡改图(图像9) (r) 文献[16]方法(图像9) (s) 文献[17]方法(图像9) (t) 文中方法(图像9)图3 文中方法与现有方法定位效果的比较Fig.3 Comparison of localization effects of proposed method and existing methods 由图3可知:文献[16]方法的定位效果较差,由于图片的噪声差异较小,只能定位出很小的区域;文献[17]方法的定位效果较好,但其无法给出较为准确的边缘信息,且存在一些误定位的情况. 表2 不同方法的的性能指标对比Tab.2 Comparison of performance indicatorsof different methods % 不同方法的的性能指标对比,如表2所示.由表2可知:文中方法的定位效果表现较好. 为了进一步研究文中方法的性能,对DVMM图像库中的所有图像进行定位实验.实验得到文献[16]方法、文献[17]方法和文中方法的RTP分别为30.8%,88.6%,90.7%;文献[16]方法、文献[17]方法和文中方法的RFP分别为21.3%,15.7%,13.2%.由此可知,文中方法的检测精度高于文献[16]方法和文献[17]方法. 3种方法的接收者操作特征(ROC)曲线,如图4所示.由图4可知:文中方法的表现较好. 图4 3种方法的ROC曲线Fig.4 ROC curves of three methods 综上所述,文中方法的定位更加准确,可以减少误定位.对于一些噪声差异较小的图像,由于文中方法使用了较先进的噪声估计算法,其表现更为出色.同时,文中方法定位出的篡改区域的边缘更加平滑,可得到更为精确的拼接篡改区域. 使用3.6 GHz的CPU和8 GB RAM的计算机,通过运行时间评估文中方法的时间复杂度.文中方法、文献[16]方法、文献[17]方法每幅图像的平均运行时间分别为8.2,85.2,4.5 s. 由于文献[17]使用较为简易的图像分块算法,故其速度更快.然而,在实际操作过程中,为了获得更好的定位效果,几秒的延迟完全可以接受.因此,文中方法在实际操作中的性能较优. 提出一种图像拼接篡改区域的定位方法.利用拼接篡改区域与原始图像具有不同噪声水平的特点,对使用改进的SLIC超像素分割算法后的图像块进行局部噪声水平估计,根据噪声水平的不同,定位出拼接篡改区域.对于局部噪声水平估计中可能出现异常数据的情况,采用非线性归一化的方法对数据进行预处理,使后面的区域定位工作进行得更加顺利.在拼接篡改区域定位时,评估了较为常见的3种聚类算法(K-means,K-mean++,DBSCAN),其中,K-means++算法表现较好.在对比实验中,文中方法的性能明显优于其他方法,且定位精度更高. 综上所述,文中方法能够较好地定位拼接篡改区域,更为精确地保留拼接区域的边缘信息.今后的研究将加强算法的鲁棒性,以应对更复杂的图像篡改情况.2 结果与分析
2.1 实验数据
2.2 3种聚类算法定位效果的比较





2.3 文中方法与现有方法定位效果的比较





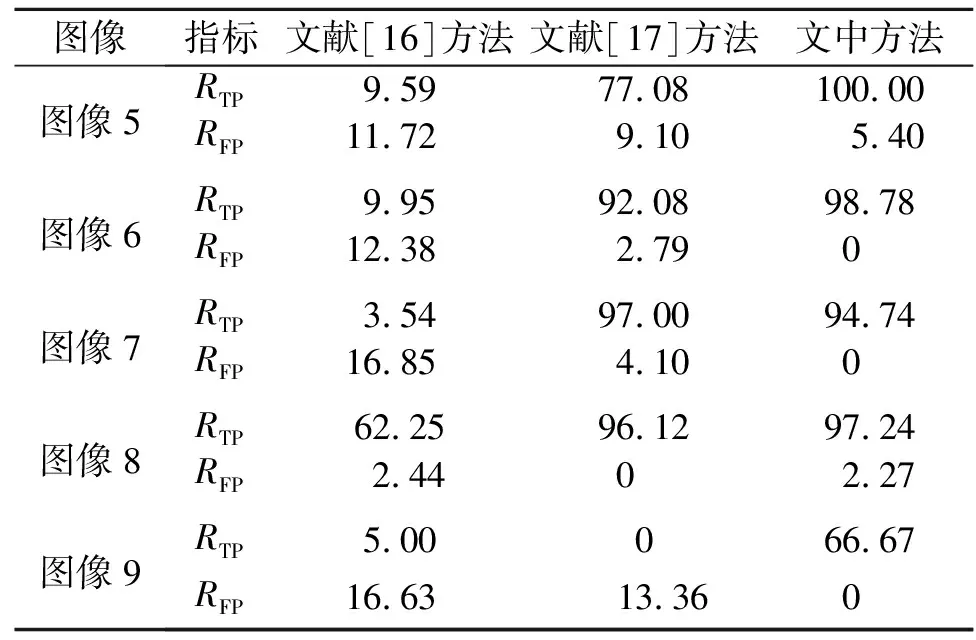

3 时间复杂度分析
4 结论

