采用复连续小波变换的桩基损伤位置识别方法
余贤英, 林城旭, 吴金福, 刘景良, 吴心坦
(1. 福建农林大学 交通与土木工程学院, 福建 福州 350002;2. 福州市第三建筑工程公司, 福建 福州 350011)
桩基作为支撑上部结构的受力构件,在各种复杂的工程地质条件下通常表现出良好的承载能力,因而被广泛地应用于高层建筑和大跨度桥梁结构中.然而,服役期间的桩基长期受到工作载荷及外部环境因素的影响,容易产生损伤并逐渐累积.因此,若不能及时发现并诊断桩身存在的损伤,将会给结构带来极大的安全隐患.对桩基进行完整性评估和损伤诊断是保障结构安全使用的必要措施之一,具有十分重要的工程应用价值.桩基的完整性评估通常通过静力或动力试验实现[1-2].静力试验由于需要大型加载设备,往往测试不方便且十分费时[3];而动力试验因设备携带便利且检测速度较快,在桩身质量评价中得到广泛的应用[4].桩基动力试验方法包括低应变和高应变试验.其中,低应变试验方法对桩身破坏较小,特别适合桩身的完整性评估,如反射波(SE)法和脉冲响应(IR)法[5-6].小波变换作为一种新型时频分析技术,已在桩身损伤检测中得到广泛的应用[7-9].Park等[10-11]利用谐波小波分析(HWAW)和反射波法对不同模式的反射信号进行数值求解.Ni等[12-13]采用连续小波变换(CWT)对尚未埋入土中的桩身进行一系列低应变试验和损伤识别研究.
由于桩身损伤引起的反射波振幅变化常常被入射波掩盖,仅根据振幅的变化并不能很好地判定桩身的损伤位置.相比之下,相位信息对损伤位置更为敏感,而复连续小波变换(CCWT)能够更好地提取相位信息,故可用于识别桩身的损伤位置.基于此,本文引入CCWT提取反射波信号的相位交叉点信息,识别桩身的具体损伤位置,并通过数值算例和桩基实例对基于复连续小波变换的桩基损伤位置识别方法进行验证.
1 基本原理
1.1 低应变反射波法

图1 一维弹性杆Fig.1 One-dimensional elastic bar
低应变反射波法又称锤击法,是一种基于一维弹性杆应力波波动理论的无损检测方法.该方法在桩顶施加激振信号,产生应力波,应力波在沿桩身传播的过程中可能遭遇不连续界面,导致该截面的阻抗发生变化,从而产生反射波.通过分析反射波信号的幅值及相位特征,可评估桩身的完整性.
假定桩为一维弹性杆(图1),其长度为L,横截面积为S,弹性模量为E,桩身质量密度为ρ,弹性波波速为c.以单元dx为对象,建立x方向的平衡方程为

(1)
式(1)中:u,t和σx分别为位移、时间和截面应力.

(2)
当桩身的横截面面积S发生变化时,相应的广义波阻抗Z也将发生变化.根据应力波理论,当应力波到达波阻抗界面时,损伤处的应力波传递公式[14]可表示为

(3)
式(3)中:vi,vr,vt分别为入射波、反射波和透射波;Z1=ρcS1为入射面的波阻抗,S1为桩身完整截面面积;Z2=ρcS2为反射面的波阻抗,S2为桩身损伤截面面积.
1.2 复连续小波变换
小波变换继承和发展短时傅里叶变换局部化的思想,克服窗口大小不随频率变化的缺点,是信号时频分析和处理的理想工具.其中,复高斯连续小波变换能够获得良好的时间和频率集中度,特别适合信号的相位分析.复高斯小波母函数的数学表达式为
ψ(t)=Cpexp(t2)·exp(-jt).
(4)
式(4)中:Cp是当|ψ(t)p|2=1时的缩放参数,ψ(t)p为ψ(t)的p阶导数.
任意信号x(t)的复高斯连续小波变换为

(5)


图2 桩长判别流程图Fig.2 Flowchart of pile length evaluation
由式(5)可得Wx(a,b),而其对应的相位角φ(t)可表示为

(6)
式(6)中:WR(a,b),WI(a,b)分别为Wx(a,b)的实部与虚部.
1.3 桩长估计
桩长判别流程图,如图2所示.在应力波传播过程中,反射波通常产生在桩的损伤截面和底部截面上.但是,与桩底反射波的能量相比,损伤截面的反射波能量很小,可以忽略不计.在对实测响应信号进行连续小波变换后,桩顶入射波和桩底反射波(并非受损截面反射波)在小波量图上形成两个高亮显示的能量集中点.
因此,可根据时频面上的亮点准确估计时间差,再根据一维波动理论计算桩长L,即

图3 损伤位置判别流程图Fig.3 Flowchart of pile damage localization

(7)
式(7)中:c为弹性波波速;Δt为应力波从桩顶传播到桩底,再反射回桩顶的时间差.
1.4 损伤定位
损伤位置判别流程图,如图3所示.当桩身材质均匀且没有损伤时,相位角映射图在时频面上表现为一组等间隔的直线;而当桩身受损时,映射图上会出现交叉点.只有当与交叉点相关的能量存在时,此处的交叉点才可判定为真正的损伤点.由此,再绘出交叉点处频率所对应的时间-相位角曲线,并验证该点的正确性[15].找出时间-相位角曲线中的相位变化点n后,计算该点与桩头之间的时间差Δtn.最后,用Δtn替换式(7)中的Δt,可得桩身损伤截面至桩顶的距离Ln,即

图4 考虑桩土相互作用的桩身有限元模型(单点损伤)Fig.4 Finite element model of pile consideringpile-soil interaction (single point damage)

(8)
2 数值算例验证
2.1 单点损伤
采用ABAQUS软件对混凝土桩身与周围土体进行三维有限元模拟,其有限元模型(单点损伤)如图4所示.设定桩长为20 m,直径为1 m,有18 m埋入土中,预定损伤位置距离桩头9 m.由于混凝土桩的长细比远大于5,可满足一维波动理论的前提条件,因此,采用基于一维波动理论的低应变反射波法进行桩身的完整性分析.
设定周围土体的直径是桩径的5倍,土体范围可视为足够大,避免应力波从远处边界传回预设的传感器.混凝土桩的弹性模量为37.5 GPa,泊松比为0.167,密度为2 400 kg·m-3.土体采用黏土,弹性模量为6.0 MPa,泊松比为0.400,密度为1 750 kg·m-3.土体的不排水强度通过库伦模型进行模拟,其中,黏聚力为25 kPa,内摩擦角为20°[16].桩土之间采用面对面接触,接触行为有切向行为和法向行为,将切向行为的摩擦系数设为0.3,法向行为设为硬接触.
在初始分析步中,首先,约束土体左右两侧的位移,将土体底部完全固结.然后,约束桩身左右两侧的位移,并保留桩身上下方向的位移.桩身损伤类型定义为颈缩,颈缩后的直径为0.95 m,即桩身截面损伤程度为10%.定义的桩身损伤沿截面法向的长度为0.5 m,损伤位置距离桩顶9 m.在静力分析步中,对桩土模型施加1个重力荷载;在动力分析步中,采用脉冲荷载作为外加激励,对桩顶圆心处(30号点)施加一个冲击荷载,大小为5 kN,持续时间0.1 ms.设定时间间隔为0.2 ms,时间总长为20 ms,通过隐式动力分析获取桩顶圆心附近处(543号点)的反射波速度响应信号,如图5所示.

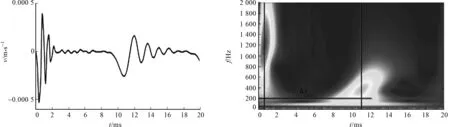
图5 反射波速度响应图(单点损伤) 图6 反射波信号的小波能量图(单点损伤) Fig.5 Velocity response of reflected waves Fig.6 Wavelet energy of reflected wave signals (single point damage) (single point damage)
其次,进行损伤定位.对反射波速度响应信号(图5)进行复高斯连续小波变换,并根据式(6)计算得到相位角.将相位角映射到时频面上,并进行灰度处理,结果如图7所示.图7中:白色表示相位角是180°(π);黑色表示相位角为-180°(-π).根据前面所确定的能量集中区域,可将频率范围限制于200~2 000 Hz,而时间范围限制于0.6~11.1 ms.因此,在A~D等4点(图7)围成的区间范围内进行交叉点的搜索,可得到交叉点(相位变化点)1~3,其对应的频率分别为810,1 174,600 Hz.3个交叉点不同频率下的时间-相位角曲线,如图8所示.
由图8可知:各交叉点对应的相位角发生了变化,且相位变化点1~3对应的时间差Δt1~Δt3分别为4.25,7.18,7.62 ms. 由式(8)可计算出相位角变化点分别在8.40,14.19和15.06 m处出现, 其中,相位角变化点1在离桩头8.40 m处,与损伤的预设位置十分吻合,且相对误差仅为6.67%.

图7 相位角映射灰度图(单点损伤) Fig.7 Grayscale images of phase angles (a) 810 Hz (single point damage)

(b) 1 174 Hz (c) 600 Hz图8 不同频率下的时间-相位角曲线(单点损伤)Fig.8 Time-phase angle curve with different frequencies (single point damage)

图9 考虑桩土相互作用的桩身有限元模型(多点损伤)Fig.9 Finite element model of pile consideringpile-soil interaction (multi point damage)
2.2 多点损伤
考虑多点损伤工况,模拟的两个损伤位置距离桩顶分别为8,15 m.采用ABAQUS软件对混凝土桩身与周围土体进行模拟,模型的属性、接触、约束、加载及桩身损伤类型的定义均与节2.1相同,建立的三维有限元模型(多点损伤),如图9所示.
通过隐式动力分析获取桩顶圆心附近处(543号点)的反射波速度响应信号,如图10所示.首先,进行桩长估计.对反射波速度响应信号进行连续小波变换,得到其小波能量图,如图11所示.从频率轴上看,小波能量图在200~600,600~2 000 Hz两个频率区间内均存在能量集中区域.因此,将主要的频率分析区间定为200~2 000 Hz.从时间轴上看,小波量图不仅在0.7 ms左右存在明显的能量集中,在11.0 ms左右也出现了能量集中.其中,0.7 ms处出现的能量集中是由入射波引起的,而11.0 ms左右出现的能量集中则是由桩底反射波引起的.因此,入射波能量最大点与反射波能量最大点之间的时间差Δt=11.0-0.7=10.3 ms,上文已经求得应力波传播速度c.将两个数值代入式(7),可估算出桩长L=20.36 m.与桩长理论值相比,估算结果的相对误差为1.8%,在可接受的工程误差范围内.

图10 反射波速度响应图(多点损伤) 图11 反射波信号的小波能量图(多点损伤) Fig.10 Velocity response of reflected waves Fig.11 Wavelet energy of reflected wave signals (multi point damage) (multi point damage)
其次,进行损伤定位.对反射波速度响应信号进行复高斯连续小波变换,计算得到相位角.将相位角映射到时频面上并进行灰度处理,结果如图12所示.根据确定的能量集中区域,可将频率范围限制于200~2 000 Hz,时间范围限制于0.7~11.0 ms.因此,在A~D等4点(图12)围成的区间范围内进行交叉点的搜索,可得到4个交叉点.其中,交叉点1,2对应的频率为600 Hz,交叉点3,4对应的频率分别为740,360 Hz.
4个相位变化点在不同频率下的时间-相位角曲线,如图13所示.由图13可知:各交叉点在时间相位角图中对应的相位角发生了变化,且相位变化点1~4所对应的时间差Δt1~Δt4分别为3.72,7.15,5.30,6.20 ms.根据式(8)可计算出相位角变化点分别在7.35,14.13,10.48,12.25 m处出现,其中,相位角变化点1,2分别在离桩头7.35,14.13 m处,与损伤的预设位置(离桩头8,15 m处)十分吻合,相对误差分别为8.13%,5.80%.

图12 相位角映射灰度图(多点损伤) Fig.12 Grayscale images of phase angles (a) 600 Hz (multi point damage)

(b) 740 Hz (c) 360 Hz图13 不同频率下的时间-相位角曲线(多点损伤)Fig.13 Time-phase angle curve with different frequencies (multi point damage)
2.3 参数分析
上文仅考虑桩身损伤位置距桩顶9 m处的单点损伤,以及桩身损伤位置距桩顶8,15 m处的多点损伤两种工况.为比较不同损伤位置下该方法的识别效果,定义13种桩基损伤工况(DC1~DC13),其损伤类型均为颈缩,颈缩截面直径均为0.95 m,激励类型均为脉冲荷载.不同损伤工况下的损伤识别结果,如表1所示.表1中:η为相对误差;k为干扰点个数.

表1 不同损伤工况下的损伤识别结果Tab.1 Damage identification results of different damage conditions
由表1可知:在DC1~DC13损伤工况下,所提方法均能成功定位桩身的损伤位置,且识别结果的相对误差为5.80%~14.33%,属于工程误差可接受范围.特别地,当桩身损伤程度为10%,激励类型均为脉冲荷载时,损伤位置越靠近桩身1/2处(DC6~DC8)时,相对误差越小;损伤位置越靠近桩顶或桩底(DC1~DC3或DC12)时,相对误差越大.此外,相位角映射灰度图中还存在其他交叉点.由于它们与理论损伤结果相差较大,暂时判定为干扰点.由表1还可知:在损伤程度和激励类型固定的情况下,损伤位置越靠近桩身1/2处时,干扰点相对较少;当损伤位置越靠近桩顶或桩底时,干扰点相对较多.
3 实例验证
3.1 测试数据
通过福建省南平市的某实际桥梁桩基的测试数据,验证基于复连续小波变换的桩身损伤识别方法的有效性.待分析桩为圆形钢筋混凝土钻孔桩,直径为2 m,长度为19.8 m;桩的长细比为9.4,满足一维波动理论的应用前提.在此之前,通过超声波透射法[17]测得损伤位置距桩顶8 m处,并以此作为理论结果.低应变试验采用冲击锤对桩顶施加瞬时冲击力,然后,通过安装在桩顶的加速度传感器(灵敏度为198 mV·g-1)和桩身完整性检测(PIT)动测仪(美国PDI公司)采集加速度响应数据.现场测试装置,如图14所示.在测试中,采样间隔设为22.2 μs,即采样频率为45 kHz,采集的加速度数据经积分处理后的反射波速度响应图(实际桩),如图15所示.

图14 现场测试装置 图15 反射波速度响应图(实际桩) Fig.14 Setup of pile test Fig.15 Velocity response of reflected waves (actual pile)
3.2 实际桩长评估

图16 反射波信号的小波能量图(实际桩)Fig.16 Wavelet energy of reflected wave signals (actual pile)
对速度信号(图15)进行复高斯连续小波变换,得到其小波能量图,如图16所示.由图16可知:时频平面上有两个能量集中点.从频率轴上看,小波能量图在20~1 600 Hz频率区间内的能量密度远大于其他频段,因此,将主要的频率分析区间定于200~1 600 Hz.从时间轴上看,小波能量图不仅在2 ms左右存在明显的能量集中,同时也在12 ms左右出现能量集中.其中,2 ms时出现的能量集中是由入射波引起的,12 ms时出现的能量集中则是由桩底反射波引起的.
由图16可知:入射波能量最大点与反射波能量最大点之间的时间差Δt=12-2=10 ms,而根据混凝土强度和弹性模量求解的波速c为3 900 m·s-1.将Δt和c代入式(7),可估算桩长L=19.5 m.与桩长理论值相比,误差仅为1.52%.
3.3 实际损伤定位
对反射波速度信号(图15)进行复高斯连续小波变换,并由式(6)计算得到相位角.将相位角映射到时频面上进行灰度处理,如图17所示.图17中:白色表示相位角为180°(π),黑色表示相位角为-180°(-π).根据节3.2中确定的频率范围(200~1 600 Hz)和时间范围(2~12 ms),在A~D等4点(图17)围成的区间内进行交叉点搜索,得到3个交叉点,其对应的频率分别为440,968,418 Hz.分别绘出3个交叉点在不同频率下的时间-相位角曲线,如图18所示.

图17 相位角映射灰度图(实际桩) Fig.17 Grayscale images of phase angles (actual pile) (a) 440 Hz

(b) 968 Hz (c) 418 Hz图18 不同频率下的时间-相位角曲线(实际桩)Fig.18 Time-phase angle curve with different frequencies (actual pile)
由图18可知:各交叉点在时间-相位角曲线中对应的相位角确实发生了变化,且相位角变化点1~3对应的时间差Δt1~Δt3分别为4.5,4.8,8.8 ms.根据式(8)计算出相位角变化点分别在8.78,9.36,17.16 m处出现.相位角变化点1在离桩头8.78 m处,与超声波透射法识别结果(离桩头8 m处)较为吻合,其相对误差为9.75%;相位角变化点2,3则可判定为干扰点,干扰点的排除需结合其他桩身损伤检测方法及工程经验综合确定.
4 结论
引入复连续小波变换对桩身进行损伤定位,并通过1个数值算例和1个实桥桩基实例验证所提方法的有效性和准确性.与传统损伤检测方法相比,复连续小波变换凸显响应信号的相位信息,可成功识别桩身微小损伤的位置.
需要注意的是,该方法在识别过程中出现较多干扰点.这些干扰点是由于复杂地质条件下的桩土相互作用,以及周边环境、外部激励等因素影响而产生的,这为精确定位桩身损伤带来一定的困难.干扰点的判定和排除需要结合其他桩身损伤检测方法(如超声波透射法等)及其他工程信息(如桩的设置过程、地质情况等)进行综合考虑.

