考虑界面层和孔隙的SiCf/SiCm复合材料热膨胀性能研究*

牛宏伟，文 敏，张 帅

(中国飞行试验研究院，西安 710089)

0 引 言

目前高温合金材料在航空发动机上的使用温度已接近极限，必须寻找替代材料[1]。学界普遍认为三维编织陶瓷基复合材料是发动机高温结构材料的关键点，最终可替代金属及其合金成为发动机热端结构的首选材料[2-3]，三维编织陶瓷基复合材料一般使用C或SiC作为连续增强纤维，纤维集束三维编织制成预制体，再通过化学气相沉积(CVI)或先驱体转化(PIP)等工艺制备而成。其中界面层与纤维束和基体间具有较低的结合强度，承载时在纤维不失效的前提下允许基体发生开裂[4]，从而在保持陶瓷良好高温性能的前提下，具备优于单一基体的强度和断裂韧性[5-6]。NASA Glenn研究中心[7-8]、日本先进材料燃气轮机研究所(RIAMG)[9]分别制造出了三维编织陶瓷基复合材料涡轮导向叶片和整体叶盘，并通过实验证明了其应用潜力。

三维编织陶瓷基复合材料的热膨胀性能受到编织参数、纤维-基体界面层、基体孔隙等诸多参数的影响，对材料的热-力耦合行为研究、热强度设计来说十分重要。与基体结合后的纤维束可等效为单向纤维增强复合材料，Schapery利用能量法推导出了单向复合材料的体积膨胀系数和线膨胀系数公式，并说明了适用范围[10]；Ishikawa分别用实验和解析手段研究了单向复合材料的热膨胀系数[11]；刘书田[12]利用均匀化方法建立了热膨胀系数与组分材料性能、体分比之间的关系，发现纤维/基体性能比值对横向热膨胀系数的影响比纵向更重要。对三维编织复合材料热膨胀性能的预测高度依赖于计算模型，梁军[13]将Eshelby和Mori-Tanaka理论与刚度平均化方法相结合, 计算了含定向基体微裂纹的三维编织复合材料热膨胀系数；庞宝军[14]将纤维束和微裂纹分别看作圆柱形和原币型夹杂，考虑微裂纹的任一取向和增强纤维束的空间取向。近年来利用有限元方法对三维编织复合材料胞元结构的描述逐渐成熟，Yang[15]将复合材料胞元看成4个方向的倾斜单向层合板的组合，利用经典层合板理论可对胞元性能进行分析；Wang[16]根据编织工艺首先提出了考虑预制体中纱线拓扑的体积胞元；Sun[17]通过数值方法研究了纱线的曲率，得到了相应的几何模型；杨振宇[18]、冯伟[19]等也分别提出了三维编织复合材料的单胞模型；夏彪利用有限元模型分别计算了纤维束和三维编织复合材料整体的热膨胀系数[20]；张芳芳[21]分析了三维四向编织复合材料刚度和热物理性能随编织角和纤维体积含量的变化规律；曾黎黎[22]对现有米字型单胞模型进行改进，用空间抛物线来模拟单胞内纤维束路径，建立了螺旋型单胞几何模型。

在实验研究方面，姚学锋[23]确定了二维和三维碳纤维/环氧树脂编织结构复合材料热膨胀系数的各向异性分布特征，并了分析编织复合材料的热膨胀机理；张青[24-25]从材料内部热应力变化及结构改变的角度定性分析了不同高温处理前后3D C/SiC复合材料热膨胀系数的变化机理；李开元[26]测量了2维、2.5维和3维纤维编织结构的C/SiC复合材料从室温到1 400 ℃范围内纵向和横向热膨胀系数，以及厚度方向的热扩散系数；廖晓玲[27]研究了不同密度及高温处理前后热解碳基三维编织碳/碳复合材料的热膨胀行为，并与PAN基碳纤维以及热解碳的热膨胀性能作了比较。殷晓光[28]通过测试表明3D Cf/SiC复合材料线热膨胀系数随温度变化的规律是由于碳纤维和SiC陶瓷基体之间线热膨胀系数的不匹配及热残余应力造成的；成玲[29]采用均匀化理论与试验相结合的方法研究了碳/环氧三维编织复合材料的热膨胀特性，表明材料在编织方向上具有典型的负膨胀特性。

界面层是三维编织复合材料制备过程中在纤维表面发展出的中间层，界面层作为复合材料的基本组元之一，其结构组成和性能对材料的热膨胀系数和热应力分布规律有显著影响，需要在预测模型中合理考虑；另外，陶瓷基体中不可避免地会存在孔隙，基体孔隙对热膨胀性能的影响规律尚不明确。因此本文提出了一种考虑界面层和基体孔隙的SiCf/SiCm复合材料热膨胀系数预测方法：分别利用纤维束单胞有限元模型和混合准则计算包括纤维-界面层-基体在内的纤维束热膨胀系数；通过工业CT技术测定基体孔隙率，在改进的复合材料单胞有限元模型中通过Monte-Carlo方法构造气孔单元，以模拟基体孔隙分布的随机性，并对“开孔”与“闭孔”赋予不同的材料参数；通过单胞有限元模型的热固耦合分析得到材料纵向和横向热膨胀系数及胞元内热应力分布规律，并分析了孔隙参数对热膨胀性能的影响。最后开展预制试样自由膨胀试验对材料纵向热膨胀系数进行测定，验证了计算结果准确性。

1 理论模型

1.1 纤维束的热膨胀系数

求解纤维束热膨胀系数的主要方法有解析公式和纤维束单胞有限元模型。解析公式较为简便，但会不可避免地忽略纤维束内部界面的相互作用。纤维束单胞有限元模型更能够映射真实结构，但是建模较为复杂，当纤维含量和编织参数发生变化时，模型也会随之改变。

本文同时采用这两种方法进行计算。根据Schapery公式[10，30]，包含界面层的单向纤维增强复合材料热膨胀系数解析公式为：

(1)

(2)

其中Ei、νi、αi、Vi分别为界面层材料的弹性模量、泊松比、热膨胀系数和在纤维束中的体积分数。界面层与纤维的体积比为[31]：

(3)

纤维束单胞有限元模型基于纤维束空间结构的周期性假设，普遍采用六面体单胞模型来代表纤维束结构[19]，模型参数由下式决定：

(4)

(5)

其中D=d+2δ。有限元模型见图1，采用SOLID45单元划分网格，在纤维、界面和基体交界处采用共节点处理。

图1 纤维束单胞模型

在两两相对面的对应节点施加周期性位移边界条件和非绝热温度边界条件，研究纵向热膨胀时胞元的变形模式见图2，对于X和Y方向对称面，保持对应节点面内位移相等，面法向位移矢量和为0，即：

(6)

(7)

上标i和j表示对称面上的对应节点。

图2 胞元纵向热膨胀变形模式

材料在受热过程中的应力张量可以表达为如下形式[20]：

δij=Cijmnεmn-CijmnλmnΔT

(8)

其中σij为应力张量，Cijmn为刚度张量，εmn为应变张量，λmn为热膨胀系数张量，ΔT为温度差。当应变张量的分量全为0时，公式(1)可表示为：

σij=-CijmnλmnΔT

(9)

刚度张量Cijmn可以根据各方向的弹性常数得到，只要在计算中可以保持胞元在求解方向不发生任何变形，即保证应变εmn为0，然后给胞元一个相对于环境温度的整体温度差值ΔT，利用有限元后处理可以得到相应的支反力σij，就可求得该方向的热膨胀系数，因此对图2中的Z方向对称面，使对应节点面内位移相等，面法向位移为0，即：

(10)

横向热膨胀系数的计算原理与纵向类似。假设几何模型和材料都属于线性范围，ΔT的选择对计算结果没有影响。

1.2 基体孔隙描述

采用孔隙率这一最重要的特征参数描述基体孔隙，孔隙率的测量方法有体积法、阿基米德法、显微图像处理法等[32]，本文采用工业CT扫描成像法对孔隙率进行测定，属于显微图像处理法的一种，可通过逐层扫描叠加建立试样段的三维模型，测量结果准确率较高。图3为试样截面的扫描图像，其中基体孔隙的灰度值明显大于材料的灰度值，对整个视场进行统计，得到材料孔隙率为9.78%。

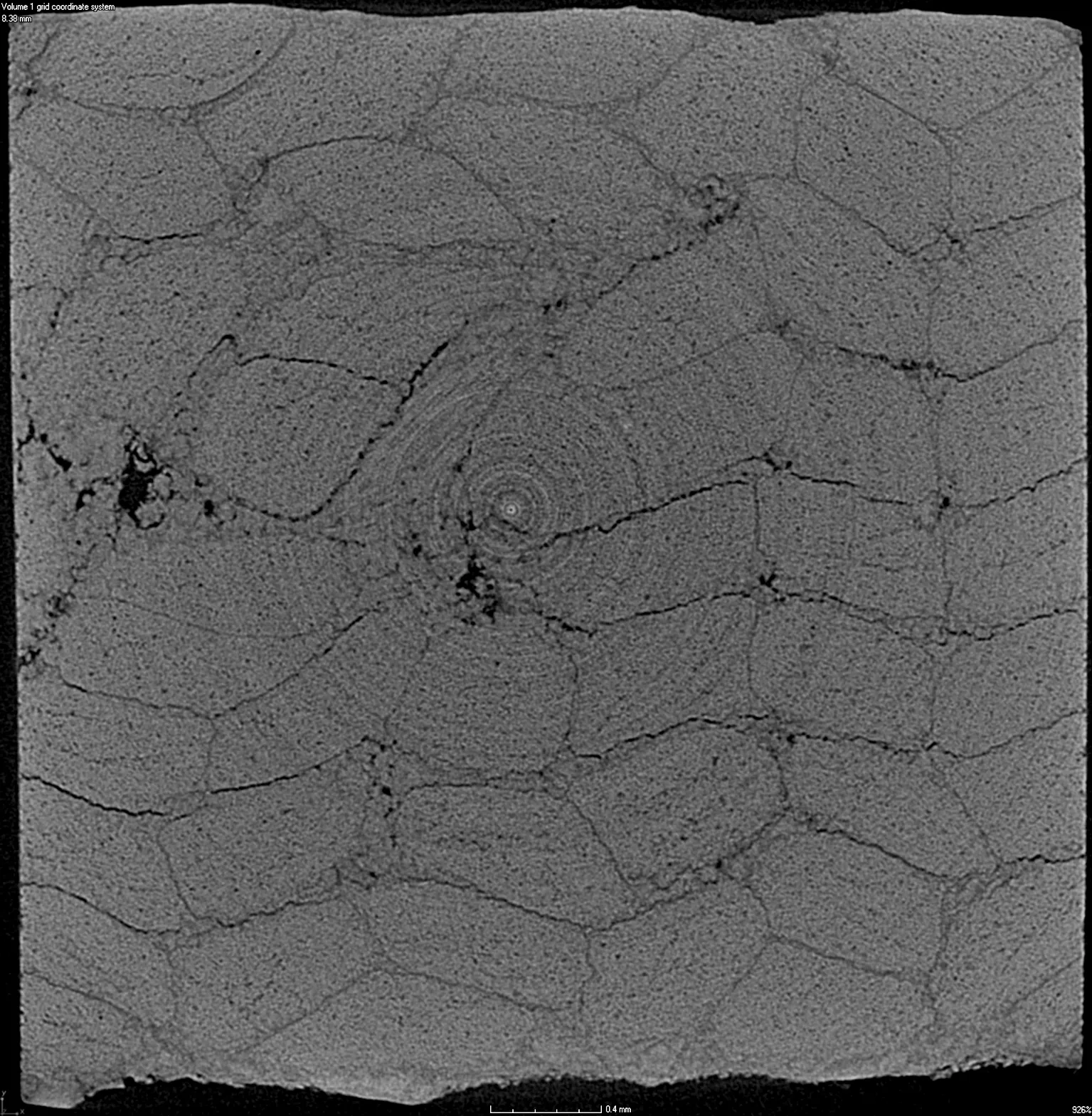
图3 试样工业CT扫描图

基体中孔隙性质的不同也会对材料宏观性能产生影响，根据孔隙与材料外部导通性的差别，可将孔隙分为“开孔”与“闭孔”，见图4，其中a为闭孔，与外界并不导通，流体无法进入，且彼此孤立；b～f为开孔，具有与材料表面相连的孔道，流体可自由流动[33]。

图4 基体中各类孔隙

由于开孔与外界连通，热膨胀率为0，而闭孔的热膨胀系数由孔隙内气体决定，以PIP工艺制备的SiC基复合材料孔隙中开孔与闭孔的体积比约为2.35[33]。根据查理定律，等压膨胀下气体的热膨胀系数为：

(11)

其中ta为当前温度，t0为初始温度。建立复合材料单胞有限元模型后，采用气孔单元法[34]在基体网格中随机投入孔隙单元，可避免在几何模型中构建孔隙所带来的网格划分问题，气孔的弹性模量取一个相对小值(10-5Pa)。

1.3 单胞有限元模型

本文采用的单胞模型是在经典的“六边形截面”交织模型[7]的基础上，考虑了打紧工艺造成的纤维束截面变形[11]，纤维束截面已经接近真实形状。根据编织体的细观结构，当给定材料的编织角γ，以及纤维体积分数V′f的情况下，单胞几何尺寸可以通过以下公式计算得到：

(12)

其中Wi和h分别为单胞的宽度和高度，Dy为纤维束等效直径。三维四向编织复合材料V′f与纤维束中的纤维体积含量Vf存在如下关系[6]：

V′f=75%×Vf

(13)

通过ANSYS APDL参数化有限元方法建立的单胞模型，见图5，各组分均采用SOLID98二阶四面体单元划分网格，图中纤维束、基体和气孔用不同颜色标出。图6为模型不同方向的视图与工业CT扫描图像的对比，可以看到模型与材料真实细观结构较为相符。

复合材料单胞模型的位移边界条件、温度载荷条件和热膨胀系数求解方法与2.1节相同。

2 计算结果与分析

2.1 热膨胀系数预测结果

该三维四向编织SiCf/SiCm复合材料采用KD-I型纤维，在表面通过化学气相沉积(CVD)制备裂解碳(PyC)界面层，并制成三维编织预制体，最后通过先驱体转化(PIP)方法制备而成，纤维体积分数为46.5%，编织角13.3°，纱线规格为1.2k，纤维直径7 μm，界面层厚度0.1 μm。纤维束中各组分结构和材料参数见表1。

图5 复合材料单胞模型

图6 单胞模型与真实结构对比

表1 纤维束中各组分基本参数

首先计算纤维束的热膨胀系数，表2列出了纤维束单胞有限元法和Schapery公式的预测结果对比，这两种方法预测纵向热膨胀系数α11较为一致，相对偏差仅为0.56%，而预测横向热膨胀系数α22差异略大，这是由于模型的基本假设不同导致的。考虑到纤维束的热膨胀系数较难测定，两种方法的优劣性还有待评估，采用Schapery公式结果作为纤维束性能基准参数。另外考虑界面层之后α11增大了1.21%，α22增大了2.96%，可见为了获取更精确的预测结果，界面层的影响不可忽略。

表2 纤维束热膨胀系数预测结果

将纤维束弹性常数和热膨胀系数输入复合材料单胞有限元模型，并在基体投入开孔和闭孔单元，保持总孔隙率和开孔/闭孔比率不变，进行20次气孔随机投入，图7为预测结果概率分布，所有结果全部落在[2.4485,2.4505]×10-6/K区间，标准差为0.000582，可见孔隙位置随机分布对材料热膨胀系数影响非常小，统计均值为：α11=2.45×10-6/K，α22=1.04×10-6/K。

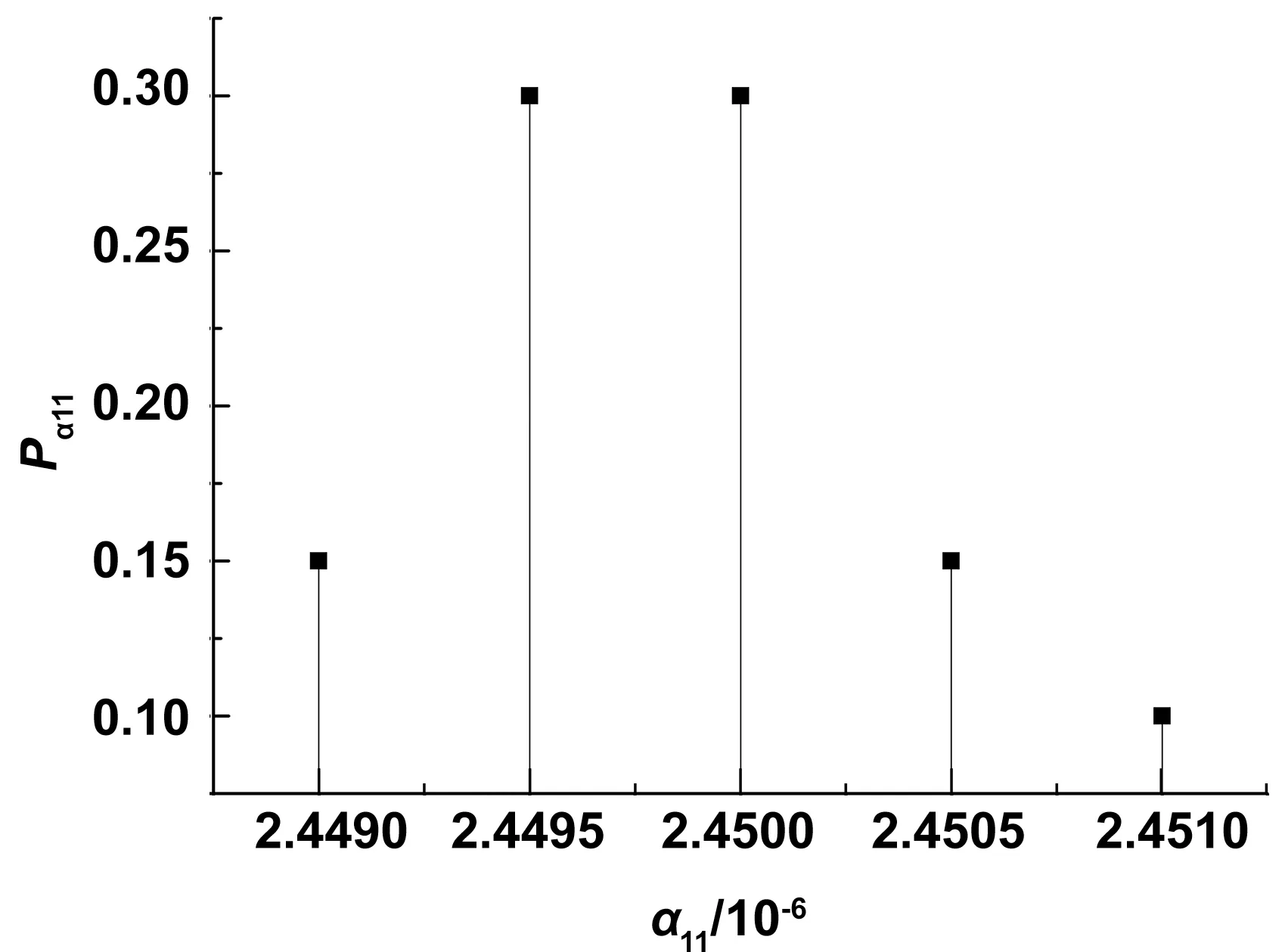
图7 复合材料α11预测结果概率分布

利用受热膨胀状态胞元的有限元预测结果，可分析复合材料内部纤维束和基体的受力状态和相互作用。图8为复合材料单胞Von Mises等效应力云图，当升温10 ℃时单胞最大应力为5.38 MPa，纤维束整体应力水平大于基体，主要有两方面原因，一是纤维束的热膨胀系数大于基体，当单胞均匀膨胀时纤维束的膨胀趋势比基体要大；二是纤维束的弹性模量大于基体，即使热应变完全相同，纤维束上所产生的热应力也要比基体大。

图8 单胞等效应力云图

2.2 孔隙参数的影响

描述孔隙的参数主要有孔隙率和开孔/闭孔比例。图9为纵向和横向热膨胀系数随孔隙率的变化关系，随着孔隙率增加，α11和α22都呈明显减小趋势，孔隙率Vpore从0增大到30%，α11减小了3.29%，α22则减小了13.06%。在孔隙中开孔和闭孔物理性质差别很大，定义为Vopen为开孔单元占总孔隙体积的百分比：

图9 热膨胀系数随孔隙率变化关系

(14)

图10为基体孔隙率Vpore=9.78%时α11随Vopen变化关系，随着Vopen增大，α11变化幅度很小，没有明显规律，推测这是由于将闭孔单元等效为热膨胀系数较大的固体单元，但由于其弹性模量赋值极小(约为基体SiC的1/10-14量级)，因此对材料整体热膨胀没有贡献，但实际上闭孔受热时内部气体的膨胀会在孔壁上产生较大压力，该方面影响需要在后续研究种持续探索。

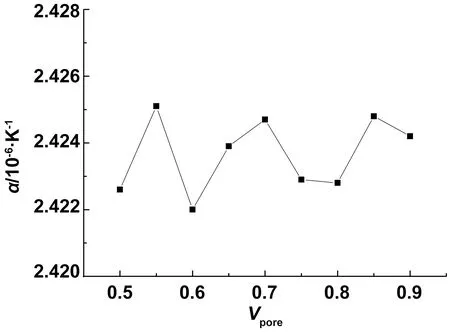
图10 α11随Vopen变化关系

3 热膨胀系数测定试验

通过SiCf/SiCm复合材料自由膨胀加温试验测定纵向热膨胀系数。试样几何尺寸按照ASTM标准设计，如图11所示，厚度为3 mm。

图11 试样几何尺寸

将试样中段放置在感应加热炉内，由上下两组加热元件进行加热，炉壁左侧装有上下两根铠装热电偶，用以监控炉内温度，加热以及温度控制均可以通过编程实现。图12为进行中的加温实验。

图12 加温实验照片

从0 ℃上升到1 100 ℃的加温时间约为2 h，在加热过程中下夹具与试样之间留有一定间隙，允许试样自由膨胀，通过高精度位移测量装置可以记录试样标距段的位移变化。记某个温度区间的温度变化量为ΔTi(i=1,2,……)，位移变化量为Δdi，标距段的长度为d=25 mm，得到该温度区间的线膨胀系数为：

(15)

取2根试样进行试验，记录其从0 ℃上升到1 100 ℃位移-温度数据，见图13，图中散点为试验数据，实线为有限元预测值。试验与理论结果基本相符，从0 ℃到1 100 ℃试样的热膨胀位移平缓增加，在1 100℃达到最大。结合图13和公式(15)，得到2根试样在各个温度的热膨胀系数，按照文献中的通用记法，线膨胀系数按表3的形式给出[19,35]。从室温到1 100 ℃，试样热膨胀系数略有升高，但幅度不大，基本可认为在室温～1 100 ℃区间内材料的热膨胀性能稳定。表4为纵向热膨胀系数预测结果与实测值对比，最大相对偏差为-3.54%，验证了该方法预测三维编织复合材料热膨胀系数的准确性。

表3 试样不同温度α11

图13 试样自由热膨胀位移-温度曲线

表4α11预测值与实验对比

Table 4 Comparison ofα11through prediction and experiment

试验值/10-6·K-11号试样2.402号试样2.54预测值/10-6·K-12.45相对偏差2.08%-3.54%

3 结 论

建立了包含界面层和基体孔隙的三维编织陶瓷基复合材料热膨胀行为计算模型，得到材料各方向热膨胀系数和热应力分布，研究了孔隙参数对热膨胀系数的影响，并开展了纵向材料纵向热膨胀系数测定试验，结论如下：

(1)纤维束单胞有限元法和解析公式预测纤维束纵向热膨胀系数结果相当一致，相对偏差仅为0.56%，界面层对纤维束热膨胀系数的影响不可忽略；

(2)基体孔隙位置的随机分布对热膨胀系数计算结果没有影响，孔隙率的增加会引起纵向和横向热膨胀系数的显著减小，孔隙中的开孔比例对热膨胀系数的影响尚需进一步研究；

(3)纤维束上的热应力水平大于基体，基体与纤维束交界面存在应力集中，基体气孔单元的存在使周边同样存在应力集中；

(4)试验结果表明温度在室温～1 100 ℃区间内材料纵向热膨胀性能较为稳定，热膨胀系数预测结果与实测值较为相符，最大相对偏差仅为-3.54%。

该计算模型能够有效分析三维编织陶瓷基复合材料热膨胀性能，后续可以研究闭孔结构对热膨胀系数的影响规律和机理。