三关节连杆欠驱动手爪参数优化

王福华 ，刘玉旺

（1.中国科学院沈阳自动化研究所，辽宁 沈阳 110016；2.中国科学院大学，北京 100049）

1 引言

欠驱动机构是近代研究发现的一种新型机构，因其驱动元件数小于机构的自由度而得名。欠驱动机械手作为欠驱动机构的衍生物，其不仅驱动元件少，且能够自适应抓取不同形状和尺寸的物体。同时与传统的灵巧手相比较，其生产加工制造成本便宜，结构轻巧，控制简单[1-3]。目前国内外研究学者对于欠驱动机械手的理论研究和实践探索都取得重大的成果。对于连杆欠驱动手爪影响其抓取稳定性的主要因素是连杆结构设计参数。因此在连杆欠驱动手爪的设计阶段，合理地选择设计参数是至关重要的[4-5]。然而，考虑到拓扑优化许多设计参数，例如关节的数量，关节的长度，作用在关节旋转点的扭矩以及在接触点出的接触力等。不能直接简单地用传统的方法来分析设计各个连杆关节的参数[6]。目前大多数研究的文献和成果不能直接应用推广到设计阶段[7-8]。一方面由于设计优化重点在于驱动参数是基于制造和拟人化方面的考虑。另一方面，其理论研究大部分是关于两个关节的简单欠驱动手爪。此外，大多参数设计研究仅限于特定的欠驱动手爪的驱动机构[9-10]。针对三个关节的欠驱动手爪，采用等接触力方法，以传动角和传动比作为参数优化设计的约束条件，确定欠驱动连杆几何设计参数。该方法不仅可以作为参数优化的方法确定欠驱动连杆几何设计参数，同时也适用于多种驱动系统的欠驱动手爪。

2 连杆欠驱动手爪的接触力

在连杆欠驱动机构中，各个关节在接触点处的接触力的大小直接影响其抓取的稳定性和可靠性，同时也是参数优化设计的一个重要的约束条件。接触力分析的目的是计算平衡关节外力所需的驱动力，力矩以及各连杆的受力情况。此处分析忽略各关节的重量和各关节运动副间的摩擦。连杆欠驱动手爪的抓取过程一个连续不间断的过程，各个关节与被抓取物体接触是连续的，为了保证抓取的可靠性。在抓取过程关节与物体全接触。抓取过程中的机构整体受力分析与各个关节受力分析，如图1、图2所示。

图1 抓取过程整体受力分析图Fig.1 Overall Force Analysis of the Grasping Process

图2抓取过程局部受力分析图Fig.2 Partial Force Analysis of the Grasping Process

图1 和图2中首端关节，中间关节，末端关节的力矩分别为T11，T12，T13；R1，R2分别为传动比。

传动比R1，R2不是一个固定的常数值，它是由实际的旋转关节所决定的。对于抓取平衡，各个关节施加在被抓物体对象上的接触力为正压力。各个关节的受力图，如图2所示。

首端关节在接触点的接触力F11，首端关节在旋转点O11处的力矩静态平衡方程如下：

中间关节在接触点的接触力F12，首端关节在旋转点O13处的力矩静态平衡方程如下：

末端关节在接触点的接触力F13，首端关节在旋转点O13处的力矩静态平衡方程如下：T13-F13P13=0 （3）

联立式（1）～式（3）可得：

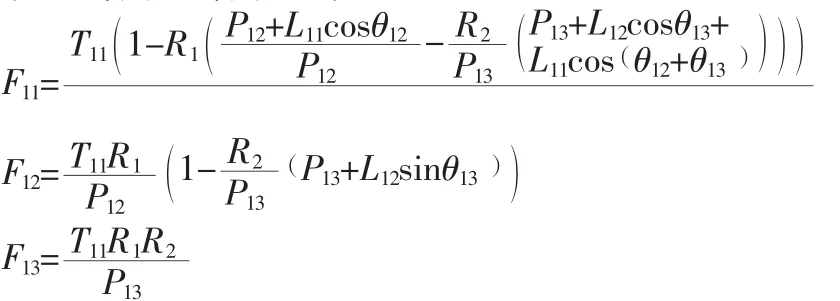
全接触抓取过程中，在各个接触点处的接触力F11，F12，F13必须为正值，即 F11＞0，F13＞0。

超高压萃取法又叫超高冷静压法，它是指在常温条件下，将高压作用于料液中，保持一定的压力后再迅速将该压力卸除，从而达到萃取目的的方法。此法因为十分有效地增大了成分的收率，而被广泛应用于植物和食品有效成分的萃取中。贾春晓等通过正交试验优化了超高压提取法从花椒中提取精油的提取条件，最后得出用超高压法提取花椒精油的最优工艺条件：压力为300 MPa，固液比为1∶40，加压时间为3 min，在此条件下得到的提取率为24.16%，配合GC-MS联用法进行分析，确认了花椒精油中包含67种成分。

末端关节与中间关节的转矩的传动比R2与参数L10，L11，L12，P11及r有关。对于给定的L10，P11值时，稳定状态半径r是仅与L11，L12有关。对于给定值 L10=20mm；P11=30mm 时。R2随 L11，L12，r变化的曲面，如图3所示。

由图3所示，被抓取物体的半径r取不同值时。R2随r的增大而减小的，同时R2max≤0.5。

图3 传动比R2与L11，L12关系Fig.3 Relationship Between Transmission Ratio R2and L11，L12

首端关节与中间关节的转矩的传动比R1与参数L10，L11，L12，P11及r有关。对于给定的L10，P11值时，稳定状态半径r是仅与L11，L12有关。对于给定 L10=20mm；P11=30mm，同理可得 R1max≤1。

3 抓取关节的运动学分析

三关节连杆欠驱动手爪的抓取机构可以看成是由两个四连杆串联构成的。整个机构等价于六杆机构。其机构几何模型示意图，如图4所示。

对于四连杆机构，传动比R1，R2与四连杆的设计参数有关，其中 R1是下部四连杆设计参数 a1，b1，c1，Ψ，θ12的函数；R2是下部四连杆设计参数 a2，b2，c2，Ψ，θ13的函数，如表 1 所示。

图4 欠驱动机构的几何模型Fig.4 Geometric Model of Underactuated Mechanism

表1 R1，R2与设计参数的函数关系式Tab.1 Relationship Between R1，R2and Design Parameters

其中，下部四连杆机构中的关节长度为b1，上部四连杆机构中关节的长度为b2；下部驱动杆的长度为a1，上部驱动杆的长度为a2；上部连杆的长度为d2，下部连杆的长度为d2；下部四连杆机构中的被驱动杆的长度为c1，上部四连杆机构中的被驱动杆的长度为 c2。角度 θ10、θ20、θ30和 θ40分别是 B1O11、O11O12、O12A1、A1B1与X1轴的夹角;角度 θ12、θ22、θ32和 θ42分别是 B1O12、O12O13、O13A2、A2B2与X2轴的夹角。ψ1为中间关节转角相对于首端指节转过的角度，ψ2为末端关节相对于首端关节转过的角度。

4 抓取机构关节的参数优化

夹紧机构关节研究的重点和难点就是要进一步确定连杆机构中各个连杆的长度参数，使得欠驱动夹紧机构能够更好地实现夹紧过程，优化夹紧的工作空间。机构参数优化主要包括两方面的内容：（1）建立机构优化数学模型；（2）数学模型的求解。而数学模型的建立是整个优化设计的关键。

图5 欠驱动上四连杆Fig.5 Upper Four Links of Under-Actuated Mechanism

图6 欠驱动下四连杆Fig.6 Lower Four Links of Under-Actuated Mechanism

如图5、图6所示，上、下部四连杆机构的各个关节间的转角之间的关系推导，如表2所示。

表2 四连杆机构运动学Tab.2 Kinematics of Four-Bar Linkage

对于下部四连杆机构需要确定的设计参数为 a1，b1，c1，d1，a2，b2，c2，d2，Ψ1，Ψ2。式中：b1，b2—首端关节和中间关节的长度；Ψ1，Ψ2—各个关节间的夹角。b1，b2，Ψ1，Ψ2作为设计常量，而其它的机构尺寸参数 a1，c1，d1，a2，c2，d2为待求参数，是设计变量，可表示为x1，x2，x3，x4，x5，x6，六杆机构中优化设计中的六个参数有一个矢量x来表示。

确定设计变量后，然后建立目标函数，优化设计的任务就是要按所求的设计目标，寻求最优的方案，而设计目标一般表达为设计变量的函数即目标函数。由上节可知，为了保证夹紧关节的在接触点处的接触力不为0，同时保证三个关节在接触点处的接触力尽可能的相等。优化的目的使各个接触力之间的差值尽可能的小。因此确定六杆机构的目标优化函数：

确定传动角的约束条件 在机构优化中，设计变量取值的限制范围以及应满足的运动性能或动力性能要求等限制条件。欠驱动夹紧机构的上，下部四连杆的传动角γ1和γ2，如图7、图8所示。在四连杆机构中，传动角γ越大，对机构的传力越有利。在机构运动过程中，传动角γ的大小是变化的，为了保证机构传力性能良好，应使 γmin≥（40～50）°，在受力较大的四杆机构中，应使机构的最小传动角具有最大值。一般来说，选择四连杆机构的传动角范围为（45°，135°），在这个范围内机构的传动效率比较高。下面以下部四连杆机构为例推导传动角约束。下部四连杆的传动角为γ1，如图7所示。

图7 欠驱动上四连杆传动角Fig.7 Transmission Angle of Upper Four Links of Under-Actuated Mechanism

图8 欠驱动下四连杆传动角Fig.8 Transmission Angle of Lower Four Links of Under-Actuated Mechanism

由图7和图8中的几何关系可知：

由上式可知∠B1A1O12随着B1O12的增大而增大，随着B1O12的减小而减小。当θ10-θ40=90°时，B1O12的值达到最大，同时∠B1A1O12值也最大。因此当 θ10-θ40=90°时，B1O12化简为：

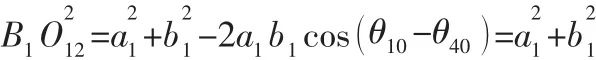
可得：

因此得到下部四杆机构的最大传动角约束为：

即：

当 θ10-θ40接近 0°或者 180°时，∠B1A1O12越小。对于一个给定的四连杆机构，θ10的值是确定的（且 θ10∈（0，π/2）），而 θ40在区间（0，π/2）内取值。所以，当θ40=0，∠B1A1O12最小。

当θ40=0时：

由于上部四连杆在构型上和下部四连杆基本相同，所以上部四连杆的传动角约束可以参照下部四连杆。

确定传动比约束，由上节驱动参数的关系可知传动比0＜R1＜1，0＜R2＜0.5.由几何参数的关系可知传动比R1，R2与连杆长度各参数之间的函数关系，如表3所示。

表3 优化函数的约束条件Tab.3 Constraints of Optimization Function

在Matlab中建立优化设计模型，利用目标优化函数fminunc求解在约束条件下的最优解，如图9所示。

图9 六杆机构的设计参数最优解Fig.9 Optimal Solution of Design Parameters for Six-Bar Mechanism

表4 Fminunc函数优化参数优化结果Tab.4 Optimization Results by Function Fminunc

5 结论

（1）利用力均等原则，保证关节在不同接触点处的接触力保持相等。以力均等为优化目标函数。

（2）在设计三关节欠驱动手爪时，建立六杆机构的运动学方程，以连杆传动角的范围为约束条件对设计参数的取值范围进行约束。

（3）利用Matlab进行目标函数的参数优化，确定设计参数的最优解，得到六杆机构的具体设计参数。