基于直觉灰数集的灰色多属性决策方法
蒋诗泉,刘思峰,刘中侠
(1.铜陵学院 数学与计算机学院,安徽 铜陵 244000;2.南京航空航天大学 经济与管理学院,江苏 南京 210016)
一、引 言
自从Zadeh于1965年提出模糊集理论以来,该理论在各个领域被广泛应用[1]。Atanassov等拓展了传统的模糊集理论,提出直觉模糊集(intuitionstic fuzzy set,IFS)和区间直觉模糊集[2]。随着对直觉模糊集理论研究的深入,成果越来越丰硕。廖虎昌等对直觉模糊信息的集成理论进行了系统研究,其研究成果在多属性决策问题中得到广泛应用[3-4]。随着理论研究和应用研究不断扩展,学者们提出了犹豫模糊集(Hesitant fuzzy set,HFS)和区间犹豫模糊集(Interval hesitant fuzzy set,IVHFS)[5]。灰理论主要以“部分信息已知,部分信息未知”的“少数据、贫信息”不确定性系统为研究对象[6]。由于实际问题的背景、获取信息手段和方法等具有复杂性,所以获取信息同时包含模糊性和灰性等复杂不确定性。为此有研究者试图将灰理论与模糊理论进行有机融合与集成。现有研究集中在两个方面:一是直觉模糊理论与灰色关联度模型有机集成构建决策模型,刘勇等构建了一种动态的区间直觉模糊数的灰色关联度决策模型,李鹏等针对决策信息为直觉模糊数时,提出一种基于灰色关联分析和MYCIN不确定因子灰色直觉模糊的决策方法[7-8]。Zhang提出了一种基于梯形直觉模糊数的灰色关联投影决策方法[9]。二是将直觉模糊理论与灰色预测和灰色聚类模型进行集成,向鹏成等将直觉模糊层次分析法和灰色聚类方法结合,提出基于灰色直觉模糊层次分析法的风险评价模型[10]。李鹏等基于灰数“核”与“灰度”的内涵,将直觉模糊数的犹豫度和记分函数结合构建了直觉模糊数序列GM(1,1)预测模型,从而实现了直觉模糊数的预测[11]。这些研究不但不成体系而且处于初级阶段,没有实现理论的深度融合,很多理论有待进一步探究。在实际决策问题中犹豫模糊信息、灰信息和模糊信息往往相互渗透,很难准确界定。为此,Li等提出了灰色犹豫模糊集,把灰集看作是灰色犹豫模糊集的一个拓展[12]。由于信息受多源因素的影响,常表现为复杂不确定性,为精确描述复杂不确定信息,刘思峰教授提出了一般灰数的概念,从而解决复杂信息的准确表征问题,但是由于一般灰数结构复杂,所以其运算法则、距离测度和排序等问题都没有得到很好的解决[13]。也有学者基于灰数的内涵和产生的背景,构建了一般灰数距离测度公式及相应的决策模型[14-16]。为有效克服一般灰数运算系统没有被满意解决这一现状,本文试图规避一般灰数的运算,利用灰数可能度函数和模糊集成理论等方法,定义直觉灰数(intuitionstic grey number,IGN)和直觉灰数集(intuitionstic grey set,IGS),将一般灰数中每个小区间灰数用一个直觉灰数来表征,一般灰数就被等值转换为一个直觉灰数集。为此,本文定义了两个直觉灰数集之间的运算,以便实现一般灰数运算的转换,在此基础上分析了直觉灰数的运算法则、集成算子、距离测度等内容。最后,利用一个实际决策案例,通过方法比较,验证了该方法的科学性、合理性和可行性。
二、一般灰数及直觉灰数基本理论



定义4:用来描述一个灰数取某一数值的“可能性”,或某一具体数值为灰数真值的“可能性”的连续函数称为灰数可能度函数。其中,取某个值的可能性大小习惯记为P(⊗i),常用一个规定起点、终点确定左升、右降的连续函数为典型可能度函数。
在实践运用时,为了编程和计算方便,多数情况下L(x)和R(x)简化为直线方程,所以其典型灰数可能度函数如图1所示:
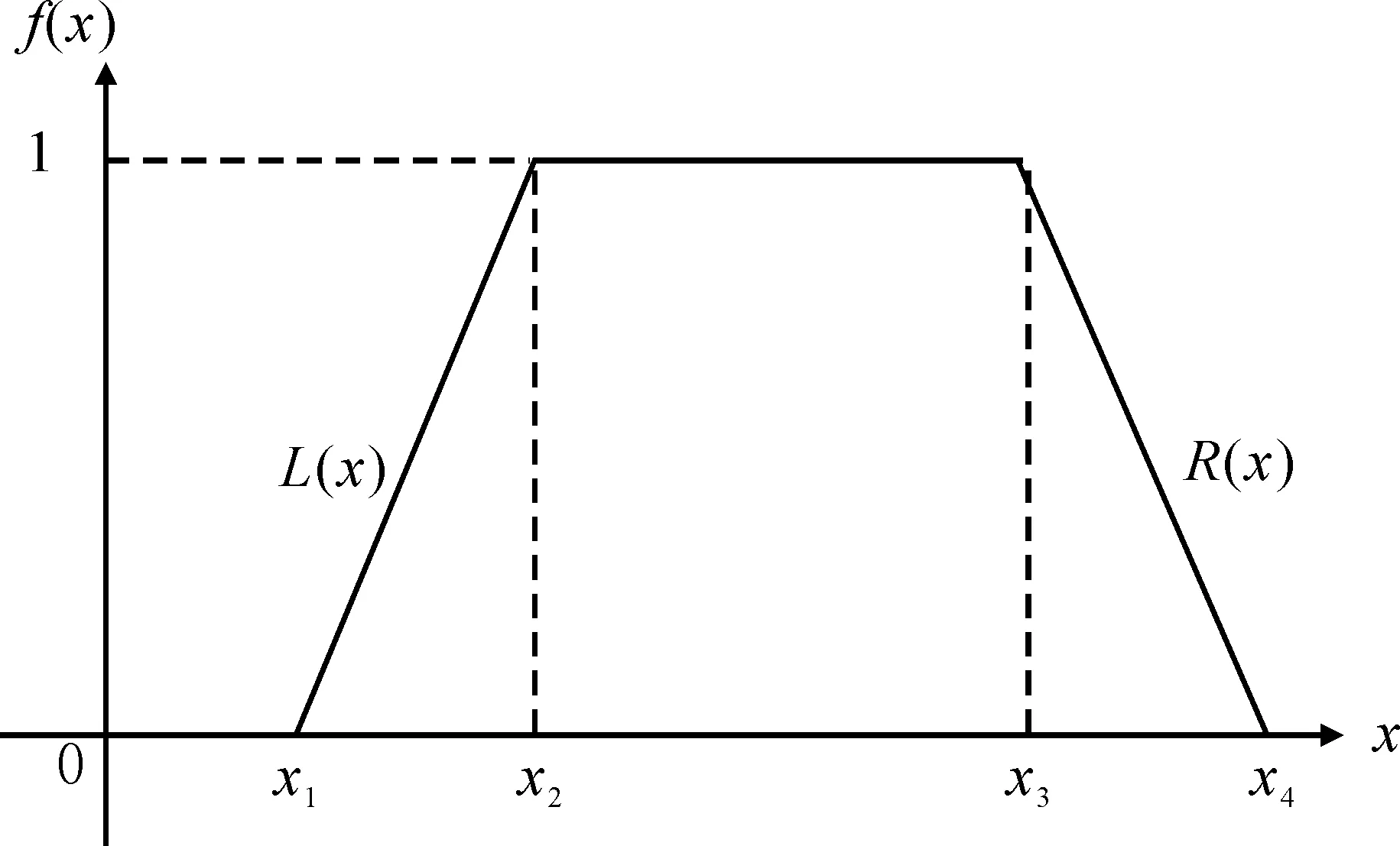
图1 典型灰数可能度函数
其一般的数学表达式为:

定义5建立了一般灰数与一个直觉灰数集等值转换的方法,也表明可以将直觉灰数看作一般直觉模糊数的扩展,直觉灰数集理论也是一般直觉模糊理论的拓展。从而实现了灰理论与模糊理论的有机融合,利用灰理论来解决模糊理论中“少数据、贫信息”的不确定性问题。
三、直觉灰数的运算法则与集成算子理论
利用t-conorm公式Sp(x1,x2)=x1+x2-x1x2和t-norm公式Tp(y1,y2)=y1y2具有单调递增性有界性等和灰数的灰度不减原则,定义直觉灰数的运算法则与直觉灰数的集成算法理论。
定义6:设α=(P(⊗i),go(⊗i)),α1=(P(⊗1),go(⊗1)),α2=(P(⊗2),go(⊗2))为直觉灰数,则
1.α1∩α2=(min(P(⊗1),P(⊗2)),max(go(⊗1),go(⊗2))
2.α1∪α2=(max(P(⊗1),P(⊗2)),max(go(⊗1),go(⊗2))
3.α1⊕α2=(P(⊗1)+P(⊗2)-P(⊗1)P(⊗2),go(⊗1)go(⊗2))
4.α1×α2=(P(⊗1)·P(⊗2),go(⊗1)+go(⊗2)-go(⊗1)·go(⊗2))
5.λα=(1-(1-P(⊗))λ,go(⊗)λ),λ>0
6.αλ=(P(⊗)λ,1-(1-go(⊗))λ),λ>0


定理2:经过由IGWA的算子作用后的直觉灰数满足广义灰度不减公理。


四、基于直觉灰数集的一般灰数距离测度
通过定义5实现一般灰数与直觉灰数集之间的等值转换,以此为基础定义一般灰数间的距离测度的一般性公式。


证明:(略)。
五、基于直觉灰数集的灰色多属性决策方法步骤
在一般灰数代数运算系统还没有满意解决的前提下,通过把一般灰数等值转换为直觉灰数集,实现科学决策,提高决策的精准度。同时,该方法可以规避一般灰数间比较和指标规范化处理等运算问题。
STEP1:基于灰数可能度函数构造原理,并结合实际问题背景,构建灰数可能度函数;
STEP2:将一般灰数表征的决策信息等值转换为含直觉灰数的直觉灰数集表征;
STEP3:将每个属性指标的直觉灰数集转换为一个直觉灰数;
STEP4:求出最优理想方案及相应各属性的直觉灰数值;
STEP5:求每个方案与最优理想方案的距离,并进行排序,距离值越小,方案越优。
六、应用案例分析
随着人们对物质生活和健康的意识提升,老年保健品生产企业现有产品功能已经不能满足中老年人群需求,出现了难于销售,经济效益下降等现象,经公司高层研究决定,拟准备研发功能齐全的保健品,在产品研发之前,首先,公司确定由市场部进行研发前的市场前期调研。为了保证调研数据真实性,分两队人员对拟开发的三种类型产品进行独立前期调研。其次,组成专家论证组将两队调研结果进行综合分析后。最后,用产品销售量、产品市场占有率、产品开发成本三个指标对三种类型产品进行评价,根据评价排序结果,选择一种产品进行投资。由于不同调研队对同一指标所获得结果不一致,为了精确地表达这些决策信息,本文采用一般灰数将其信息表征出来。为了简化起见,将案例简述为:一家企业,现要在这三种产品A1,A2,A3中选择一种产品进行开发投资,其评价指标分别为:S1表示产品销售量,S2表示产品市场占有率,S3表示产品开发成本,指标权重为W=(w1,w2,w3),经专家评价三个指标的权重范围为w1∈[0.2,0.4],w2∈[0.2,0.5],w3∈[0.1,0.3],具体指标数据见表1,三个评价指标的讨论域分别是[0,20],[5,25],[80,130]。分析该企业如何在这三个产品中选择一款产品进行开发投资。

表1 决策矩阵
STEP1:根据本问题的实际情况,结合可能度函数的构造原理,通过多轮专家讨论,确定三个属性指标的可能度函数分别为:
STEP2:将方案的每个指标的一般灰数值转换为直觉灰数集。
项目(方案)A1中的S1={〈0.916,0.1〉,〈0.833,0.1〉},S2={〈0.938,0.05〉,〈0.889,0.1〉},S3={〈0.934,0.06〉,〈0.7,0.1〉};
项目(方案)A2中的S1={〈0.75,0.1〉,〈1,0.1〉},S2={〈0.75,0.1〉,〈0.909,0.1〉},S3={〈0.652,0.2〉,〈0.9,0.1〉};
项目(方案)A3中的S1={〈0.792,0.15〉,〈0.833,0.1〉},S2={〈0.75,0.1〉,〈0.818,0.1〉},S3={〈0.435,0.2〉,〈0.913,0.12〉}。

项目A1的各属性集成为直觉灰数分别为:
S1=〈0.916,0.1〉⊕〈0.833,0.1〉=〈0.882,0.099〉,S2=〈0.938,0.05〉⊕〈0.889,0.1〉=〈0.917,0.071〉,S3=〈0.934,0.06〉⊕〈0.7,0.1〉=〈0.896,0.077〉。
类似地,项目A2中的各属性集成为直觉灰数分别为:
S1=〈0.5,0.099〉,S2=〈0.849,0.099〉,S3=〈0.814,0.099〉。
项目A3中的各属性集成为直觉灰数分别为:
S1=〈0.814,0.122〉,S2=〈0.787,0.099〉,S3=〈0.902,0.155〉。
将各方案指标属性的直觉灰数值用一个矩阵表示,详见表2。

表2 集成直觉灰数信息矩阵
STEP4:求出理想方案及相应各属性的直觉灰数值。按照可能度值取最大,灰度值取最小确定理想方案,并记为A+。
A+=(〈0.882,0.099〉,〈0.917,0.071〉,〈0.902,0.077〉)
STEP5:求每个方案与理想方案的Euclidean距离,把每个方案的所有指标属性的直觉灰数值看作一个直觉灰数集,利用直觉灰数集之间的Euclidean距离公式进行计算,即

计算各方案与理想方案的距离:
同理,可以计算出d(A+,A2)=0.162 1;d(A+,A3)=0.069 4。按照与理想的距离对各方案进行排序为:A1≻A3≻A2。
为了说明该方法的科学性和合理性,本文利用刘中侠等人的广义灰数的双向投影灰靶决策方法对方案也进行排序选优。他们的方法排序为A1≻A2≻A3,本文中利用各备选方案与理想之间的距离排序为A1≻A3≻A2。本文与刘中侠等人研究中排序不完全一致,但是两种方法的最优方案是完全一致的。他们是以基于“核”与“灰度”,构建一般灰数距离及的运算规则。本文是基于灰数“核”的可能度函数和“灰度”理论,构建直觉灰数和直觉灰数集,计算各方案与理想方案的距离并按距离进行排序,避免了一般灰数的运算[16]。
七、结论及启示
复杂不确定性问题的研究是灰色理论研究的热点领域,主要包括复杂不确定信息的表征、复杂不确定信息的运算、灰色不确定信息下的建模技术、几类不确定性理论的深度融合等问题。本文将灰理论与模糊理论两个不确性理论进行融合研究,将灰数“核”的可能度函数与“灰度”的理论和直觉模糊理论与集成理论进行深度融合,构建直觉灰数和直觉灰数集,并构建一般灰数与直觉灰数集等值转换的方法、直觉灰数的运算法则、直觉灰数的集成算子、距离测度等内容。在此基础上构建了基于直觉灰数的灰色多属性决策模型及决策步骤,并利用一个实际应用案例验证了该决策模型可行性与合理性。本文中直觉灰数(集)理论既能利用一般灰数在信息表征上的优点,又规避一般灰数运算系统不完善所产生的计算误差和信息丢失等问题,为研究一般灰数信息下决策、预测、控制、动态规划、聚类评估、博弈等模型提拱了一个全新研究视角。

