一类MHD方程组的加罚逼近方法

张 超

(温州大学数理与电子信息工程学院，浙江温州 325035)

磁流体力学（Magneto Hydro Dynamics，MHD）方程组描述了导电流体在磁场中运动所遵循的物理规律，是用来研究运动的导电流体和磁场相互作用中各物理量间的变化关系以及电磁场和速度场中各物理量的分布的，在天体物理学和地球物理学、核反应堆中的液态金属冷却、金属的电磁铸件等领域有广泛的应用．关于 MHD方程组的物理背景，可以参考 Hughes[1]和 Moreau[2]的相关文献．

MHD方程组是由流体力学的Navier-Stokes方程和电动力学的Maxwell方程所耦合的非线性偏微分方程组，求解非常困难和复杂，人们往往通过数值模拟来了解MHD方程组解的特征．随着计算机技术的不断进步和发展，不可压缩MHD方程组的数值模拟也得到了全面的发展，并且理论研究和数值模拟相辅相成．研究不可压缩MHD方程组的数值方法一直是国内外计算数学界和应用数学界广泛关注的热点问题之一，有大量的文献研究定常或非定常MHD方程组解的适定性[3-4]和数值方法[5-18]．

本文考虑如下的MHD方程组：

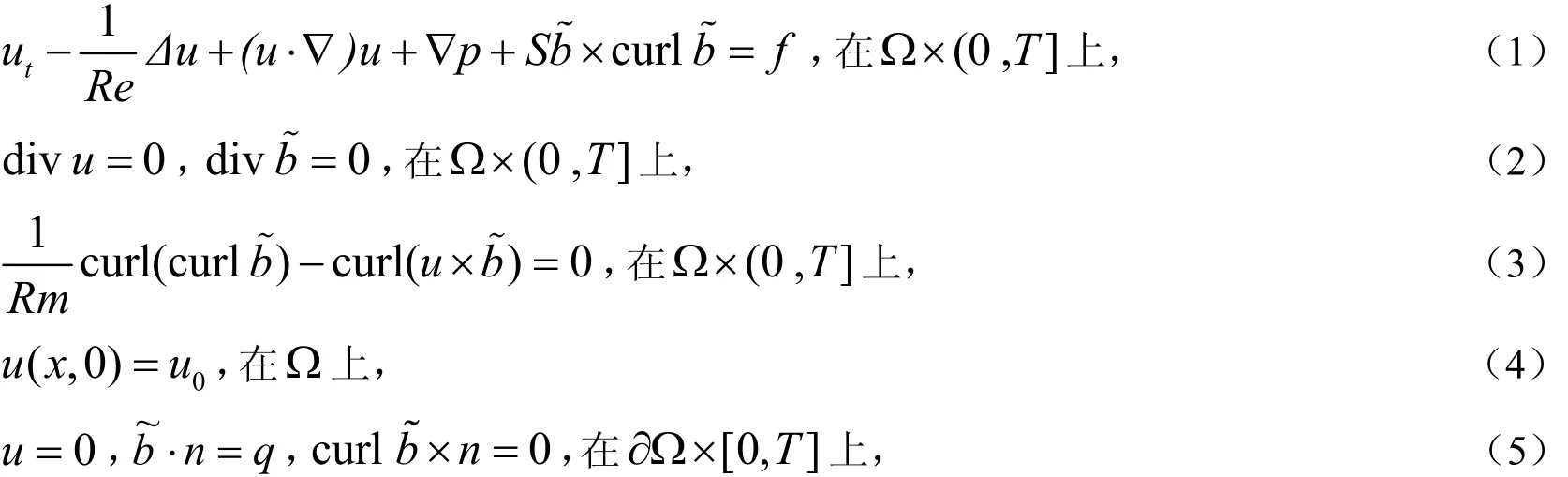
方程组（1）–（5）是Gerbeau和Bris在文[19-20]中首先研究的，并证明了在物理数据足够小的假设下局部强解的存在唯一性；Li等在文[21]中研究了求解该方程组的解耦半隐算法，在理论上分析了算法的稳定性和收敛性，并给出了算法的有限元误差估计．本文的主要工作是引入加罚参数ε，建立原方程组（1）–（5）的加罚逼近系统，并给出原方程组的解与加罚逼近问题的解关于ε的误差估计．本文工作的主要意义是通过建立原方程组的加罚逼近系统的解来构造求解原方程组解的数值迭代算法．

1 预备知识

首先，引入一些函数空间及相关的范数．当k ∈ N+，1≤p≤+∞时，记Wk,p(Ω)为Sobolev空间，其范数定义如下：

那么存在仅依赖凸区域Ω的常数C1＞0，使得对wW∈有：

当2≤p≤6时，利用Sobolev不等式有：

这里C2C3,是仅依赖Ω的正常数．定义三线性项

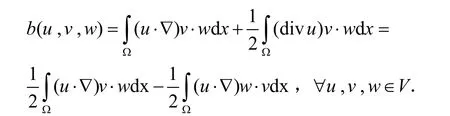
这组新的MHD方程组（10）–（14）解的存在唯一性在文献[19-20]中已经得到证明．

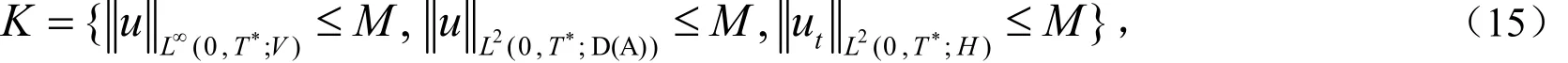
还需要下列正则性．

定理2[21]在定理1的假设下，存在常数 C ＞ 0 使得

这里常数C与 Ω , R m,Re相关．

2 加罚逼近

这一节将建立方程组（10）–（14）的加罚逼近系统：

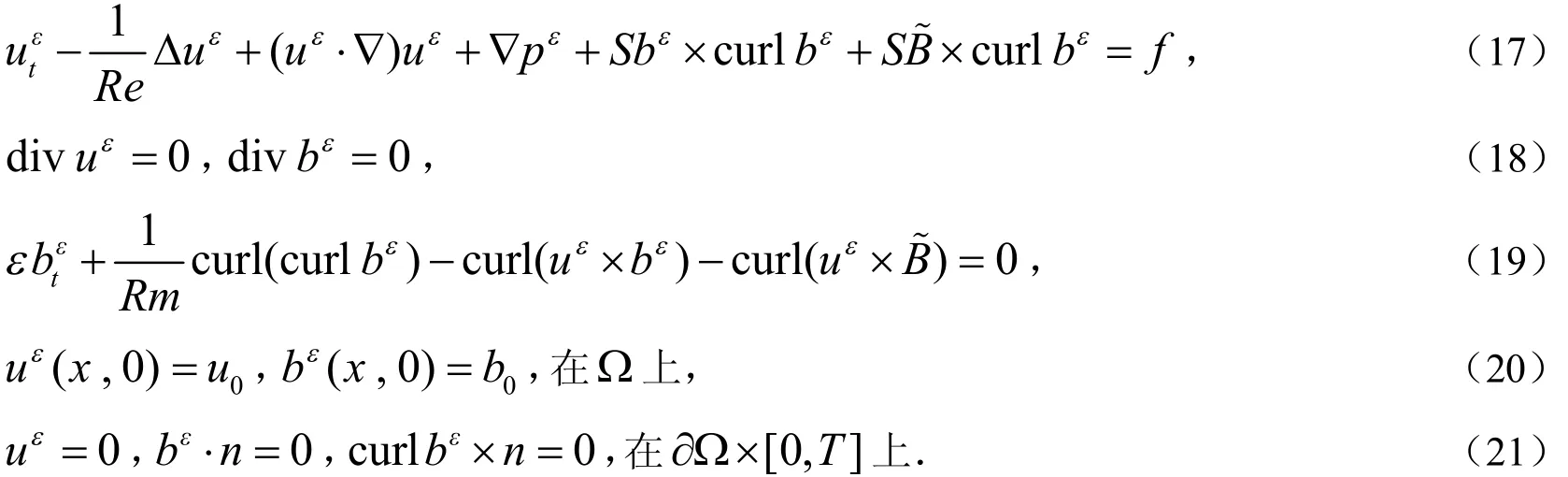
这里ε＞0为小参数．

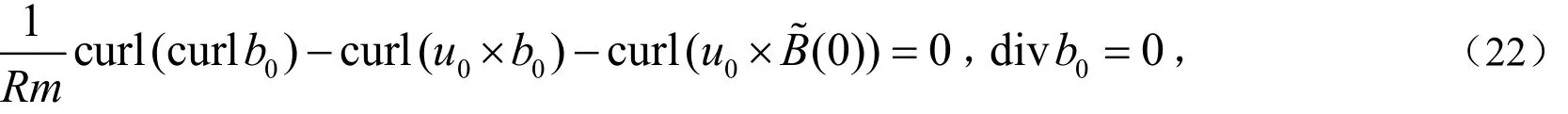
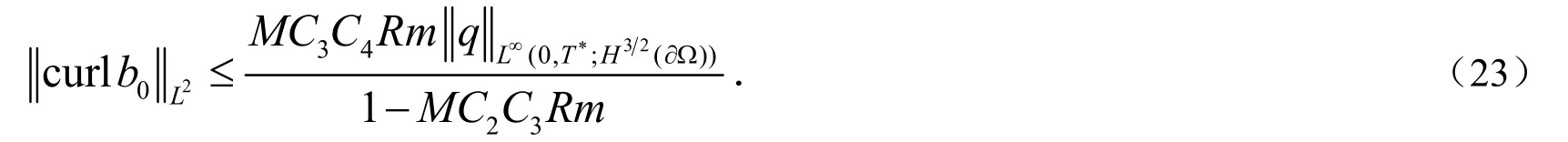
当ε=1时，加罚系统（17）–（21）为非定常不可压缩MHD方程组，其弱解(uε,bε)的存在性在文[4]中已经得到证明．本文主要给出(uε,bε)与MHD方程组（10）–（14）的解(u,b)关于加罚参数ε的误差估计．首先，关于和我们有如下的先验估计．

引理2 在定理1的假设下，存在常数C＞0 使得

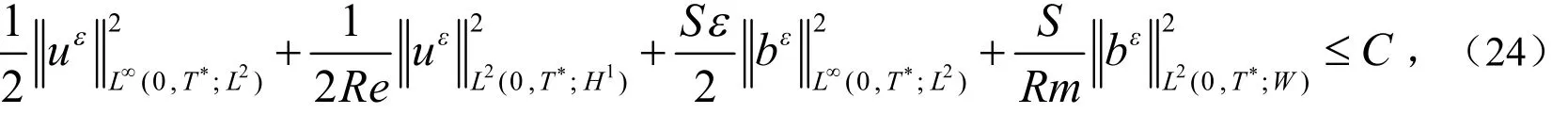
证明：用,uεSbε分别检验（17）式和（19）式，有：

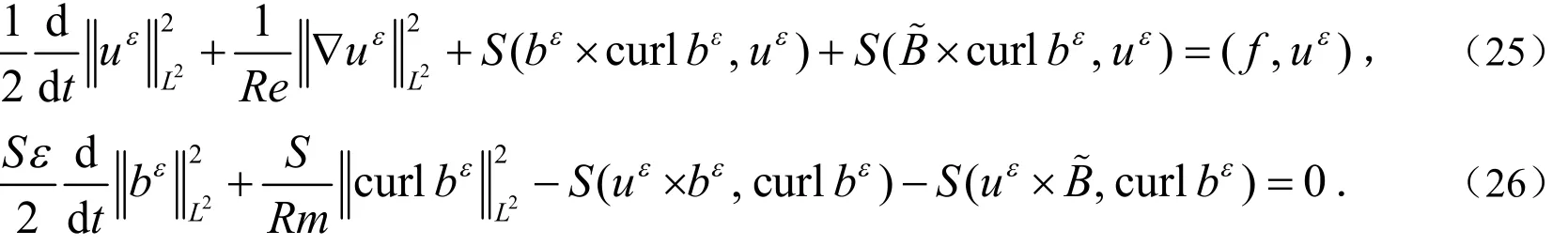
将（25）式和（26）式相加有：

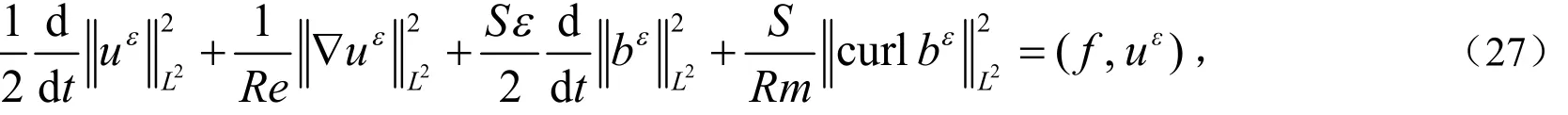
这里用到了

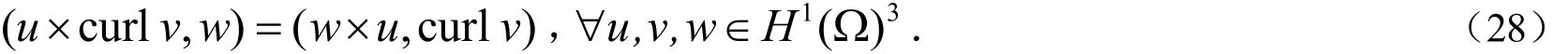
再（27）式右边利用Young不等式有：

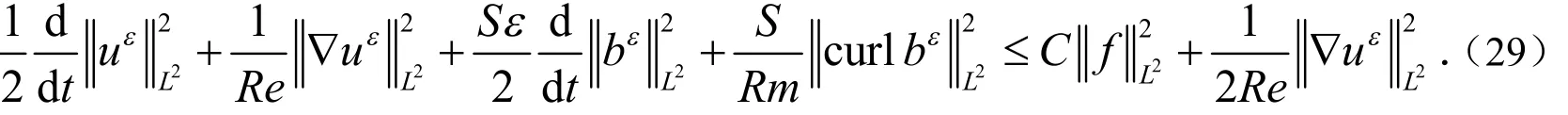
将（29）式关于时间从0到t ＜T*进行积分，那么存在常数 C＞0使得

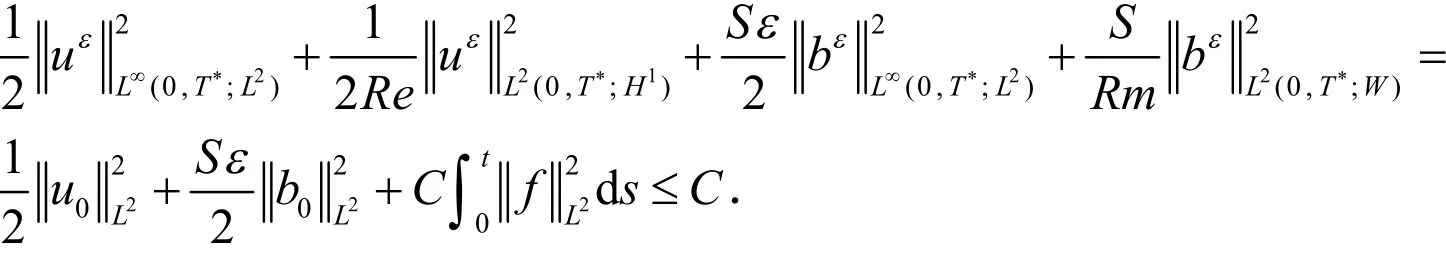
证毕．

3 误差估计

本文的主要结论如下：

定理3 在定理1的假设下，存在常数 C＞0 使得

证明：将（12）式左右两边同时加上εbt，有：

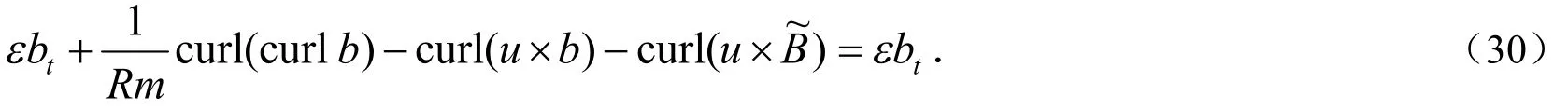
等式（10）和（30）分别减去（17）式和（19）式，有：

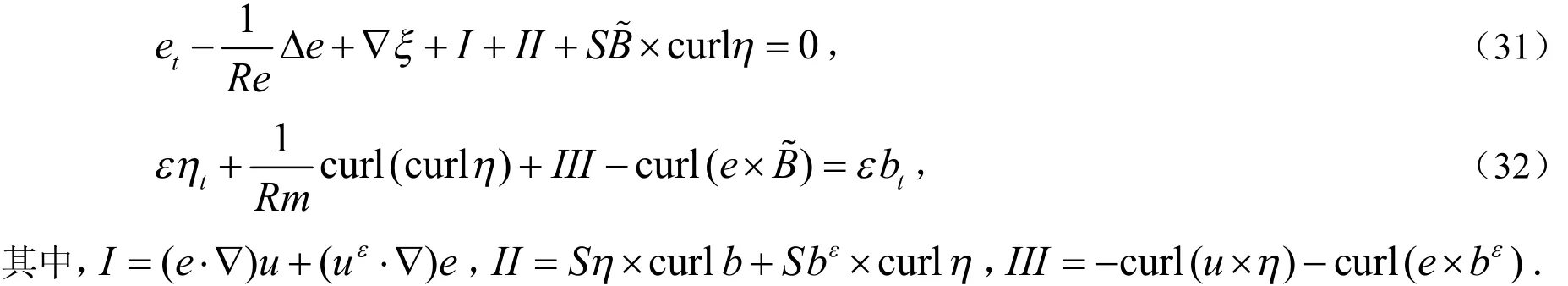
e与（31）式两端作内积有：

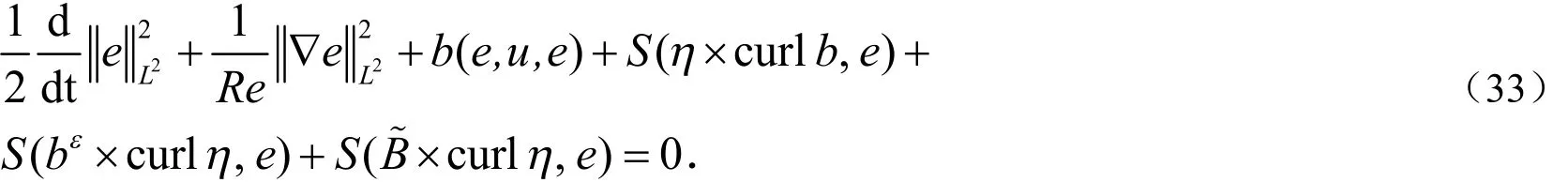
Sη与（32）式两端作内积有：

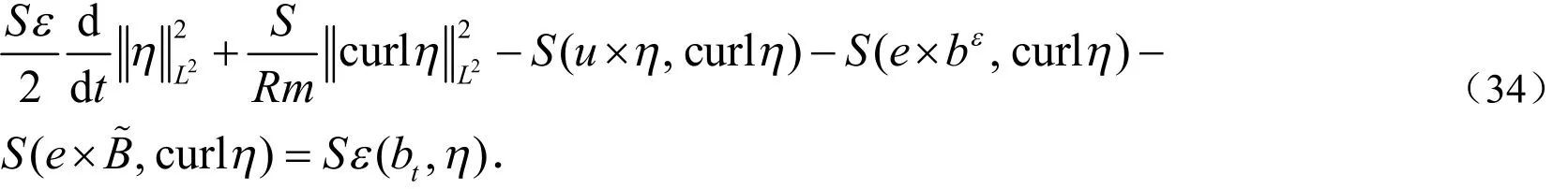
将（33）式和（34）式相加，并利用（28）式得：

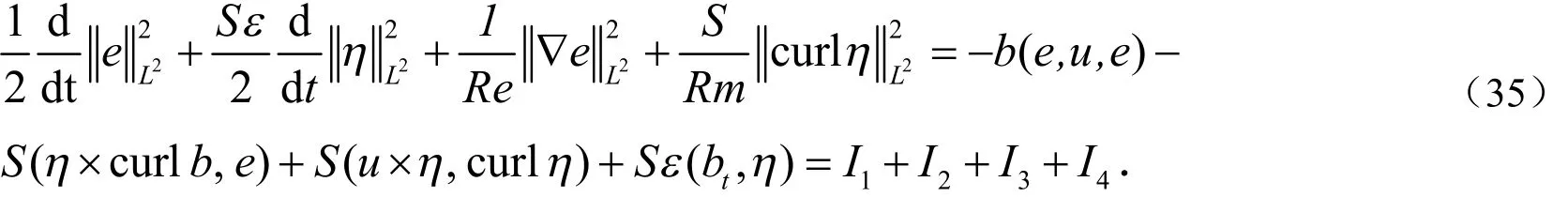
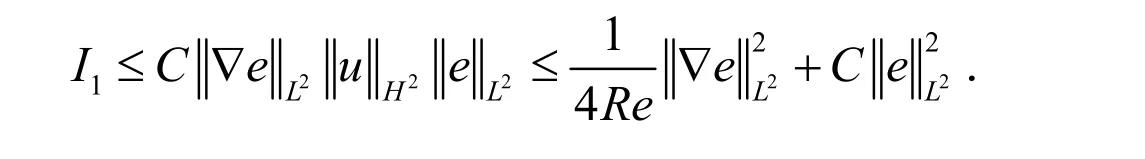
类似地有：

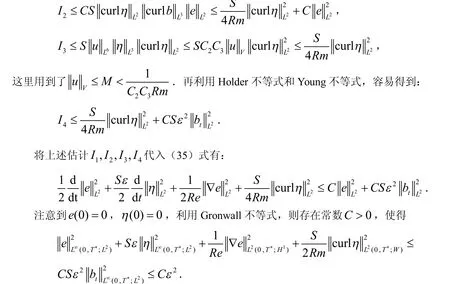
证毕．