基于CNN提取特征进行标签传播
刘新伟,陈楷哲,张振宇,姜贺云
(温州大学数理与电子信息工程学院,浙江温州 325035)
图像分类是计算机视觉的核心任务,比如对象识别、图像标注、行为识别等均可转换为图像分类问题[1].本文考虑RGB图像,它通常被表示为三维数组,其数据类型为uint8.对于图1,图案是狗还是熊,对于人类来说,这是一个十分简单的问题,但计算机无法直接给出判断,因为计算机仅仅可以识别像素级别的数字特征,无法直接解读图片的具体语义,即使是顶级的程序员也无法直接编写出判定所给图片是猫还是熊的程序.为此,人们逆向思考,借助人类自己的判别能力优选出大量图片并对其手工标注,然后,设法去拟合图片的像素级别的特征与其标签的关系,由此而产生了许许多多的用数据去编程的优秀算法.
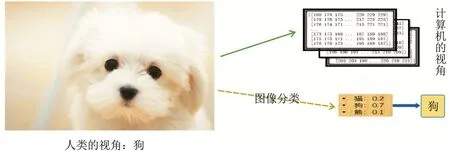
图1 人类和计算机对图像辨别的差异
近几年来,以卷积神经网络[1](CNN)为代表的深度学习技术在计算机视觉方面取得了许多远远超出普通的机器学习算法的傲人成绩,更甚者,部分使用CNN进行图片分类的精度也超出了手工标注获得的精度[2].卷积神经网络经历了 LeNet[3]、AlexNet[4]、VGG[5]、GoogleNet[6](Inception)、ResNet[7]、Densnet[8]等变革,变得越来越深,同时训练难度也不断变大.考虑到计算设备、数据集的规模等的制约,迁移学习在计算机视觉中扮演的角色也越来越重要,同时半监督学习对于图片分类任务也是至关重要的,但是仅仅使用浅层机器学习进行标签传播远远无法满足当今社会的需求,由于传统方法通过手工提取的特征泛化性不好,本文将采用深度学习技术提取高级特征,然后再利用高级特征去改进标签传播算法.
1 相关工作
1.1 深度学习模型
从技术角度来看,CNN是一种至少包含一个卷积层(有滤波器的作用)的神经网络.一般地,一个神经元可以看作是线性映射与非线性映射的组合,而多层神经网络是由多个神经元按照分层结构组合而成的.神经网络模型的优化大都是基于反向传播算法完成的.本文使用了He等人[7]提出的残差网络(ResNet),ResNet网络的基本单元是残差块,见图2.

图2 残差模块示意图
ResNet中指出神经网络的训练存在退化问题,即层数加深到一定深度之后,越深的网络训练效果越差,但这并不是梯度消失和梯度爆炸引起的问题(因为已经有许多方法来解决梯度传播的问题).数据经过两条路线,一条与普通神经网络类似,另一条实现了单位映射的路线(被称为shortcut),这两条路线一般被称为“残差块”,在网络中使用残差块的神经网络被称为ResNet.ResNet很好地应对了网络退化问题,可以使网络变得很深.
1.2 降 维
降维是指提取高维空间的关键信息,并将高维空间的问题转换到易于计算的低维空间进行求解的过程.降维是十分必要的,因为它缓解了以下三种问题.
1)多重共线性.预测变量之间相互关联,这样会导致模型解空间的不稳定性.
2)高维空间的稀疏性.高维空间的数据往往是稀疏的,增加了模型求解的难度.
3)过高的维度可能含有大量的冗余信息,妨碍人们找到变量之间真正的隐含信息.
本文主要涉及两种降维方法,无监督的PCA[8]和有监督的LDA[9].下面逐一介绍.
1.2.1 主成分分析法(PCA)
主成分分析法(Principal Components Analysis, PCA)[9]将输入数据x正交投影表示为z,目的是学习该正交投影,使得降维后的数据尽可能地保留原数据空间的信息,通常A被称为解码矩阵,且TA 被称为投影矩阵.为了保留原始信息,需要保证最近重构性或者最大可分性,这样原问题可以转换为:

其中,λ是拉格朗日乘子.这样将X进行标准化处理,那么 XTX可以看作是样本的协方差矩阵;再对 XTX进行特征值分解,并求得最大的p个特征值所对应的特征向量(在 PCA算法中,一般称为主成分)则便可得到A*= ( a1, a2,… ,ap).因而,对于任意的 xi,便可得到其低维表示
1.2.2 线性判别分析(LDA)
线性判别分析(Linear Discriminant Analysis, LDA)[10]的核心思想是设法将样本投影到一个子空间上,且使得同类样本投影后尽可能地接近而不同类样本投影后尽可能地分开.LDA与PCA十分相似,PCA试图找到方差最大的几个主成分,LDA的目标是发现可以最优化分类的特征子空间.
与PCA类似,LDA需要将X进行标准化处理,然后将数据集按其类别划分为c个子集,并计算各个子集类所在集合的均值向量 uj, j = 1 ,2,… , c .构造类间散度矩阵以及类内散度矩阵.不同类之间的样本尽可能分离等价于同类之间尽可能接近等价故而原问题便转换为优化问题因而,取的按照从大到小排列后的前p个特征值所对应的特征向量组成A,最后使用A将样本投影到新的特征子空间中.
1.3 标签传播
半监督学习的算法有很多,本文仅仅考虑标签传播算法.下面构建一个图 G = ( V,E),其中,边集为可表示为一个相似度矩阵[11](,对角矩阵 D = d iag(d1,… ,dm)被称为度矩阵,且称 Δ = D - W 为拉普拉斯矩阵.假定从图G中学得一个映射该映射对应的是分类规则,其中被称为标记矩阵.要实现相似的样本有相似的标记,只需要最小化 E (f ) = T r(FTΔ F )即可.下面公式(2)中分别是按照文[12]对 Δ , F,W ,Y进行分块得到的矩阵,下标 u,l分别代表无标签数据和有标签数据.

2 基于预训练的深度模型提取特征的半监督学习图像分类方法
本文先将 ImageNet(http://www.image-net.org/)数据集上学习的深度模型迁移到 Cifar10(http://www.cs.toronto.edu/~kriz/cifar.html)数据集上,利用深度网络模型提取 Cifar10的深度特征,然后对原深度特征进行降维处理,去除里面的噪声和冗余信息,最后使用降维后的特征来进行半监督学习或者说是标签传播.这样既考虑到了使用深度学习技术提取到的比较好的特征,提高了特征提取的质量,同时也考虑到了无标签数据之间的相似性,且通过降维去除了冗余的特征.具体算法流程如下(对于任意的1im≤≤).
1)找到一个在ImageNet数据集已经训练好的模型,记作Net(本文使用ResNet50),为迁移学习做准备.一般情况下模型Net分为features和output两个部分,分别代表特征提取层和输出层.
2)对于每个样本 xi提取其特征即Net.features为了方便我们仍然将其记作 xi.
3)本文得到的ix的特征维度仍然是比较高的,其中存在着冗余和噪声特征,对其进行降维处理(本文对无标签数据采用PCA,对有标签数据采用LDA),降维后的X记作Z.
4)依据公式(2)对Z进行标签传播获得 Yu,得到无标签样本的预测类别标签,实现无标签图像数据的半监督分类.
3 实验与结果分析
3.1 数据集简介
Cifar10是图像分类问题的基准数据集.Cifar10分为训练集和测试集,它有10个类别,其中训练集包含50 000个样本,测试集包含10 000个样本,且是尺寸为32 × 32的彩色图片,因而数据集足以应对一些中小型模型的需求.类的标记为:airplane、automobile、bird、cat、deer、dog、frog、horse、ship、truck,这些类是完全互斥的,相互之间没有重叠.
3.2 通过CNN提取特征做标签传播的实验与结果
针对Cifar10数据集中的训练集,随机选取由6 000个图像的样本构成的子集作为本论文中的图像分类数据集.在这6 000个样本中,假设部分数据存在类别标签,其它数据无类别标签,构成半监督学习数据集.以分类精确度作为性能度量,并且做一些对比实验.参与比较的方法有作为基准的近邻分类法、基于原始图像像素特征的半监督学习方法以及基于深度特征的半监督学习方法.固定6 000个样本构成的实验集后,每次随机选择有标签的样本,在下面每次实验设置中都要重复10次实验,所得结果的均值和方差在图中均有体现.下面各图中的LGC[12]指的是半监督分类,即使用标签传播做半监督分类,1NN为最近邻分类,GRF[13]指的是高斯条件随机场.
首先固定每类数据中有标签样本数目为50,让半监督学习算法的参数——最近邻数k,从3变化到50,来测试所提出方法对该参数的鲁棒性.图3给出了该实验的结果.从图3可以看出,深度特征数据上的模型的泛化性能显著地好于利用图像的原始像素特征的模型.无论是对数据的原始特征还是深度特征,半监督学习方法的效果都好于有监督的近邻分类方法,较好的最近邻参数选择范围也较广,比如20就是一个不错的选择.
然后,固定邻域范围k = 18,让每类有标签样本的数目从10变化到250,来观察有标签样本数目的变化对分类效果的影响.如图4所示,当每类有标签样本数目为10个时,半监督分类准确率达到50%,当每类有标签样本数目为250个时,半监督分类准确率接近70%,这充分说明了标签数量对图像分类效果的重要性.
总的来说,从图3和图4可以看出,深度学习技术提取特征后再进行半监督学习得到的准确度明显比直接使用原始图像进行半监督学习的准确度要高20% – 30%.更具体是,不管是深度特征还是原始特征,使用1NN(最近邻分类)的分类准确度总是低于LGC[13](半监督分类)和GRF[14](高斯随机场)的分类准确度.总体看来,随着近邻的尺寸(size)或者有标签数据的样本数的增加,分类的准确度均有一定的增幅.
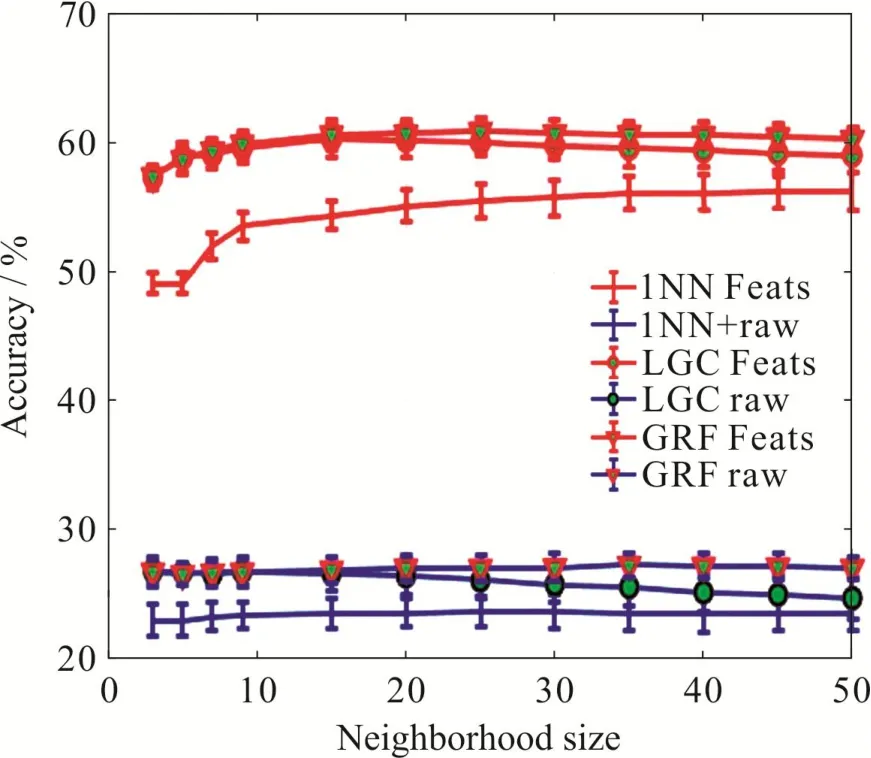
图 3 邻域范围变化的实验结果
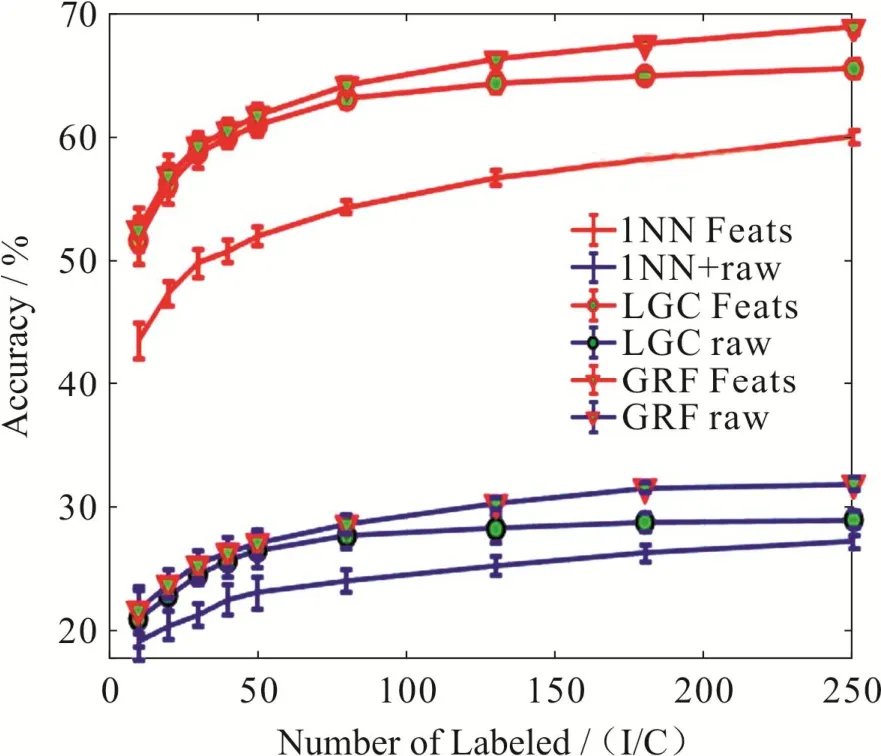
图4 有标签样本的数目从10变化到250的实验效果
接着测试降维方法在去除特征噪声、提高识别效果方面的性能.固定每类数据中有标签样本数目为50,最近邻范围k= 18,图5给出了当PCA降维范围在10到2 000时,半监督分类在深度特征上的效果,图6是图5的局部放大版.可以看出,当PCA维数为200左右的时候,半监督算法给出比较高的准确率,而随着降维维数的升高,算法的性能反而开始下降,直到稳定在和不对深度特征降维的准确率相同.图7给出的是基于有监督数据用LDA方法进行降维的效果.注意LDA方法在9维时能够实现最高的准确率.从图5和图7可以看出,使用降维技术可以使模型分类的准确度提升10%左右.从图7可以看出,有监督降维得到更低的维度空间,可以更加有效地去除信息的冗余,获得更高的分类准确度.
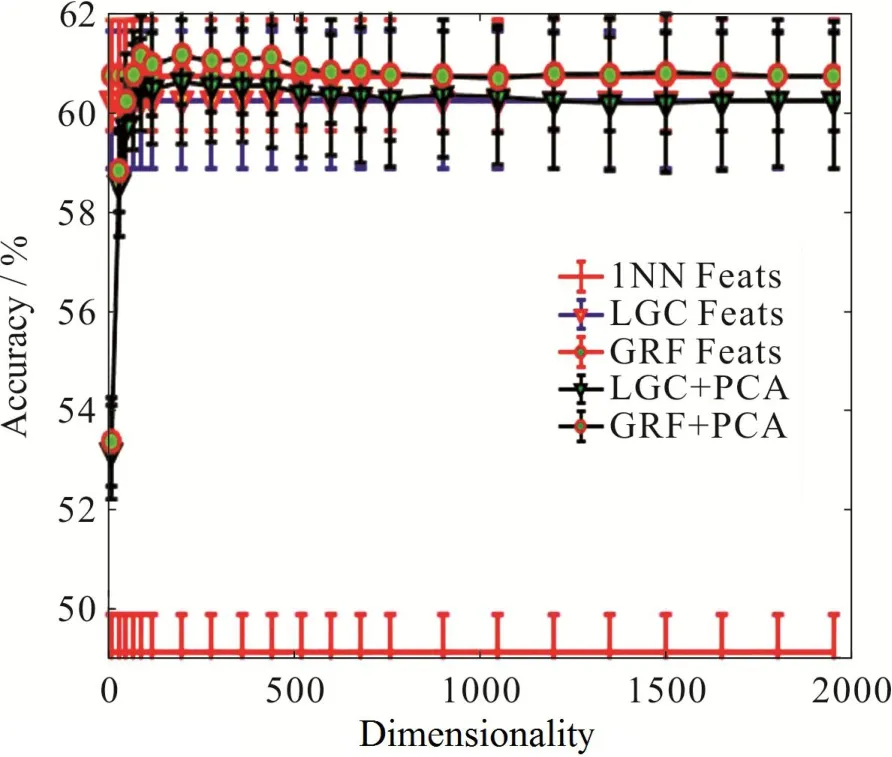
图 5 PCA降维对基于深度特征的半监督算法效果
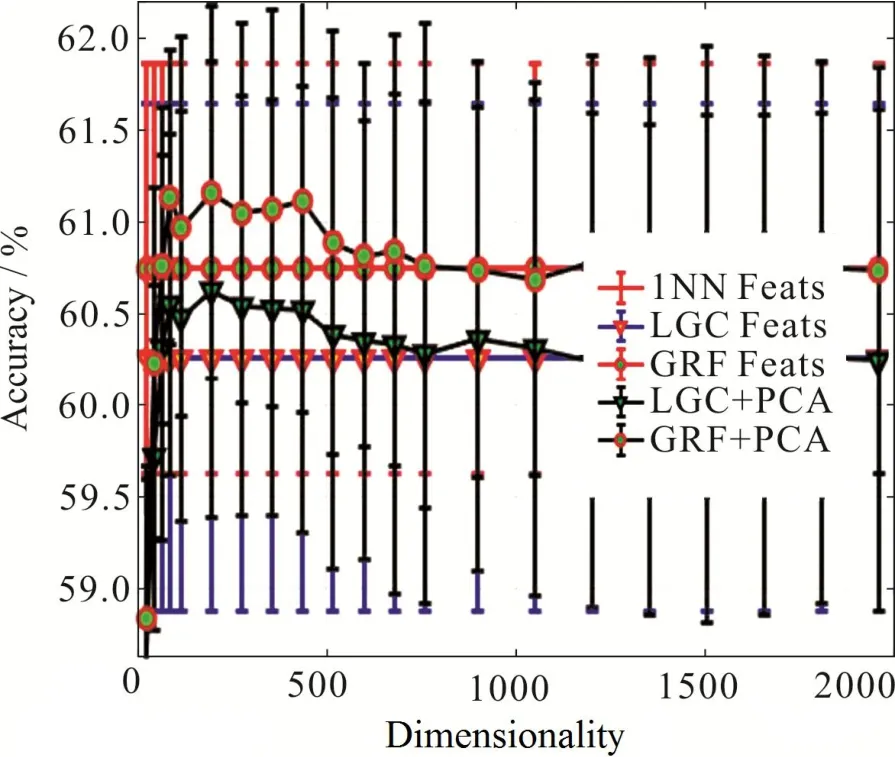
图 6 图5的局部放大图
4 总结与展望
实验结果表明,与直接利用原始像素特征的模型相比,本文提出的算法的性能更高,这说明了深度学习技术相对于浅层机器学习有着很大的优越性.通过上面实验还可以看出,在半监督学习任务中,深度学习技术的使用可以很好地提升分类的准确度,同时,降维技术可以进一步提升深度学习技术的泛化能力.
虽然本文使用深度特征对半监督学习算法——标签传播算法提出了一些改进,但是,由于标签传播本身的计算复杂度是O(m3),这极大地限制了本文算法的进一步改进.进一步拓展本文算法可以从小样本的训练着手.小样本的训练方法有很多,如 One-Shot[15].这样就可以很好地将无标签数据与有标签数据建立联系,从而实现端到端的半监督学习方法.
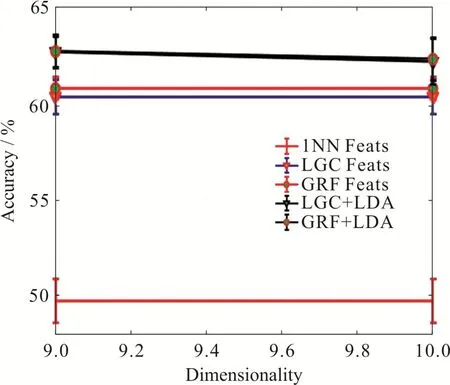
图 7 基于LDA方法降维的深度特征半监督学习效果图

