离散Bose-Einstein方程的全局吸引子与熵的估计
桑燕苗
(温州大学数理与电子信息工程学院,浙江温州 325035)
研究下面耦合的常微分方程组
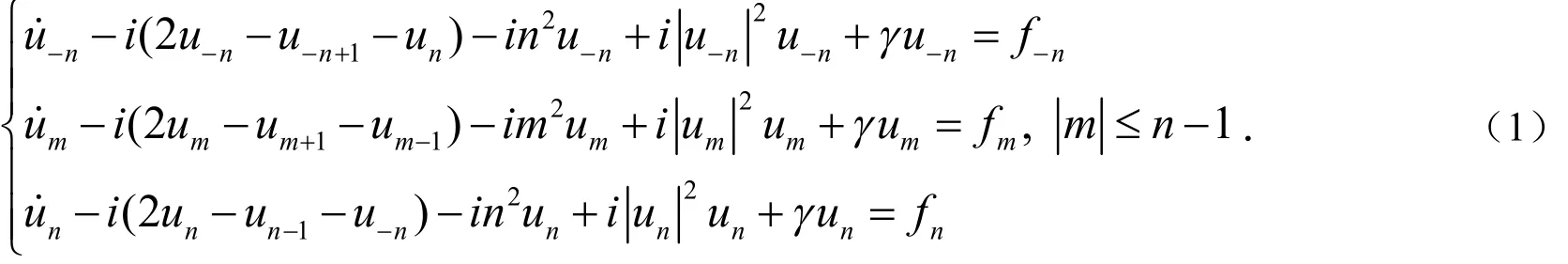
初始条件为


方程(3)是带有弱阻尼和平方势的非线性Schrödinger方程,该方程描述等离子的运动.通常情况下,该方程被称为浓缩的Bose-Einstein方程[1],可从等离子物理或纤维波传播震动中推导出来[2-4].文献[5]证明了该方程在全直线上全局吸引子的存在性,文献[6-7]证明了该方程在二维薄的无界区域上的全局吸引子的存在性与有限维数.
本文讨论了方程(3)在有限格点上的渐近行为,证明了方程组(1)的解算子生成的半群具有全局吸引子,给出全局吸引子的Kolmogorov ε-熵的估计.我们是在有限区间[ ,]nn- 而不是在全直线R上讨论方程(3)的离散近似,是因为方程(3)包含了 ix2u.若在全直线上讨论,该项将产生具有无界系数的项,这将导致解的唯一性得不到证明,从而使得无法应用半群理论来讨论该方程组的解的渐近行为.
1 整体适定性和全局吸引子
对于方程组(1)考虑充分大的自然数n,记

则初值问题(1) - (2)可以写成
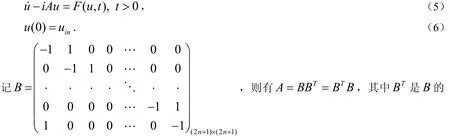
转置.不难验证
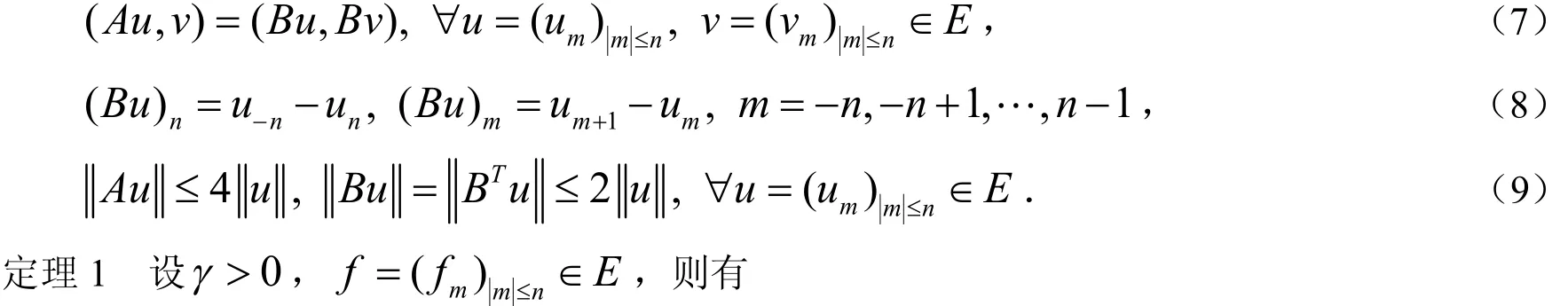
1)局部适定性.对任给的uin∈E,问题(5) - (6)存在唯一解u∈C ( [0,T0),E),其中T0> 0 ,并且如果 T0<+∞ ,
2)整体有界性.对任给的uin∈E,问题(5) - (6)的解满足


证明:
1)注意到常微分方程(5)中包含的算子:AEE↦是线性有界算子,只需验证(,)Fut是从E到E的局部Lipschitz算子.事实上,设R⊂E是有界集.对任意 ,uv∈R,有

应用Gronwall不等式到(15)式有
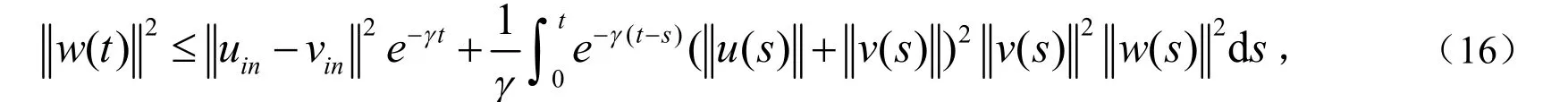
应用Gronwall不等式到(16)式得到

定理1证明完毕.


2 Kolmogorov ε-熵
定义1 对任给的ε>0,记Nε(A,E ) =Nε(A)为E中半径不超过ε>0的覆盖全局吸引子A所需的球的最少个数.定义 Kε(A) = Kε(A,E ) = l n Nε(A)为全局吸引子A的 Kolmogorov ε-熵.

① Lorentz G, Golistschek M. Constructive approximation: advanced problems [M]. Beijing: World Book Press, 2015.


3 结 论
证明了问题(5) - (6)在空间E中是整体适定的,且该方程组解算子在空间E中生成一个连续半群,该半群满足紧性、不变性、吸引性,故半群存在全局吸引子,并通过截断估计给出了全局吸引子的Kolmogorov ε-熵的上界估计.

