平面上的一类扩张流

许卫丽

(温州大学数理与电子信息工程学院，浙江温州 325035)

在过去的几十年里，曲线的发展问题受到了很大关注，其中较为经典的一个曲线流如下：

它是一种周长和所围成的面积都随着时间的增加而减小的曲线流，也即是一种收缩流．Gage等[1-3]在此基础上研究了平面上的其他封闭凸曲线，这些曲线流在有限的时间内收缩到一个点．近几年，人们通过改变曲线流的速度，也即是说通过把等式（1）中的曲率κ改成由曲率、曲线的长度和曲线所围成的面积构成的函数，从而创造出各种各样的曲线流[4-8]．此外，文献[9-13] 还介绍了其他情况的曲线流．最近的一篇文献[14]介绍了一种由保长度的曲线流和一种保面积的曲线流组合成的曲线流．很自然地，我们就会想到能否把前人研究的一种保长度的曲线流与另一种其他的曲线流组成新的曲线流．据此，本文用文献[7]中的保长度的曲线流和文献[15]中的一种周长以及所围成的面积都随着时间的增加而增大的曲线流组合成新的曲线流，具体如下：

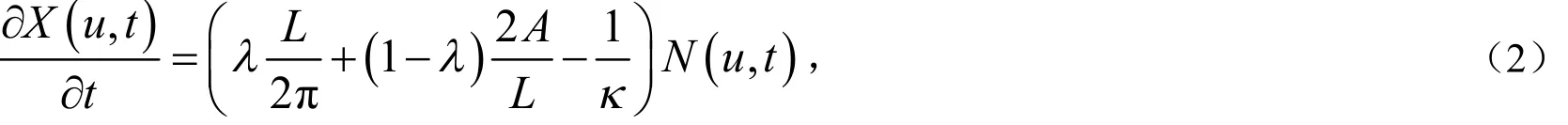
其中0≤λ≤1，初始曲线的方程为X（u , 0）= X0（u）．

定理1 假设 X0（u）是平面上的光滑且封闭的凸曲线，对于任意的时间 t ∈ ［ 0, + ∞ ），方程（2）的解存在且保持凸性．曲线的长度和曲线所围成的面积都是随着时间的增加而增大，且它们都有上界．当时间t→+∞，曲线 X （u, t）在C∞范数下收敛到一个有限圆．

1 预备知识

由于改变曲线流方程的切向分量仅影响曲线流的参数表示，我们选择合适的切向分量η来简化计算．考虑以下等效方程：

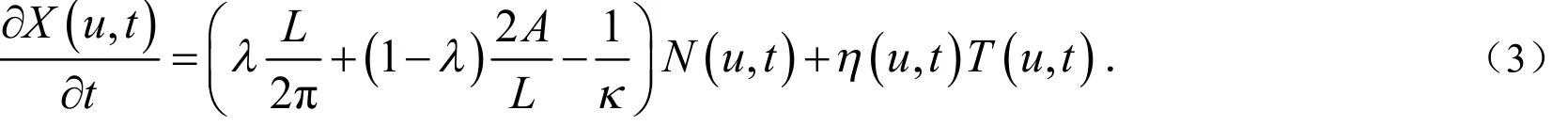
引入弧长参数 s = s （u, t），记 g （u,t） =是切向量的长度，弧长的微分可以写成 d s = g（u,t） du ．假设θ是x轴的正方向与切向分量T之间的角，在方程（3）下，发展曲线的几何量发展方程如下：

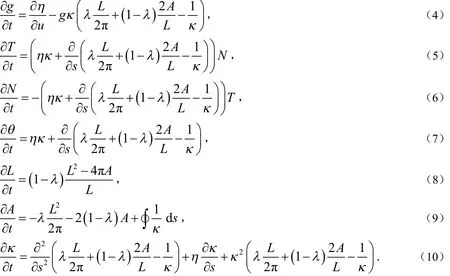
由此可以注意到曲线的长度L以及它所围成的面积A都是不依赖η的．通常来说，θ是关于u和t的函数．为了使θ只是关于u的函数，与时间t独立，即由（7）式可以得到：

为了简化计算，可以用参数（θ, τ ）代替参数（u,t）．曲率的发展方程可以写为：

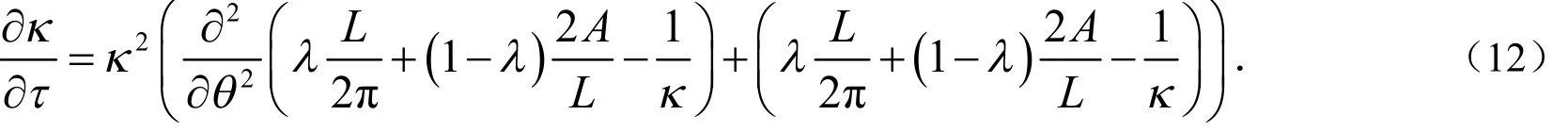
接下来将研究与方程（2）等价的曲线流的发展问题：

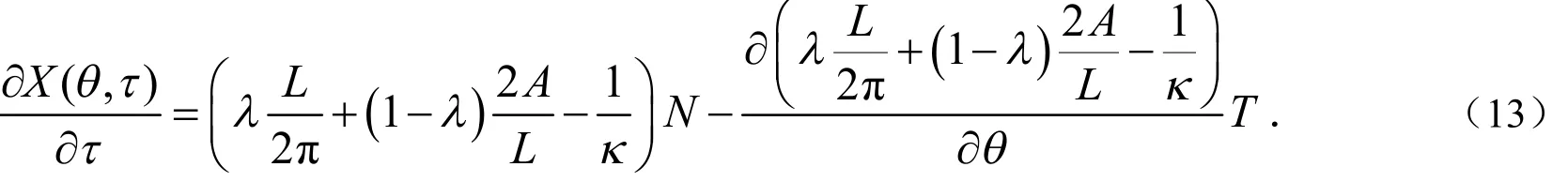
2 长度和面积都是增加的且有上界

这一部分将给出下面的证明．

定理2 曲线按照（2）式发展，在发展过程中，曲线的长度和它所围成的面积都是随着时间的增加而增大并且有上界．当t趋于无穷大的时候，等周差24πLA-随着时间的增大逐渐减少并收敛到0．

更重要的是，我们有：

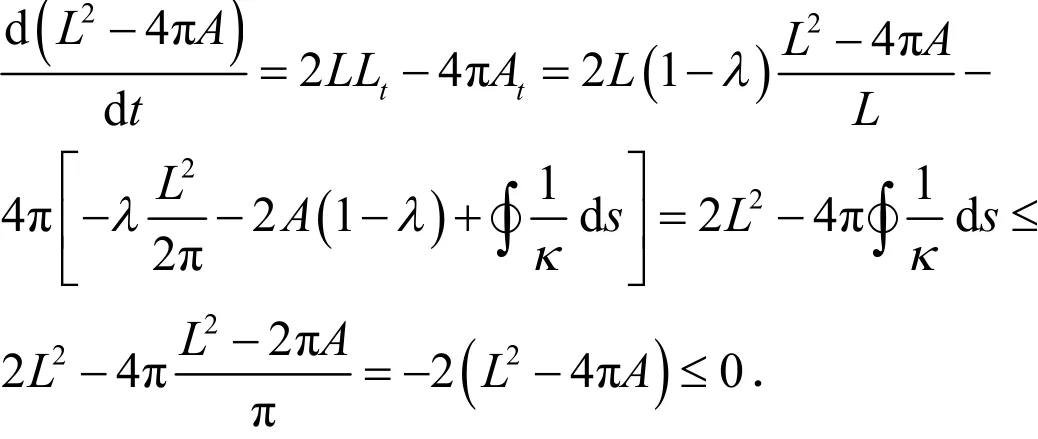
对上述不等式两边积分得：

结合经典的等周不等式，易知，当时间t趋于无穷大时，等周差24πLA-随着时间的增加而减少并收敛到0．

从方程（8）和（14）可以很容易地得到：

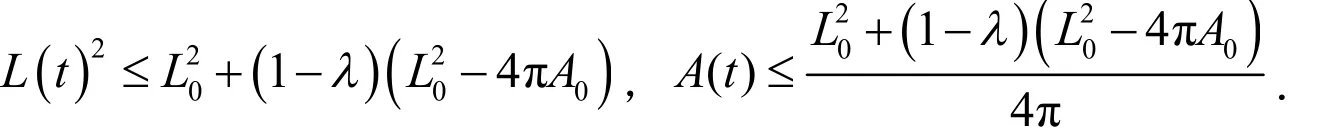
3 凸性和长时间存在性

这一部分将用与文献[8]同样的方法来证明曲线流（2）的凸性和长时间存在性．

引理1 曲线流（13）的曲率发展方程可以转化成标准热方程，它的解在任意时刻都存在．证明：由（12）式可以得到：

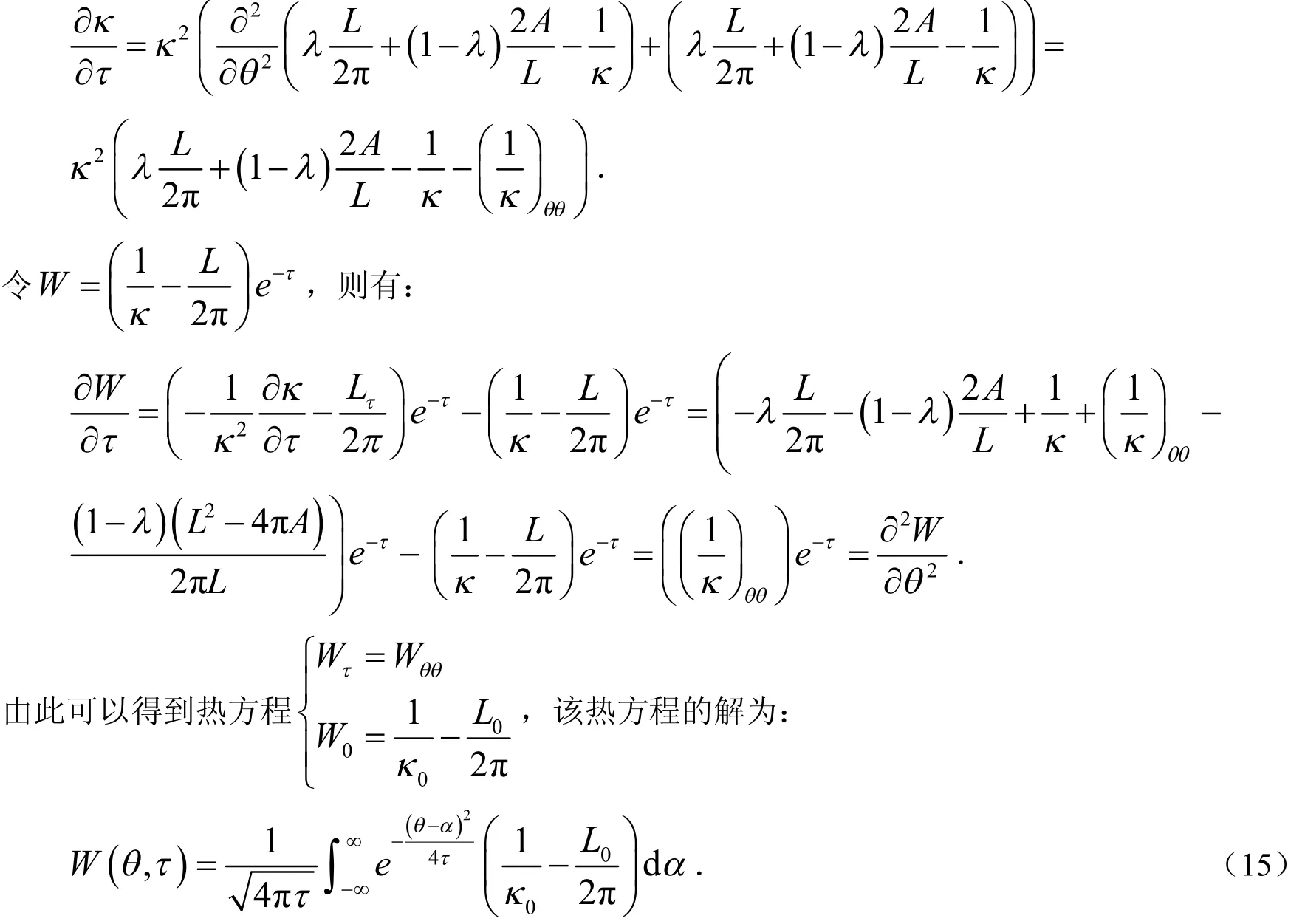
引理2 若一条封闭的凸曲线按照方程（13）发展，则曲线流在发展过程中始终保持是凸的．

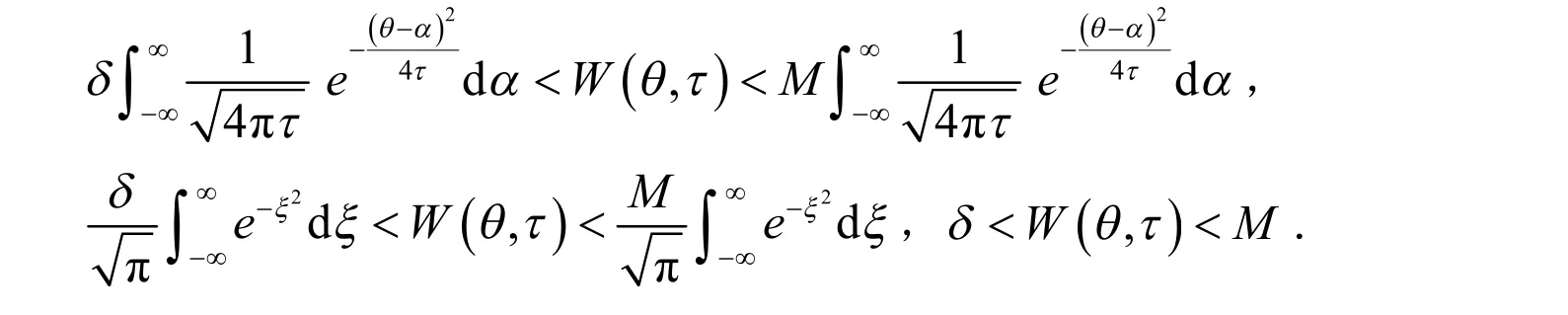
曲线流的支撑函数是光滑的并有全局存在性，下面将运用支撑函数的这种特性得到曲线流的长时间存在性．

引理3 支撑函数的发展方程如下：

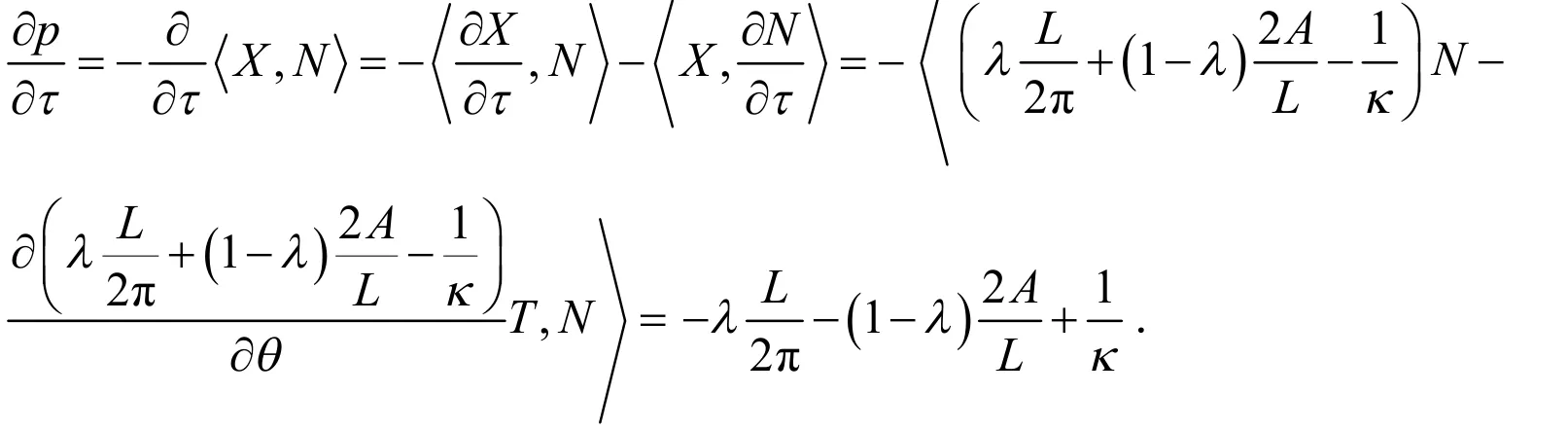
通过直接计算，就可证明该引理．

引理4 支撑函数p存在于区间（0,2π）×［0,∞），且满足

4 定理1的证明

如果曲线按照方程（2）发展，根据定理 2可知，曲线的长度和它所围的面积是随着时间的增加而增大的．通过引理2可知，曲线流在发展过程中保持凸性．从引理4和引理5可知支撑函数的全局存在性，因此曲线流的方程（13）与方程（2）等价．此外，由文献[16]中的 Bonnesen不等式即曲线在C∞范数下收敛到有限圆．