提高高中生数学运算能力的教学策略
江苏省海州高级中学 李旭萃
一、在课堂上加强对数学运算能力重要性的引导
高中生数学计算能力低下不仅仅体现在数学学科内,其他学科的许多教师也反映“数学没有学好,理化计算题一做就错”。因此,课堂上积极引导学生提高对数学运算能力重要性的认识是不可缺失的。如:通过法则迁移、合理选择公式运算、对函数关系进行变形和数据处理、在问题情境中分析条件和目标,探究出合理而简捷的运算流程等等,这是运算思维能力和运算技能相互融合的具体表现,也是教学实践过程中教师强化学生数学运算能力,进行数学建模的重要抓手。
二、在课堂上加强对数学概念和基础知识的准确理解
高中数学有着许多重要的数学概念、公式、法则和性质,很多知识是互通的,也有很多知识是很容易混淆的。如平行线和异面直线都是不相交直线,在计算两条直线的距离时,过一条直线上的任一点作另一直线的垂线,其垂线段是平行线间的距离,但不一定是异面直线间的距离,学生经常会将概念张冠李戴,出现计算失误。因此,在课堂上引导学生正确认知数学概念,在熟练掌握概念的基础上记忆、运用是重要环节,这样才能潜移默化地培养学生的数学运算能力。
三、在课堂上加强对数学运算的科学系统训练
数学运算的技能是通过训练提升的。在课堂上,学生需要训练什么、怎样去进行训练,都是授课教师必须掌控的。课堂训练必须具有科学系统性、合理有效性,是对学生学科素养的一种技能训练。
1.数学运算的训练必须是循序渐进的
数学运算不可能一蹴而就,需要漫长的积累过程。在这个过程中,需要教师准确定位,做好相应的训练计划和操作流程,循序渐进。如在学习《圆锥曲线与方程》时,首先采用例题示范教学:求与圆x2+y2=m2的圆周的距离为m的Q点的轨迹方程。接下来设计难度较低、略有变化的训练题,要求学生按图索骥,用规范的步骤和法则进行推导运算。如练习:求与圆x2+y2=n2的圆周的距离为m的R点的轨迹方程。
通过在例题教学中引入变式练习,让学生在示范模仿中强化训练,从而渐渐进行数学建模,然后再对数学运算的过程、依据、方法进行相同构建,以达成提高运算技巧之目的。
数学运算的训练必须是循序渐进的,前面的过程是为了夯实基础、巩固概念,而后一个环节,也是最重要的环节是综合训练,选择的练习题必须具有一定难度,以训练学生把握运算方向、体验运用法则的灵活度,完成数学建模,从而有效提升数学运算能力。
2.数学运算的训练必须是定时的
任何知识的学习都会产生“高原”现象,对学生的数学运算技能训练也不例外,经过一段时间训练后学生会出现停滞不前的现象。所以,需要根据学生的认知水平以及运算能力,确定数学运算训练的难度和时长。一方面要避免不必要的重复,另一方面是限时限量,稳扎稳打。这种训练是章节整合形式的,数学计算是穿插式的、交叉式的。如采取“5 选择+4 填空+2 大题”的形式,让形式多元化,限定时长60 分钟,既与高考形式接轨,又抑制了学生的厌倦情绪,使得训练有着明显的效果。
3.数学运算的训练必须是步步为营的
学习的过程是“温故而知新”的过程,是对旧知拓展延伸的过程。数学计算的训练过程更-需要及时反馈、评价、纠错,让学生学会查漏补缺。很多学校建议学生做“错题本”,这是一种步步为营的学习方法。数学计算的训练过程何尝不是如此。每一次训练都需要教师批改后的及时反馈,对学生的练习情况进行评价:鼓励、督促、错误分析,不但可以激发学生的学习动机,而且可以驱动学生的认知潜能。例如:
方 程x2-2kx+k+6=0 的 两 实 根 为a和b, 且k为 实 数, 则(a-1)2+(b-1)2的最小值是( )
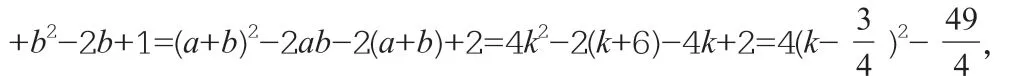
学生的失误在于没有认识到a、b是两个实数根,没有考虑方程的判别式有意义。经过课堂反馈和分析,学生茅塞顿开,今后做类似的习题时当然就会注意细节了。这类数学运算问题的案例数不胜数,翻开学生的做错题本比比皆是,就不再细说了。
总之,高中数学运算能力是学生的基本功,需要教师在课堂上正确引导,让学生真正重视起来;需要学生在课堂上对数学概念和基础知识的准确理解,夯实运算的过程基础;更需要师生在课堂上共同加强对数学运算的科学系统训练。只有这样,才能让学生建立数学概念的理解和运用在数学运算中的必要性,认知建立数学模型在数学运算中的重要性,才能提升学生的数学素养。

