脑磁图脑功能连接网络癫痫棘波识别方法研究

张航宇，李 彬，尹春丽，刘 凯，王玉平，张军鹏

1.四川大学 电气信息学院 自动化系，成都610065

2.首都医科大学 宣武医院 神经内科，北京100053

1 引言

癫痫是大脑神经元异常放电，导致大脑功能障碍的一种慢性脑部疾患，以脑部神经元过度放电所致的突然反复和短暂的中枢神经系统功能失常为特征[1]。在我国，癫痫的患病率约为3‰ 至6‰ ，难治性癫痫约占20%[1-2]，目前全世界患有癫痫疾病的人数约占总人口数的1%，且每年以0.02%～0.05%的速度增长[3]。

自发功能连接（spontaneous Functional Connectivity，sFC）已成为认知神经科学的一个主要工具[3]。自发功能连接是基于对脑区间的自发波动信号之间的统计关系的分析，一些研究提出它能反映脑区之间的深层神经互动[4]。作为神经科学研究的一个工具，自发功能连接能够帮助理解脱离任务环境下的大脑是如何工作的[5]。自发功能连接作为一个重要且广泛使用的工具，它可以检测典型大脑的功能连接并记录神经发育[6]，还可以描绘神经学和精神病学失调病症的异常脑活动的特性，这些病症包括中风、帕金森症、阿尔兹海默症、癫痫和自闭症。

自发波动由Biswal 基于功能磁共振数据在血液氧合中第一次观察到，随后同样的网络在大脑电生理学记录脑电图和脑磁图中也被观察到[7]。很多研究出于高空间分辨率的原因使用功能磁共振成像，但是它的低时间分辨率（0.5～2 Hz）和血管决定的对比度使它不能直接研究被认为是脑区间信息交流机制的高频神经皮层活动[8]。除此之外，神经活动的时间尺度是典型的远远快于fMRI的记录能力的[9]。

脑磁图（Magnetoencephalography，MEG）是一种非侵入式的测量神经集束树状活动所引发磁场的方法，它的采样率超过500 Hz，能够直接用来研究快速神经活动[10]。为了获取多样的神经生理学相关频段，本研究使用MEG，这是由于它的时间分辨率高。有些研究已经证明了使用皮层区域间相位关系作为功能连接量度的有效性。特别的，相位锁定值是衡量两个时间序列间相位同步性的方法，它以前被用于分析MEG 的静息态连接，来建立脑功能连接网络。脑磁图检查是辅助癫痫诊断的一个非常重要的手段。癫痫在脑磁图中的主要表现是棘波和尖波，有时对它们不作区分，统称为癫痫瞬变现象[11]或棘波。棘波和尖波突出于背景活动，波幅较高，周期为20～200 ms。

脑磁信号的分析主要是对大脑异常活动的检测分析，这些工作目前都是由医疗工作者根据经验通过对患者脑磁图的视觉检测完成的。视觉检测有许多不利的因素，一般一次检测要记录60 min 的数据，从很长的数据中找出棘波非常耗费精力，对分析者的判断力有很高要求，并且医生在工作中要接触大量癫痫病例，在繁重的工作任务下分类结果的准确性无法保证。而且，不同的专家对同一记录的判断结果也不尽相同。因此，对异常大脑电生理信号的自动检测就显得十分重要[12]。

不论选用何种检测标准，通常要求棘波检测结果有较高的正确率，较低的漏检率和误检率。本文提出一种基于Desikan-Killiany 脑区划分的相位锁定值脑功能连接网络全频段的机器学习棘波检测方法，可对大脑棘波放电状态进行客观的标定，有很大的潜力应用于脑磁图癫痫棘波的自动识别与标记的辅助工具，降低医生的劳动强度，提升检测正确率并降低漏检率和误检率。

2 数据与方法

2.1 数据采集

本文使用的MEG数据来自于首都医科大学宣武医院脑磁图中心做检查的20名被确诊为岛叶及岛盖癫痫的患者，均在手术前进行了MEG检查，其中男11例，女9例；年龄15～52岁，平均28.7岁。

MRI 应用1.5T 或3.0T 进行标准的MRI 扫描，包括横断位SE 序列T1W1 及TSE 序列T2W1（层厚5 mm）；垂直于右侧海马长轴的斜冠状位和平行于海马长轴的横断位液体衰减反转恢复（FLAIR）序列（层厚5 mm）。

MEG 应用芬兰Elekta Neuromag Oy 公司生产的NM20215A-G 型306 信道全头型生物磁仪对患者进行检测。患者于安静状态下于磁屏蔽室记录60 min自发脑磁图数据。带通滤波为0.10～330 Hz，采样率1 000 Hz。脑磁源成像（MSI）采用标准程序306导全头型脑磁图系统进行采集，对发作间期癫痫样波进行标记、离线分析。脑磁波与病人MRI 图像进行融合，在MRI 上自动生成MSI图像。

脑磁图中心的医生根据经验为每位病例挑选出三段含棘波的数据区段，每段各10 s，并标出棘波峰值的时间点；作为对比同时提供每位病例三段正常静息态的数据区段，每段各10 s，为了保证本次选出的棘波数据与正常静息态数据的正确性与典型性，特意请不同的医生进行了交叉检查确认，确保了本次研究采用的两种数据均为典型棘波态与典型正常静息态的脑磁图数据。

2.2 数据预处理

获取了医生用传统方法挑选出的全部20例病例的MEG数据后，采用基于数学软件矩阵实验室（MATLAB）平台下的MEG 分析软件Brainstorm（brain recordings analysis tool）进行数据预处理。首先，对MEG 进行滤波得到0.1～500 Hz频段数据；然后，去除数据中的伪迹，主要包括眼电、眼动等对MEG的干扰。

所有数据均严格按照上述方法依次进行处理后，从医生提供的10 s 有棘波数据段中截取含棘波峰值的数据段2 000 ms，从10 s无棘波数据段中间截取相同长度的数据段；最后共获得2 000 ms时长的有棘波数据段与无棘波数据段各60段，这些数据是进一步分析的基础。

2.3 脑功能网络建立

所有数据均通过基于Uhuntu 平台的工作站，调用FreeSurfer 软件包，进行自动化分析处理。分析处理过程分为体积处理流程与表面处理流程两大部分。体积处理流程包括图像灰度标准化、不均匀磁场的校正、到Talairaeh 空间的配准、非脑组织的去除和白质（White Matter，WM）与灰质（Grey Matter，GM）的分割等。表面处理流程包括对白质曲面进行三维重建，从白质曲面出发，沿着灰质梯度方向向外膨胀得到灰质外表面曲面。定义灰质曲面和白质曲面间的距离为脑皮层厚度，采用T-average算法计算皮层厚度。灰质外表面向外膨胀，得膨胀曲面。膨胀曲面经过球状形变后与模板进行高维配准，依据Desikan-Killiany图谱对皮层进行自动分区。Desikan-Killiany 图谱将全脑分为70 个脑区（左右半脑各35 个），其中胼胝体没有灰质厚度，因此最后得到68个脑区（左右半脑各34个）的皮层厚度。对全部数据用Brainstorm软件中自带的Dipole方法进行求源处理，接着对每位病例每个波段求源过的数据按照Desikan-Killiany图谱进行下采样。

脑网络最基本和最关键的两个组成元素是节点和边：节点代表了大脑的各个脑区，边则能反映各个脑区之间的联系。Desikan-Killiany模板所划分的68个脑区被定义为脑网络中的节点，如图1 所示，每个脑区是一个节点。

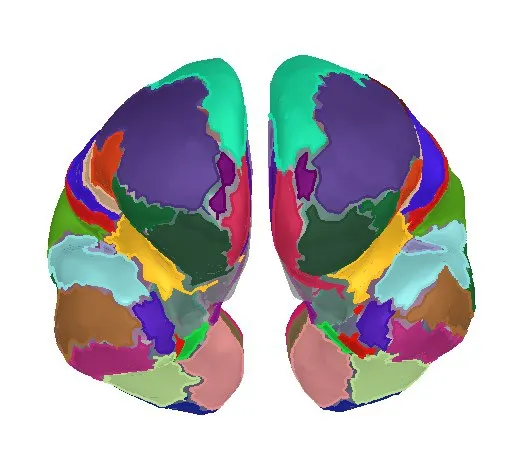
图1 全脑68个脑区分区图

脑功能网络使用相位锁定值（Phase Locking Value，PLV）[13-14]构建。相位锁定值是对两个时间序列信号在一段时间内保持恒定相位分离的倾向的度量。对于电生理学记录的时间序列之间静息态相位锁定的测量，可以表征在给定频率下这些时间序列之间的相位差随时间变化的特性。PLV的计算公式如下：

其中，N 是采样点的个数，θ1和θ2是采样点n 处的瞬时相位值，相位锁定值为复数，其模的范围为0到1，0代表随机的相位关系，1代表固定的相位关系。相位锁定是一种无方向的量度方式，因此是对称的。全脑相位锁定网络是在每一对皮层脑区时间序列测量结果之间计算出来的，由于相位锁定的对称性，只需要在每一对时间序列测量结果之间计算一个相位锁定值。

下采样之后得到每个源的数据，之后对频率范围为0.1～500 Hz的全部两组数据中的所有个体数据段分7个频段分别求出相位锁定值（PLV）矩阵。全部7个频段从F1低频到F7高频的对应频率范围如表1所示。

表1 频段对应表

为了有代表性，随机选取单一频段下相位锁定值矩阵作为典型展示，在此选取3号病例alpha频段下2 000 ms时长数据段的相位锁定值矩阵展示于图2中。

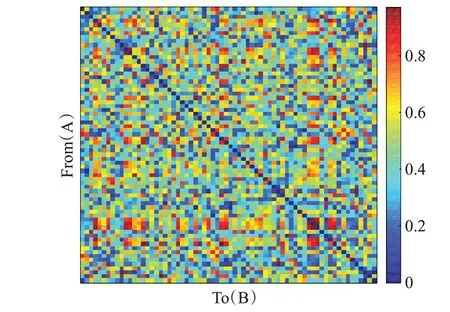
图2 相位锁定值矩阵

3 模型设计

本文使用了三种传统的分类算法，分别是线性逻辑回归分类、基于线性核函数和径向基核函数的支持向量机分类与高斯朴素贝叶斯分类算法。以上模型均使用了scikit-learn框架下的函数实现。

3.1 线性分类原理

本文使用Sigmoid函数作为线性逻辑回归（Logistic-Regression）分类器函数。Sigmoid函数是使用范围最广的一类分类函数，该函数定义为：

其中，y 是样本被判别为正例的概率，1-y 为样本被判别为负例的概率。为保证模型的训练精度，损失函数引入L1正则化项，其中设定正则化系数倒数C=1.0，模型预测值为二分类的概率值，其损失函数为：

计算损失函数取最小值时的参数(w,b)，即能得到最优的分类模型。

3.2 支持向量机分类原理

支持向量机在高维度或无穷维度空间中，构建一个超平面或者一系列的超平面，借助超平面去实现分割，使正负样本之间的空白最大。该模型对非线性关系分类有较好的效果。基本原理如下。

给定训练向量xi∈RP,i=1,2,…,n 和一个标签向量y ∈{1,-1}n。在样本空间存在一个超平面wTx+b=0 可以实现对样本进行有效分类，则有：

使得式（4）等号成立的距离超平面最近的几个点构成支持向量，正反方向支持向量到超平面的距离之和为使得该距离最小的参数即为最优参数。用作为式目标函数，按照拉格朗日乘子法进行优化，简化为对偶问题：

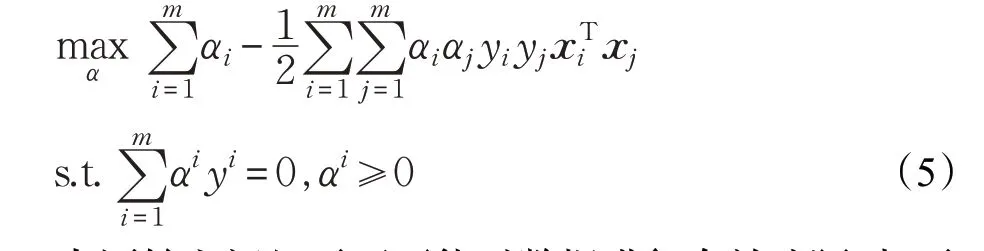
当原始空间超平面不能对数据进行有效分隔时，需要将数据映射到高维空间，即。在对偶问题中，寻找核函数使得，以便在较低维度空间实现内积计算。本文采用线性核函数（kernel：linear）和径向基核函数（kernel：rbf）。

3.3 朴素贝叶斯分类

朴素贝叶斯分类（Naive Bayesian Classifier，NBC）由于计算高效、精确度高，并具有坚实的理论基础而得到广泛的应用。一般情况下在贝叶斯分类中的所有属性都直接或间接地发挥作用，即所有的属性都参与分类，而不是一个或几个属性决定分类[15]。贝叶斯分类器的分类原理是通过某标签的先验概率，利用贝叶斯公式计算出其后验概率，选择具有最大后验概率的类作为该对象所属的类。简单地假设任意两对特征之间相互独立，假设每个样本为独立同分布，根据中心极限定理，标准化之后的每个特征的数据满足高斯分布的假设，即P(xi|y)～Gaussian，根据贝叶斯定理，则有：

根据每对特征之间相互独立的假设，从而有：

根据式（7）即可计算y 的后验分布。

3.4 原始特征构建

在研究中，先使用作为原始特征空间的PLV复数矩阵数据本身（plv）、该矩阵数据的实部（plv_real）、虚部（plv_imag）、幅角（plv_angle）和模（plv_abs）分别进行了测试。结果表明，在使用的所有模型中，模数据表现最为优异。以朴素贝叶斯分类器模型为例，采用五项数据分类的准确率如表2所示。

表2 基于朴素贝叶斯分类器模型的准确率分布表

经测试，在本文使用的其他四种分类器模型中以上五种数据均有类似表现，因此本文所提到的数据均为PLV复数矩阵的模（plv_abs）数据，选定该原始特征空间复数矩阵的模数据作为原始特征数据集。

在实验中使用以上四种分类器对plv_abs数据分别进行学习分类，实验结果如表3所示。

表3 基于原始数据的不同模型分类准确率和AUC结果比较

4 实验结果与分析

4.1 实验流程

首先根据120×15 946的原始特征数据集作为输入，然后对输入数据集做了标准化，最后对标准化后的数据集应用卡方检验、F检验与迭代特征消除三种方法进行了特征提取；应用四种分类器分别对上述数据进行分类实验，对全部实验结果进行了分析与比较。原始特征数据集构建之后的处理流程如图3所示。

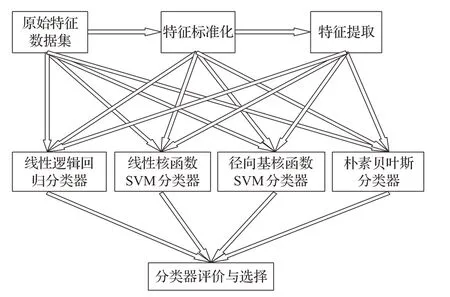
图3 实验流程图

4.2 实验结果

为定性地比较各种不同的方法，本文对比了四种分类器的受试者工作特征曲线（Receiver Operating Characteristic Curve，ROC）图。ROC 曲线是反映真阳性和假阳性的综合指标。本文的四种分类器对结果的预测均为一个概率值，其中有棘波的标注为正例，正常无棘波状态标注为负例。按照判别为正例的概率值对测试结果进行排序，再以不同概率值作为正反例判别的阈值，并计算相应阈值下的真阳性率和假阳性率，即可绘制得到分类器的ROC曲线。一般根据对分类任务的不同要求，根据曲线对分类器性能的评判存在不同的标准，且本文的分类器ROC曲线存在交叉，因此本文按照通用的AUC（Area Under the ROC Curve）方式对分类器性能进行评价。AUC是ROC曲线与轴所包络部分的面积，面积越大，表明该分类器的分类性能越好。

4.2.1 原始特征数据集的实验比较

使用plv_abs 数据作为原始特征数据集输入，在对四种个分类模型进行训练后，实验结果如表3与图4所示。

图4 原始数据的ROC图

从表3与图4中可以看出使用朴素贝叶斯分类器模型准确率为0.875，比其他三种模型都要高，其AUC 值为0.914，也是所有分类器中第二高的，说明对原始数据而言使用线性核函数的支持向量机分类器性能最好。

4.2.2 特征标准化的实验比较

对原始特征数据集的各列特征向量数据均按照公式（8）进行了标准化处理：

其中，xi表示第i 个特征向量，σi表示该列特征的标准差，μi表示第i 个特征的均值，xstd表示标准化之后的特征向量。

使用标准化后数据作为输入，在对四种模型进行训练后，测试结果见表4和图5。

在对原始训练集的各列数据进行标准化处理后，线性逻辑回归分类器的准确率从0.771提升为0.917，使用线性核函数的支持向量机分类器的准确率从0.833提升为0.917，而径向基核函数支持向量机分类器的准确率从0.500 提升为0.938，说明提升最高，朴素贝叶斯分类器的准确率也从0.875小幅提升为0.896，说明对原始训练集的各列数据进行标准化处理有利于提升准确率，并且四种分类器就准确率而言性能相差不大，结合作为分类器性能评价标准的AUC 值，径向基核函数支持向量机分类器的AUC 值为0.951，在四种分类器中值最大，故综合上述结果，使用标准化后的特征数据集作为输入，选用径向基核函数支持向量机分类器进行棘波自动分类的效果最好，成功率为93.8%。

表4 基于标准化数据的不同模型分类准确率和AUC结果比较

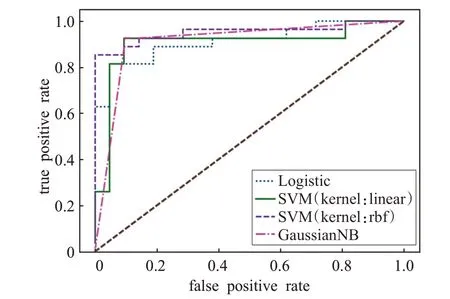
图5 原始数据标准化的ROC图

4.2.3 特征提取

在现实的人类识别中，根据经验知识能够轻易识别棘波的存在及相关影响，很明显未能短时间速实现对15 946 维数据的观测和判断，因此推断，数据的维度中必然存在大量的冗余，因此在适当容忍模型性能降低的基础上进行了特征选择，以降低模型的复杂度。

（1）基于单变量的特征选择

基于单变量的统计测试，通过过滤的方式选择特征。本文采用卡方检验和F检验方法，逐一对单个特征与实验标签进行相关性检验，并根据相关性排序选择部分特征。基于对提取后的特征多次测试，判定选择32个特征，即整体特征数的0.2%时就能达到较高的分类准确率又能大幅度降低特征数量。F 检验和卡方检验所提取的32个特征并不一致。

（2）基于模型的循环特征消除（RFE）

本文采用Logistic回归分类模型，并使用了L1进行正则化，选择了32个特征。

4.2.4 特征选择后数据的实验比较

分别使用3 种特征选择方法筛选后的32 个特征向量作为输入，在对4 种分类模型进行训练后，实验结果如表5和图6～8所示。

表5 不同特征选择方式下分类器准确率比较

图6 基于卡方检验提取特征的学习分类ROC比较

图7 基于F检验提取特征的学习分类ROC比较

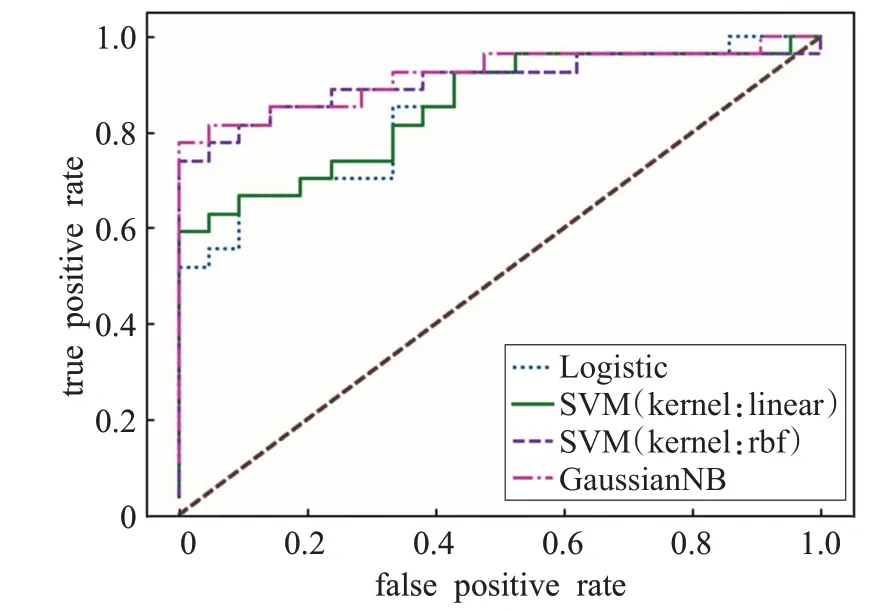
图8 基于迭代特征消除后特征的学习分类ROC比较

从表5 与表6 中可以看出，经过迭代特征消除方法进行特征选择后，在四种分类器下的分类准确率与分类器的AUC 值均低于其余两种选择方法，说明此种特征选择方法的效果不好，故重点关注卡方检验和F检验特征提取选择方法。

与特征标准化后的实验结果比较，线性逻辑回归分类器的准确率从0.917 降低为0.833 与0.833，线性核函数支持向量机分类器的准确率从0.917 降低为0.896 与0.792，而径向基核函数支持向量机分类器的准确率从0.938降低为0.833与0.854，说明经过特征选择后，使用上述三种分类器分类，准确率会有所降低，而对于朴素贝叶斯分类器，使用卡方检验和F检验特征提取后的数据作为输入，其准确率从0.896 提升为0.917，分类器AUC 值从0.912 提升到0.951，比其余三种分类器均要高，说明针对卡方检验和F 检验特征提取，朴素贝叶斯分类器性能最优，分类效果最好。

表6 不同特征选择方式下各模型的AUC比较

5 结果讨论

5.1 模型选择

在本文的研究中，通过医生的精心挑选得到正常静息态与棘波态脑磁图样本数据，数据被适当地预处理后，分七个频段经相位同步的PLV算法计算，得到68个脑区之间的PLV复数值矩阵作为特征空间，取该特征空间的模值数据作为原始特征数据集，然后对原始特征数据集做了标准化，最后对标准化后的数据集应用卡方检验、F 检验与迭代特征消除三种方法进行特征提取，最终构成了五种用于输入分类器的数据集；本研究中，应用了机器学习的方法，包括线性逻辑回归、线性核函数支持向量机、径向基核函数支持向量机与朴素贝叶斯分类算法，构建了四种对应的分类器，将五种输入数据集依次使用四种分类器进行分类实验，得到相应的分类准确率，对分类器本身使用绘制受试者工作特征曲线（ROC）图并计算对应的AUC值方式对分类器性能进行评价，最终得到，在应用标准化后特征数据集不进行特征选择提取时，径向基核函数支持向量机分类器的准确率最高，为93.8%，AUC 值为0.951 所以性能最优；应用卡方检验、F 检验进行特征提取后的特征数量大为减少，对应此种精简特征数据集时，朴素贝叶斯分类器的准确率虽与完整特征数据集下最高分类准确率相比稍有降低，也可达到91.7%，AUC值为0.951，故性能与完整特征数据集下的径向基核函数支持向量机分类器相当。

5.2 基于特征选择的脑区识别

根据特征选择的结果，32个特征基本能够实现对数据的较好分类。但基于F 检验和卡方检验提取的特征存在较大不同。按照68×68 矩形区域的上三角部逐行编号，两类检验的提取结果如表7。

从表7 可以得到，卡方检验和F 检验提取特征的分布上存在18个重叠特征，因此可以断定，这18个特征对判别是否是癫痫症患者具有重要影响。

表7 卡方检验和F检验提取特征编号的分布

6 结论和建议

对本文列出的18 个关键特征位置还原计算，得到所处的位置分别为：（1，20）（1，22）（1，60）（9，13）（12，20）（15，31）（15，65）（18，33）（18，48）（18，52）（25，42）（28，38）（30，61）（30，62）（31，38）（32，54）（55，66）（59，65），18个特征全部处于delta频段。因此，可以断定，决定癫痫的脑电信号可以完全由delta频段的信号完成判别。建议在后续医疗实践中，对以上18 个特征所对应的18 对大脑皮层区域之间的信号传递加以重点关注，下一步从临床实践上对以上脑区开展研究。