基于特征模型的主动磁轴承交叉反馈控制研究

江绪鑫，徐龙祥

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

理论上，在磁悬浮产品的设计中传统工业所采用的分散PID控制能够保持磁悬浮转子的基本稳定，而在实际应用中，由于转子转速的提高，陀螺力矩的不断加强仍然会对系统的动态性能产生不利影响[1-2]。常用的抑制陀螺效应的方法有两种，一是采用交叉反馈控制技术，二是采用鲁棒控制技术。交叉反馈控制通常是在传统分散PID控制的基础上加入交叉反馈环节[3]，以达到抑制陀螺效应的目的。为了进一步延伸交叉反馈控制的应用领域，本文提出了基于特征模型的磁悬浮轴承交叉反馈控制。从部分工业控制对象的物理机理、动力学特性和环境特征出发，结合控制目标与性能要求，建立其对象的特征模型。

1 磁悬浮轴承的数学模型

图1为四自由度转子试验台的刚性支撑力学模型，其中起径向支撑作用的是分布在左、右两端的径向磁悬浮轴承a和径向磁悬浮轴承b。当铁芯转子处在起浮或旋转过程中时，由传感器a和传感器b检测a、b两端转子轴心处的位移，并反馈给以DSP28335为核心的主控制器[4]，随后控制器根据位移量的变化输出对应的电压控制率，再由功率放大器依据控制率的变化改变两端磁悬浮轴承的线圈电流大小，进而改变轴承的控制力Fx、Fy。

图1 转子试验台的刚性力学模型

根据图1可列出磁悬浮转子径向四自由度的动力学方程如式(1)所示。为了避免传感器安装位置差别带来的误差，通过一系列位移矩阵变换，得到了由传感器处输出的位移、位微分、控制电流向量所组成的转子系统状态空间方程式(2)。

(1)

(2)

2 基于特征模型的交叉反馈控制理论

2.1 特征模型及辨识方法

所谓特征模型就是根据对象的动力学特性、控制性能要求和环境特性相结合来建模[5]。对于高阶复杂对象，为了满足控制性能要求，特征模型可以将系统的高阶分量压入4个慢时变的系数中，从而简化被控对象，利于低阶控制器的设计。一般的高阶线性定常系统表示为：

在满足一定采样周期Δt时，线性定常n阶对象G(s)可以表达为：y(k+1)=f1(k)y(k)+f2(k)y(k-1)+g0(k)u(k)+g1(k)u(k-1)。

特征参量f1(k)、f2(k)、g0(k)、g1(k)均有慢时变性质，在动态过程中，同等的输入情况下，特征模型的输出与实际对象的输出等价；当静态增益D=1时，在稳态情况下系数之和=1，即有：f1(k)+f2(k)+g0(k)+g1(k)=1。

系统特征参量的辨识通常有两种方法，一是最小二乘递推参数估计方法，二是类似于随机逼近的梯度下降法。由于最小二乘递推算法包含复杂的矩阵运算，计算量过大不利于控制器实现，本文采用梯度下降法。梯度下降法的估计表达式为：

(3)

2.2 基于特征模型的交叉反馈控制

基于特征模型的交叉反馈控制的主控制算法为特征模型算法，而特征模型算法只是辨识出了系统的特征参量，实际输出控制率是以全系数自适应算法为载体而进行输出的，全系数自适应的控制量u(k)总共包含了4个部分的控制量：微分控制量ud(k)、积分控制量uI(k)、维持给定控制量u0(k)、黄金分割比控制量ug(k)，4个控制量的表达式分别如下：

1) 微分控制量

与PID控制器相同，微分控制量ud(k)的参入是为了改善系统的动态性能，其描述为：

ud(k)=kd(e(k)-e(k-1))

(4)

2) 积分控制量

uI(k)=uI(k-1)+kI(yr(k)-y(k))

(5)

同样与PID类似，积分控制量uI(k)的作用是消除系统稳态误差。

3) 维持给定控制量

维持系统稳定的标准就是为了使系统的输出位移y(k)能够与要求的恒定值yr(k)相同，设计系统的维持给定控制量u0(k)为：

(6)

4) 黄金分割比控制量

对于被控对象数学模型不精确的情况，在系统启动阶段，可以采用黄金分割比控制来维持系统的稳定。可以取黄金分割比控制器的控制率为：

(7)

为了将基于特征模型的全系数自适应算法与PID算法联系起来，将维持给定控制量与黄金分割比控制量相加得到下式：

(8)

式中ε是一个慢时变微量，其值是一个范围在0～1之间满时变变化的正数与给定位移值的乘积。

可将维持给定控制量u0(k)、黄金分割比控制量ug(k)、微分控制量ud(k)写为以下形式：

ug+0(k)+ud(k)=P(k)+D(k)

(9)

那么可以将特征模型算法的控制量写为以下形式：

u(k)=P(k)+D(k)+uI(k)

(10)

式中P(k)、D(k)可以看做具有慢时变性质的比例、微分系数。借此可得基于特征模型的交叉反馈控制下的电磁力[6]的输出表达式：

带入式(1)可得：

求得交叉反馈系数表达式为：

(11)

Ahrens指出在实际工程应用中，由于系统相位滞后等原因，完全补偿难以实现，令kvc=CeffJzω/kxi(la+lb)2作为补偿后的交叉反馈系数。

3 仿真分析

首先将系统的特征辨识模块(RLS)与全系数自适应模块(ACAC)组成一个特征模型算法综合模块[7](ACAC+RLS)，结合式(2)的系统状态空间方程以及交叉反馈控制理论原理在Matlab/Simulink仿真软件中搭建了基于特征模型的交叉反馈控制(ACAC+CFC)系统仿真平台，其具体结构如图2所示。

图2 基于特征模型的交叉反馈仿真模型

分别取的衰减因子Ceff为1、0.75、0.5、0，得到不同的转子左右平面运动轨迹图如图3-图6所示。

由图3-图6可知，当衰减因子为1，即完全补偿的时候，转子左右平面的摆振幅度也十分明显，而当不加入交叉反馈项即衰减因子为0时，转子的热套部分在摆动过程中就碰到了保护轴承，说明其摆振幅度较大难以稳定，控制效果较差，同样的现象还可以在衰减因子为0.5时看到。当衰减因子为0.75时控制效果最好，此时转子的摆振幅度较小。由于现实存在的各种干扰误差，并不能确定最佳的补偿量，还需要进一步在实验中观察转子的控制效果。

图3 Ceff为1时转子接近临界转速的左右平面轨迹图

图4 Ceff为0.75时转子接近临界转速的左右平面轨迹图

图5 Ceff为0.5时转子接近临界转速的左右平面轨迹图

图6 Ceff为0时转子接近临界转速的左右平面轨迹图

4 实验分析

为了验证基于特征模型的交叉反馈控制效果，分别在衰减因子为1、0.75、0.5、0时做了转子转速上升到470Hz旋转实验，接近一阶弯曲临界转速。转子在中心位置时的位移信号是2.5V，保护间隙为0.125mm，故1V代表50μm，轴心轨迹如图7-图10所示。

图7 Ceff=1时转子临界转速附近轴心轨迹

图8 Ceff=0.75时转子临界转速附近轴心轨迹

图9 Ceff=0.5时转子临界转速附近轴心轨迹

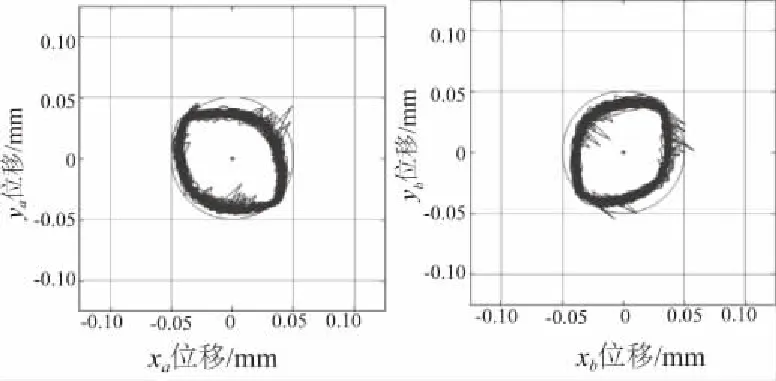
图10 Ceff=0时转子临界转速附近轴心轨迹

从实验的结果来看，当衰减因子为0.5时控制效果最佳，故以衰减因子为0.5时的交叉反馈系数实验数据，做出不含交叉反馈项的ACAC控制与衰减因子为0.5的ACAC+CFC控制的磁悬浮转子0～470Hz的振动位移峰峰值如图11所示。

图11 径向自由度转子各转速的位移峰峰值

5 结语

转子在ACAC控制下一到四自由度的振动位移峰峰值分别为0.114、0.083、0.085、0.107，而在ACAC+CFC控制下的振动位移峰峰值分别为0.093、0.066、0.076、0.095，径向各自由度的振动幅度分别减少了约18.4%、20.5%、10.5%、11.3%，此外ACAC+CFC在低频刚性模态频率中也同样有着较好的控制效果。