基于磁热耦合仿真的筒式永磁调速器散热研究

郭兰中，姚腾，李新勇，彭刘阳

(1. 常熟理工学院 机械工程学院，江苏 常熟 215000； 2. 中国矿业大学 机电工程学院，江苏 徐州 221000)

0 引言

永磁调速技术是一种调速节能新技术，相比于液力耦合和变频调速，永磁调速器具有软启动、不产生谐波污染等显著优点，成为风机、水泵等离心式负载节能改造的首选[1-2]。

方军、THOMAS、ALDO Canova等人对永磁调速器结构和材料性能参数对输出转矩的影响进行了仿真研究[3-5]；任庆等人利用二维有限元模型对涡流场和温度场进行了仿真分析[6]；徐伟、王旭等人利用三维瞬态模型对涡流场进行了仿真分析[7-8]。

国内外对永磁调速器的研究很少涉及散热方面，本文利用磁热耦合有限元模型对永磁调速器关键零部件的温度场进行了仿真分析，并对其散热结构进行了优化仿真分析。

1 结构与致热原理

1—散热片；2—铜环基体；3—铜环；4—气隙；5—永磁块；6—永磁块轭铁。图1 筒式永磁调速器结构图

筒式永磁调速器结构如图1所示。散热片、铜环基体、铜环组成导磁转子，固定连接到电机上，永磁块、永磁块轭铁组成永磁转子，固定连接到负载轴上。

工作时，电机带动导磁转子同速旋转，铜环不断切割永磁体产生永磁场，由于电磁感应现象，会在铜环中持续产生涡电流。当导磁转子和永磁转子之间的转速差增大时，铜环切割磁感线的频率加快，涡电流变大；当两转子啮合面积增大时，铜环切割磁感线的数量增多，涡电流也会变大。

感应产生的涡电流使铜环中产生大量热量，温度不断升高。这些热量还通过热传导、热对流方式向永磁调速器永磁体等部位传递，使其温度不断升高。当永磁体温度超过其临界工作温度时，其磁性能会明显下降。

本文对筒式永磁调速器两转子完全啮合、转差600r/min这一发热量较高的运行工况进行研究。通过磁热耦合仿真对其涡流场、温度场进行分析，并通过对散热片结构参量进行优化仿真，使永磁体温度降到其临界工作温度以下。

2 磁场研究

永磁调速器铜环中的热量是由磁场感应生成的涡流所产生，所以，要对永磁调速器铜环中热源的发热量和分布情况进行研究，就必须对产生涡流的磁场进行研究。

2.1 磁场仿真理论基础

对磁场的有限元分析都是基于Maxwell方程组，本文研究低频磁场，可忽略电流的位移效应，Maxwell方程组可表示为[9]：

(1)

式中：H为磁场强度(A/m)；J为涡电流密度(A/m2)；E为电场强度(V/m)；B为磁感应强度(T)。

铜环中的总电流密度可表示为：

J=Je+Jv

(2)

(3)

Jv=σv×B

(4)

式中：Je为变化磁场产生的电流密度；Jv为速度电流密度矢量；σ为电导率(S/m)；v为运动铜环速度(m/s)；A为矢量磁势；t为时间(s)。

根据式(1)-式(4)，可求出电流密度J和磁感应强度B。

2.2 磁场有限元仿真

1) 前处理

磁场建模时，模型各部件尺寸如表1所示，其散热片数量为40个。

表1 磁场、温度场仿真模型各部件尺寸 单位：mm

各部件材料属性如表2所示。

表2 磁场仿真各部件材料属性

Maxwell磁场仿真采用自适应网格剖分技术，并对铜环、永磁体进行网格加密处理。

求解采用瞬态方法，设置总求解时长为0.09s，分为30个时间步，每步求解时长为0.003s。

2) 磁场仿真结果分析

从图2可以看出，电流呈现涡旋状，且相邻两个涡电流矢量在相邻处叠加，使相邻处的涡电流值相对于涡旋中心处较高。涡电流的最大值达到7.08×107A/m2，这些涡电流产生的热量即为温度场分析的直接热量来源。

图2 铜环中电流密度幅值和矢量分布云图

3 磁热耦合研究

本文研究的永磁调速器永磁体采用N45H钕铁硼材料，其最高工作温度为120℃，在此工作温度以下，其磁性能相对稳定，所以本文采用磁热单向耦合的方法。

3.1 温度场理论基础

永磁调速器中铜环是直接发热源，其产生的热量通过热传导向铜环基体和散热片等部件传递，热传导的基本方程为：

Q=λAΔt

(5)

式中：Q为传导的总热量(J)；λ为导热系数(J/(m2·℃))；A为接触面积(m2)；Δt为温差(℃)。

热传导微分方程形式为：

(6)

散热片外表面、永磁转子内表面和各部件端面在运转过程中搅动周围空气，与空气进行强制对流作用，将热量散发出去，对流换热的基本方程为：

Q1=h(Tw-Tf)

(7)

式中：Q1为对流交换的总热量(J)；h为对流换热系数(J/℃)；Tw为散热片表面温度(℃)；Tf为周围空气温度(℃)。

其微分方程形式为：

(8)

式中：λx、λy、λz分别为求解域内x、y、z3个方向的导热系数；T为求解域内各点温度(℃)；qv为发热源的热流密度(W/m2)。

散热片外表面或永磁转子内表面对流散热系数可用下式求得：

(9)

式中：v为导磁转子外圆周面或永磁转子内圆周面线速度(m/s)；R为导磁转子外径或永磁转子内径(m)；n为导磁转子或永磁转子转速(r/min)。

导磁转子端面散热系数为：

(10)

永磁转子端面散热系数为：

(11)

式(10)-式(11)中：Re1、Re2分别为导磁转子和永磁转子端部气流雷诺数；n1、n2分别为两转子转速(r/min)；Nu1、Nu2分别为两转子端部努塞尔特常数；λa为空气的导热系数(W/(m·K))[10]；μ为空气运动黏度系数(m2/s)。

3.2 磁热耦合有限元仿真

1) 前处理

本文利用ANSYS Maxwell 3D模块和Steady-state Thermal模块进行耦合仿真，在Workbench中建立的关系图如图3所示，即将磁场仿真结果文件中的热生成导入到温度场分析的初始化设置中。

图3 磁热耦合仿真连接关系图

温度场分析的三维模型和磁场大致相同，需再建立一个两转子之间的气隙区域。散热片采用Workbench自带的模块DM进行重新建模，便于对散热片的底板厚度、肋片厚度、肋片高度、肋片数量这几个参量进行参数化设置。

使用控制变量法，设置散热片底板厚度h1在1.7mm～2.2mm变化，肋片高度h2在5mm～11mm变化，肋片厚度h3在1.4mm～2.6mm变化，肋片数量在37～42范围内变化，并对铜环温度、永磁体温度两个参量进行输出参数化设置。

温度场仿真中各部件材料属性如表3所示，其中两转子之间的空气区域流动状态较为稳定，可将其热量传递方式等效为热传导，直接赋予空气的导热系数值。

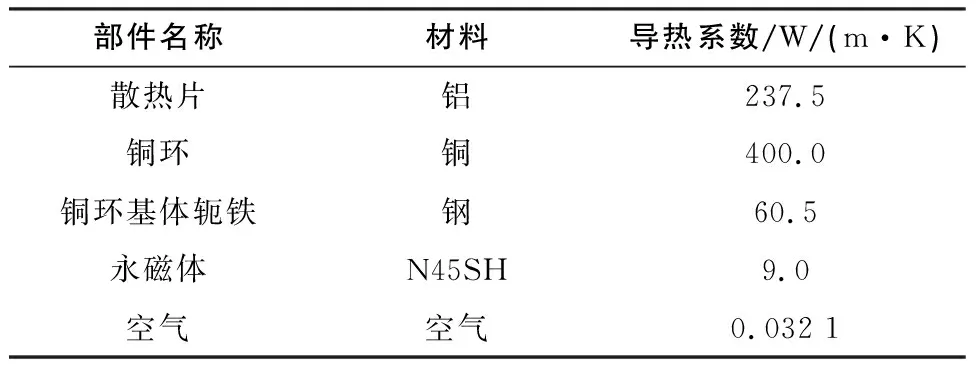
表3 温度场仿真各部件材料属性

温度场仿真中，筒体部件采用面网格进行剖分，其他部件指定最大单元尺寸进行剖分。

温度场仿真中分别对散热片外表面、永磁转子内表面以及两转子端面施加热对流载荷，其对流散热系数值按照式(9)-式(11)进行计算，并设置环境温度为22℃。

磁场仿真计算得到的涡流热以热生成率(W/m3)的形式施加到温度场仿真模型铜环部件中，其热生成率云图如图4所示，在轴向上呈现中间高、两端低的趋势，且铜环内表面的热生成率高于外表面。

图4 铜环热生成率云图

前处理设置完成，就可以开始求解，求解完成即可通过后处理得到铜环和永磁体上的温度分布情况以及散热片采用不同结构参数组合情况下的铜环和永磁体的最高温度。

2) 仿真结果分析

从铜环和永磁体温度分布云图(图5)可以看出，当永磁调速器温度达到稳定状态时，铜环上的温度呈现中间高两端低的趋势，且内表面温度略大于外表面，永磁体靠近铜环的一侧温度高于其内表面的温度，铜环和永磁体最高温度分别达到248.79℃和122.06℃。

根据散热片结构参数优化仿真结果数据，分别绘制铜环、永磁体最高温度与散热片肋片高度、肋片厚度、底板厚度、肋片数量的关系曲线，如图6-图9所示。

图5 铜环和永磁体温度分布云图

图6 散热片肋片高度优化结果曲线

图7 散热片肋片厚度优化结果曲线

图8 散热片底板厚度优化结果曲线

图9 散热片肋片数量优化结果曲线

根据仿真结果曲线，在保证散热片结构机械强度的前提下，适量地增加散热片肋片高度、肋片厚度以及肋片数量都可以显著降低铜环和永磁体最高温度；而适当增加底板厚度可以降低铜环和永磁体的最高温度，但降低幅度较小。

4 结语

1) 永磁调速器运行时，会在铜环中持续产生涡旋状电流，这些涡电流产生的热量即为永磁调速器的发热热源。

2) 永磁调速器铜环上的温度呈现中间高两端低的趋势，且内表面温度略大于外表面，永磁体靠近铜环的一侧温度高于其内表面的温度。

3) 根据永磁调速器散热片仿真优化结果，合理选择肋片高度、肋片厚度、肋片数量的数值，可以显著降低永磁调速器各部件温度，这为散热片的结构优化提供了参考。