高速列车吊弦冲击动力特性的仿真研究

陈友均，阳光武，肖守讷，薛弼一，何春天

(西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

0 引言

列车的研发一直朝着高速、安全舒适的方向发展。高速列车大多使用电机牵引，采用这种方式时必须考虑供电系统的可靠性。由于吊弦的断裂导致供电故障的频繁发生，所用吊弦冲击载荷对列车行驶的安全性变得非常突出。轮轨关系和弓网耦合关系被法国、德国和日本等发达国家的科学家认为有着同样重要的位置。因此吊弦冲击动力的研究对于铁路运输有重要的意义[1]。

本文针对现有吊弦冲击动力研究中的不足，开展了弓网耦合机理下的吊弦动力学研究，通过建立高速弓网耦合动力学模型，对高速铁路吊弦冲击状态进行了动态仿真分析。

1 接触网结构类型和建模方法

国内外铁路接触网的悬挂结构形式基本上可分为如图 1所示的3种主要类型：(a)为德国采用的弹性链形悬挂，(b)为法国采用的简单链形悬挂，(c)为日本采用的复链形悬挂，其中图中的接触网两端和中间有图2所示的定位杆和腕臂支撑结构[2]。

图1 3种接触悬挂类型

图2 腕臂和定位器

1.1 接触网的数值建模方法

接触网的建模从最初的变刚度模型发展到现在的欧拉梁模型、张力弦模型、集中质量模型和与频率有关的有限元模型等，模型越来越复杂[3]。本文用2节点的欧拉伯努利梁模型对承力索和接触线进行建模。材料弯曲刚度，张力作用被考虑到承力索和接触线的建模中。

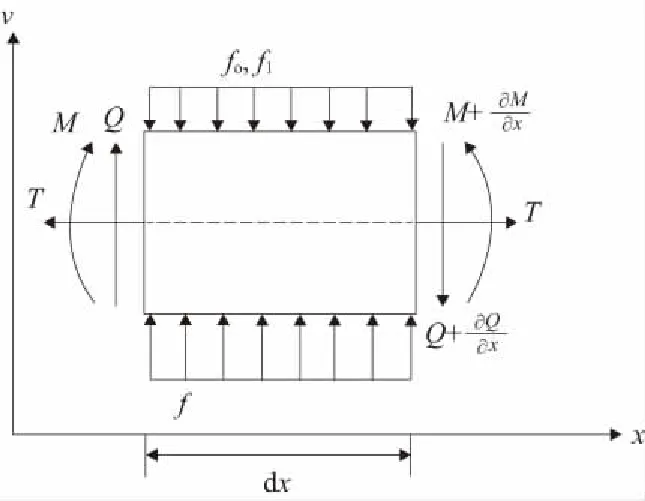
图3 接触线微段力和力矩平衡图

由力的平衡建立接触线微段的力平衡方程：

由力矩的平衡建立接触线微段的力矩平衡方程：

联立以上两式可得接触线微段的振动方程：

接触线假设近似平行，即斜率非常小，接触线两端的张紧力为恒定值，其中，ρc代表接触线的线密度，vc代表接触线相对平衡位置的位移，cc代表接触线阻尼值，EIc代表弯曲刚度，Tc代表张紧力，δ(x)代表x=0时的狄拉克函数，fre代表定位器的力，fdr代表吊弦的作用力，fc(t)代表弓网之间的接触力，ndrop代表吊弦的数量，nreg代表定位器的数量，xi代表第i根吊弦的位置，t和V分别代表列车的运行时间和车速。

1.2 接触网的有限元建模方法

在对接触网、吊弦和承力索进行数值分析建模时，因其结构复杂，在建模时，对接触网的实体结构在一定程度上进行简化。归算质量是受电弓的重要参数，因归算质量是根据动能相等的原理计算的，模型的简化会引起归算质量偏差，从而使线缆中能量传递的失真。为了消除这种简化的影响，让结果更加准确描述弓网接触和振动传递，把有限元模型运用到现实的仿真研究中来解决弓网之间的复杂耦合关系，并逐渐演化为全柔性弓网接触模型[5]。

本文根据接触网振动方程，接触网主要零部件所采用的单元类型如表 1所示。

表1 接触网主要零部件单元类型

在弓网之间建立接触时，为了避免在接触时出现负体积而使计算错误，在接触线的表面附加薄壳单元MAT 0，用于建立节点与节点间的接触。由于这种壳单元的厚度极薄，实际上在建立接触时，这种单元只起到连接作用，在仿真分析过程中不对结果产生影响。

根据吊弦线和承力索的实际工作情况，不具有线性拉压特性，且压缩刚度非常小，两端承受压缩载荷作用时不承受力的作用，所以用MATL 119这种单元来模拟吊弦和承力索是合适的，此外，这种单元可以根据试验数据分别定义加载和卸载曲线[6]。同时在进行显示动力学分析之前，初始重力会作用于大多数的结构中。重力作用响应时间在大刚度结构中可以不考虑，但对于索网结构，重力会对索网结构的初始形态产生影响。为减少重力对初始形态的影响[7]，本文在接触线受到受电弓作用前设置2 s虚加时间段，且为使在受电弓作用前，接触线能够达到平衡状态和悬挂高度在规定范围内，施加图4所示的接触线高度修正力。

图4所示为修正接触线悬挂高度前后接触悬挂点的高度示意图，虚线和实线分别为重力作用下施加修正力前后接触线形态。若以EN50318对接触线施工质量进行评价，接触线高度范围如表 2所示。

图4 吊弦位置预配修正

表2 接触线导高允许几何偏差表 单位：mm

参数接触网(250 km/h)接触网(300 km/h)接触线高度±30±30定位高度差±20±20

图5是考虑支柱定位和弹性补偿条件下接触线的边界条件示意图，这也是进行有限元分析的起始条件。表3为承力索和接触线的弹性补偿力，另外应考虑图6所示吊弦的非线性张力伸长量的变化关系。

图5 简单链形悬挂

表3 接触线、承力索张力和单位长度质量

线索张力/N单位长度质量/(kg/m)承力索16 0001.07接触线20 0001.35

图6 吊弦非线性张力长度变化曲线图

2 受电弓的建模方法

受电弓实际弓网作用状态如图7所示，受电弓主要由上导杆、下导杆、上框架、下框架、滑板5个部分组成，一般采用归算质量模型。

图7 弓网作用实际作用图

将受电弓简化为二质量的受电弓，如图8所示。参考受电弓的设计参数，把受电弓的弓头、上框架和下框架等效为归算质量模型。

图8 二质量受电弓

根据图8可得到二质量的动力学方程：

本文所采用的受电弓质量块-弹簧-阻尼归算模型[8]，将参照EN50318中的标准参数,如表4所示。

表4 二质量受电弓参数

3 吊弦动力学仿真分析

根据弓网系统组合，利用系统质量的刚度关系，在LS-DYNA中建立接触网和受电弓的接触有限元动力学模型，如图9所示。

图9 接触有限元动力学模型示意图

受电弓通过受电弓框架连接在车顶，接触网在两端通过弹性定位器和腕臂连接在支柱两点。受电弓弓头碳滑板相对于接触网接触线是滑动接触系，其相对运动速度和摩擦力关系为ff=FD+(FS-FD)e-DC|v|，其中DC、FD和FS分别为指数衰减系数、动摩擦因数、静摩擦因数。当速度v提高的时候，ff=FD，即越接近于动摩擦力；而当v=0时，ff=FS，越接近于静摩擦力。以标准EN50318中给定的验证条件为基础，对该系统运行速度为250km/h的列车进行仿真验证得到结果如表5所示[4]。

表5 验证模型参数对比

3.1 受电弓-吊弦动态作用

图10为高铁某段采集到在受电弓作用下，接触线受冲击力作用的位移图。吊弦在受电弓与接触网相互作用时，受到了弓网冲击力的作用。受电弓在通过吊弦正下方之前，在垂直方向接触网有一定的位移，且在受电弓到达最下端时，接触线的垂向位移达到最大，此时心型钳环和线夹吊环可能会出现接触分离。当受电弓通过了吊弦下端时，由于张力和重力作用，引起吊环与钳环之间的冲击作用[9]。

图10 在标注稳定线高度下的吊弦冲击位移图

3.2 弹性链形悬挂的动态性能

由标准载荷试验中得出的吊弦冲击高度影响冲击力大小的猜想，现通过本文模型进行仿真验证。标准EN50318中规定弓网静态接触力分别为120N、60N和30N，此时在车辆运行速度为250km/h、弓头质量为7.2kg和接触线张紧力20000N,且条件不变化的情况下，通过改变弓网静态接触力来实现对于接触线抬升量的调整，并验证抬升量对于吊弦冲击力的大小有较为重要的影响和作用。分别以3号吊弦和5号吊弦为例提取其冲击力的变化。

图11为静态接触力为120N时的振动载荷图，由图看出3号吊弦先由轴向拉伸变为轴向压缩，且在压缩完成后随着接触线回落到起始位置，在0.23s时吊弦力达到最大，为191.5N，并随时间振动逐渐变小。

图11 3号吊弦振动载荷图(120 N)

图12为静态接触力为120N时的振动载荷图，由图看出5号吊弦先由轴向拉伸变为轴向压缩，且在压缩完成后随着接触线回落到起始位置，在0.44s时吊弦力达到最大，为141.2N，并随时间振动逐渐变小。

图12 5号吊弦振动载荷图(120 N)

图13为静态接触力为60N时的振动载荷图，由图看出3号吊弦先由轴向拉伸变为轴向压缩，且在压缩完成后随着接触线回落到起始位置，在0.23s时吊弦力达到最大，为135.3N，并随时间振动逐渐变小。

图13 3号吊弦振动载荷图(60 N)

图14为静态接触力为60N时的振动载荷图，由图看出5号吊弦先由轴向拉伸变为轴向压缩，且在压缩完成后随着接触线回落到起始位置，在0.44s时吊弦力达到最大，为125.0N，并随时间振动逐渐变小。

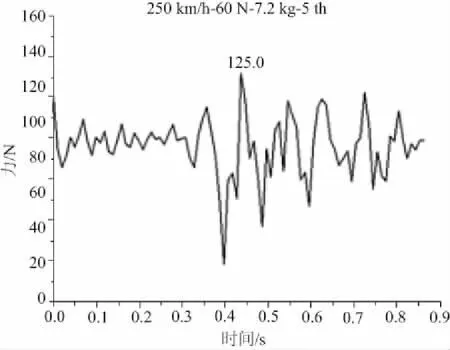
图14 5号吊弦振动载荷图(60 N)

图15为静态接触力为30N时的振动载荷图，由图看出3号吊弦先由轴向拉伸变为轴向压缩，且在压缩完成后随着接触线回落到起始位置，在0.23s时吊弦力达到最大，为103.6N，并随时间振动逐渐变小。

图15 3号吊弦振动载荷图(30 N)

图16为静态接触力为30N时的振动载荷图，由图看出5号吊弦先由轴向拉伸变为轴向压缩，且在压缩完成后随着接触线回落到起始位置，在0.44s时吊弦力达到最大，为115.3N，并随时间振动逐渐变小。

图16 5号吊弦振动载荷图(30 N)

由图17可看出随着弓网静态接触力的增大，吊弦下末端的抬升高度会随之增加，吊弦的冲击力也随之增大，此仿真所得到的结论和王伟[9]在台架试验得出的结论具有一致性，证明本文仿真结果的正确性。在本文所采用的弓网静态接触力的仿真范围内，吊弦所承受的最大冲击力值相对于静态接触力值呈线性增加的状态。由以上仿真结果可得静态接触力的增加会增加吊弦的抬升高度，从而增加吊弦最大冲击力的大小，且存在一定的线性关系。

图17 不同位置吊弦的冲击力

4 结语

通过参考解析数值分析方法中接触线和受电弓的定义分析方式，在软件LS-DYNA中建立起弓网接触作用的模型，并进行了吊弦的冲击载荷分析，能够得到以下结论：

1) 基于解析计算方法的弓网接触模型可以用于计算弓网的接触分析。

2) 随着静态接触力的减小，吊弦冲击力的变化范围明显变窄，峰值和谷值都在向静态轴向力附近靠近。

3) 通过对3种不同大小的静态接触力获得的吊弦冲击力进行对比，可知随着静态接触力的增大吊弦的冲击力也增大。