基于VB的喷气织机主喷嘴结构尺寸优化

钱晨，冯志华，赵冉

(苏州大学 机电工程学院，江苏 苏州 215021)

0 引言

在气流引纬的过程中，纱线在主喷嘴内高速气流的牵引下，由静态渐变为以一定速度轴向运动的近似稳态过程。因此，主喷嘴内部结构参数的大小影响着牵引纱线运动的流场分布，而通过改变主喷嘴内部结构的尺寸、形状来改善流场分布，提高引纬效率，近些年来国内外已有很多研究者做了深入的研究。冯志华、刘帅[1]在结构上提出了一种喷气型纺织机的主喷嘴模型和装配方法。董腾中等[2]基于FLUENT软件，对主喷嘴内部流场进行三维数值模拟并通过实验进行了验证。张科[3]将主喷嘴内部等直径导纱管改为锥形导纱管，研究了锥形导纱管两端直径比对内部流场的影响。路翔飞[4]对喷嘴芯不同抛物线方程、锥形套斜率等参数所形成的流场进行了研究。LIU Dingding等[5]利用正交实验法研究了喷嘴芯出口处外径、整流槽至喷嘴芯出口距离、喷嘴芯α面投影长度等参数对流场以及纱线牵引力的影响。CHEN Liang等[6]通过主喷嘴“串联”的结构形式分析了其内部流场的分布情况。LIU Shuai等[7-8]通过对纱线进行等离子处理，探究纱线表面特性与纱线所受阻力的响应关系。国外，VIKTOROV V等[9]结合流场数值计算和试验，对主喷嘴内流场的牵引力进行分析和评估。KERMANPUR A等[10]以工业实际数据为基础，利用人工神经网络算法，将喷嘴的不同喷射角度、垂直高度等参数对射流推力的影响做了相关的灵敏度分析。OYAMA. A等[11]通过将优化遗传算法与流体计算方程相结合，以轴流透平叶片的相关参数为设计变量，以熵为评价指标，开发了针对涡轮片结构设计的优化软件，在一定条件下得出了最优叶片以及最小熵损失量。

上述研究未能有效预估主喷嘴结构参数与纱线所受牵引力关系，也没有形成主喷嘴的具体优化方法。因此，本文对建立适用于ZAX型喷气织机主喷嘴结构的优化平台做了相关研究。具体而言，基于VB软件，将建模、流场分析、函数关系拟合和优化集成，以内部参数变为设计变量，一端固定纱线所受牵引力大小为设计目标，对主喷嘴内部结构尺寸优化，形成了一个较为完整的主喷嘴尺寸优化体系，极大地缩短了主喷嘴优化周期，提高了主喷嘴的引纬效率，同时也对工程类结构优化提供了一定的参考。

1 主喷嘴结构及流场模型

1.1 主喷嘴

ZAX型喷气织机主喷嘴是由喷嘴体、喷嘴芯、锥形套和加速导纱管组成。压缩空气从上端入口进入，通过内部结构腔，形成主喷嘴内部流场，牵引纱线向前作轴向运动。纱线在主喷嘴流场中运动受力模型如图1所示。

1—喷嘴芯；2—喷嘴体；3—锥形套；4—加速导纱管。图1 纱线在流体中运动受力模型

1.2 主喷嘴流场三维模型

基于上述主喷嘴结构，根据相关结构参数，通过ANSYS内置APDL语言对主喷嘴内部流场进行参数化建模。主要结构参数如下：喷嘴芯外端径向距离V4、喷嘴芯内孔半径V2、锥形套高度V3、环形气室径向高度V1、喉部长度H2、环形气室轴向长度H3等。主喷嘴内部流场三维模型以及相关结构变量分布如图2 所示。

图2 主喷嘴内部流场模型及设计变量

模型建立后，通过APDL命令流对其参数化划分网格。考虑流体模型结构的复杂以及流体仿真计算对网格精度的要求，以结构与非结构网格混合的形式对流场模型划分网格。流场网格模型如图3所示。

图3 主喷嘴流场网格模型

2 主喷嘴结构优化

本文在0.3MPa的供气压力下，通过单因素分析法，选取对纱线所受牵引力灵敏度影响较大的设计变量，并给定设计变量设计约束，通过优化算法求得最优设计参数组合以及对应的纱线所受最大牵引力。数学模型如式(1)所示。

(1)

鉴于VB软件可视化、模块化的编译优势，本文基于VB软件将主喷嘴内部流场建模、流场仿真计算、设计变量与设计目标关系的拟合以及遗传寻优等6个模块于VB中集成，生成.exe可执行文件。具体流程如图4所示。

图4 软件优化流程图

2.1 模型更改和流场计算

通过ANSYS中APDL命令流对流场模型参数化建模。首先，将参数化建模中的部分参数设定为变量，通过程序的循环迭代，实现相关结构参数的变化以及生成不同结构对应的.mac宏文件。其次，通过VB对ANSYS的调用，驱动ANSYS读取.mac宏文件，实现主喷嘴结构参数的变化、网格的划分和边界面的定义，并生成对应的.cdb网格文件，流程图如图5所示。最后通过FLUENT内置TUI语言，实现FLUENT对网格文件的读取、流体的参数化设置以及流体的仿真计算。与模型更改流程类似，在此不重复叙述。其中边界条件设置参考文献[4]。在流体计算收敛后输出中心轴线上的速度、密度等参数，图6为流场速度分布云图。

图5 模型更改流程图

图6 流场速度分布云图

2.2 数据处理

对流场计算输出的相关参数进行读取，根据文献[10]牵引力公式计算出纱线在不同主喷嘴流场中所受的牵引力大小。作用在纱线微元段上的牵引力如式(2)所示。

(2)

式中：Cf气流与纱线之间的摩擦因数；d为纱线直径；ρ气流密度；v为气流速度；u为纬纱飞行速度；dl为微段纱线长度。Cf是根据文献[12]，通过实验和仿真计算得出流场对不同纱线的牵引系数，例如OER13.5S型纱线牵引系数随相对速度变化及拟合曲线如图7所示。

图7 OER13.5S型纱线牵引系数随速度变化曲线

根据文献[13]，当气流速度超过50m/s时，纱线才能被顺利引纬。通过对原始流场结构模型仿真，分析中心轴线的速度分布，可大致得出所选取纱线的长度。根据以上参数和纱线所受牵引力公式可获得不同主喷嘴结构下纱线所受牵引力的大小。主喷嘴轴向速度分布如图8所示，纱线在不同入口气压下长度取值如表1所示。

图8 主喷嘴轴向速度分布图

表1 不同气压对应纱线长度表

气压P/MPa纱线长度L/m0.30.2670.40.2720.50.284

2.3 函数关系的拟合

通过编写拟合算法，以多元二次项形式拟合出设计变量与设计目标的函数关系。具体形式如式(3)所示。

(3)

其中:Ai、Bk、Ci、D为系数项，xi为设计变量。利用最小二乘法，构造新函数如式(4)所示。

(4)

2.4 遗传全局寻优

遗传算法寻优过程是模仿自然生物进行机制发展起来的随机全局搜索和优化方法。通过将设计变量的十进制数值转化为二进制初始种群，以适应度计算、选择、交叉和变异的方式来实现主喷嘴结构的优化，最后通过将输出的最优数据传递给模型更改模块来实现模型的更改，通过重复迭代计算，寻找设计变量最优参数组合。收敛标准如式(5)。

(5)

其中ε取值为0.01。最后输出最优参数组合以及最大牵引力值。图9为遗传算法流程图。

图9 遗传寻优流程图

3 优化结果分析

通过该软件的仿真优化，对28组不同结构参数的主喷嘴进行了数值模拟，计算出长度为0.267m的OER10.5S规格纱线在主喷嘴入口压力为0.3MPa的条件下所受的牵引力大小。

3.1 灵敏度的计算结果

通过单因素分析法，在约束区间内对设计变量做微小的变动，同时保持其他变量参数不变，进行仿真计算，计算得到相应的牵引力值大小，通过差分计算，得到各个变量对纱线所受牵引力的影响因子，如图10所示，分别为：V4、V2、V3、V1、H2。

图10 设计变量对牵引力灵敏度图

3.2 参数优化分析结果

表2给出了主喷嘴优化前后的结构参数和纱线所受牵引力大小。

表2 优化前后主喷嘴各参数对比

拟合设计点的牵引力大小与仿真计算值对比如图11、图12所示。

图11 牵引力拟合值与仿真计算值对比图

图12 牵引力拟合值与仿真计算值残差图

主喷嘴优化前后中性面流场速度云图如图13、图14所示。

图13 优化前流体中性面速度云图

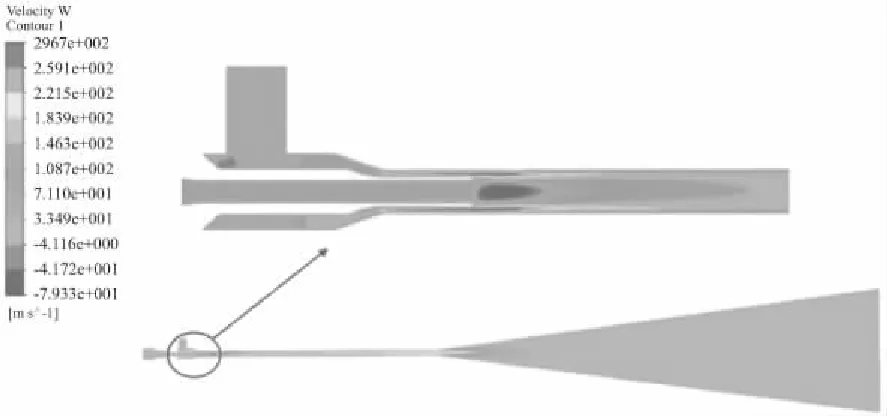
图14 优化后流体中性面速度云图

结合图15所示的优化前后主喷嘴内部流场中心轴线速度分布图可知：优化后主喷嘴环形气室的气流分布更为均匀，导纱管出口以及中心轴线的最大速度提高了2～5m/s，在负压区前端，中心轴线速度高了12m/s左右，且负速度区的长度缩减1.4mm。纱线在优化后主喷嘴中所受牵引力大小较优化前提高了10.6%。

图15 0.3 MPa下优化前后轴向中心速度对比图

综上所述，在V4=0.65mm、V2=0.90mm、V3=1.28mm、V1=1.32mm、H2=8.16mm的结构参数下，OER10.5S规格纱线所受最大牵引力fmax=0.291N。

4 实验验证

为了进一步验证此套优化理论以及优化结果的正确性，对优化前后主喷嘴进行实验验证。

4.1 材料准备

通过3D打印，打印出优化前后的主喷嘴，采用光敏树脂材质，打印精度为0.1mm，模型如图16所示。

图16 优化前后主喷嘴模型图

4.2 牵引力测量装置

装置主要由FD-1动态张力仪、BZ2210系列多通道动态电阻应变仪、DLF-3双通道电荷电压滤波积分放大器、INV高精度数据采集分析仪(图17、图18)组成。其中动态张力仪将收集到的应变信号传送到动态电阻应变仪，信号经过积分放大器的放大作用被数据采集仪接受并传到计算机设备。

图17 牵引力测试装置结构组成

图18 主喷嘴处局部放大图

4.3 实验测试结果分析

在主喷嘴入口压力为0.2～0.5MPa(增量为0.05MPa)下，对纱线进行牵引力测量，测量结果如图19所示：不同气压下，纱线所受牵引力的仿真值与实验值存在一定的误差，最大误差比为17.1%，但通过优化前后的喷嘴实验和仿真数据对比可知，在工况一定的条件下，不论是仿真计算还是实验测试，优化后的主喷嘴对应的纱线所受牵引力得到了提高。其中，仿真计算牵引力提高了10.6%，实验测量牵引力提高了6.4%，验证了优化的可靠性，提高了喷气织机的织布效率。

图19 主喷嘴优化前后纱线所受牵引力对比试验结果

5 结语

1) 基于VB平台，将参数化建模、流场数值模拟、函数关系拟合以及遗传寻优算法集成，编制出一套针对ZAX型喷气织机主喷嘴的优化算法,极大地提高了优化效率。

2) 通过灵敏度分析，确定了以喷嘴芯外端径向距离V4、喷嘴芯内孔半径V2、锥形套高度V3、环形气室径向高度V1、喉部长度H2为设计变量，以纱线所受牵引力为设计目标，在入口压力为0.3MPa下，得出了在一定设计约束条件下，主喷嘴的最优结构参数组合以及纱线所受最大牵引力值fmax。发现当V4=0.65mm、V2=0.90mm、V3=1.28mm、V1=1.32mm、H2=8.16mm时纱线所受牵引力fmax=0.291N。

3) 通过3D打印，将优化前后模型进行实验对比，验证了此套优化算法的可靠性和优化结果的正确性。其中，主喷嘴优化前后所测得纱线牵引力值与仿真计算所得值存在一定的误差，这是由于光敏树脂材质的主喷嘴内部较为粗糙，而仿真时流体与主喷嘴内表面为光滑接触，导致实验主喷嘴内部气流速度低于仿真流速，进而使得实验所测牵引力值小于仿真所得牵引力值。